北师大版七年级下册2 探索轴对称的性质课后练习题
展开(时间:30分钟)
一、选择题
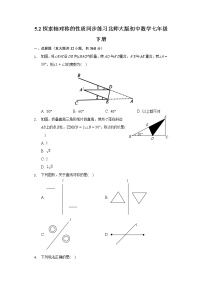
下列图形中,△A′B′C′与△ABC成轴对称的是( )
已知点A(a,1)与点B(5,b)关于y轴对称,则实数a,b的值分别是( )
A.5,1 B.﹣5,1 C.5,﹣1 D.﹣5,﹣1
若点A(m,n)和点B(5,﹣7)关于x轴对称,则m+n的值是( )
A.2 B.﹣2 C.12 D.﹣12
如下图是一台球桌面示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是( )
A.① B.② C.⑤ D.⑥
点P(﹣1,4)关于x轴对称的点P′的坐标是( )
A.(﹣1,﹣4) B.(-1,4) C.(1,﹣4) D.(1,4)
已知点P(1,a)与Q(b,2)关于x轴成轴对称,则a﹣b的值为( )
A.﹣1 B.1 C.﹣3 D.3
点P(x,y)在第二象限内,且|x|=2,|y|=3,则点P关于y轴的对称点的坐标为( )
A.(2,3) B.(﹣2,﹣3) C.(3,﹣2) D.(﹣3,2)
已知△ABC在平面直角坐标系中,点A,B,C都在第一象限内,现将△ABC的三个顶点的横坐标保持不变,纵坐标都乘﹣1,得到一个新的三角形,则( )
A.新三角形与△ABC关于x轴对称
B.新三角形与△ABC关于y轴对称
C.新三角形的三个顶点都在第三象限内
D.新三角形是由△ABC沿y轴向下平移一个单位长度得到的
下列说法正确的是( )
A.如果两个三角形全等,则它们是关于某条直线成轴对称的图形
B.如果两个三角形关于某条直线成轴对称,那么它们是全等三角形
C.等边三角形是关于一条边上的中线成轴对称的图形
D.一条线段是关于经过该线段中点的中线成轴对称的图形
如图,△ABC和△A′B′C′关于直线对称,下列结论中:
①△ABC≌△A′B′C′;
②∠BAC′=∠B′AC;
③l垂直平分CC′;
④直线BC和B′C′的交点不一定在l上,
正确的有( )
A.4个 B.3个 C.2个 D.1个
二、填空题
点E(a,-5)与点F(-2,b)关于y轴对称,则a= ,b= .
如图是某时刻在镜子中看到准确时钟的情况,则实际时间是
若点A(1﹣m,6)与B(2+n,6)关于某坐标轴对称,则m﹣n= .
如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有 个.
三、作图题
如图甲,正方形被划分成16个相同的三角形,将其中若干个三角形涂黑,且满足下列条件:
(1)涂黑部分的面积是原正方形面积的一半.
(2)涂黑部分成轴对称图形.
如图乙是一种涂法,请在图1~图3中分别设计另外三种涂法. (在所设计的图案中,若涂黑部分形状相同,则认为是同一种涂法,如图乙与图丙)
如图,已知A(2,3)、B(1,1)、C(4,1)是平面直角坐标系中的三点.
(1)请画出△ABC关于y轴对称的△A1B1C1;
(2)画出△A1B1C1向下平移3个单位得到的△A2B2C2;
(3)若△ABC中有一点P坐标为(x,y),请直接写出经过以上变换后△A2B2C2中点P的对应点P2的坐标.
\s 0 参考答案
B
答案为:B
答案为:C
答案为:B
A.
C
A.
答案为:A.
B
B
答案为:2,-5;
答案为:4:40.
答案为:3.
答案为:4.
解:根据轴对称图形的性质画图,但要注意本题中的要求涂黑部分的面积是原正方形面积的一半,所以图中一共有16个小三角形,那就要涂黑8个,而且这8个小三角形组成的图形要是轴对称图形.
不同涂法的图案举例如图:
解:(1)如图:△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求;
(3)根据题意可得点P2的坐标为(﹣x,y﹣3).
初中数学北师大版七年级下册2 探索轴对称的性质课堂检测: 这是一份初中数学北师大版七年级下册2 探索轴对称的性质课堂检测,共8页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
初中数学北师大版七年级下册第五章 生活中的轴对称2 探索轴对称的性质同步测试题: 这是一份初中数学北师大版七年级下册第五章 生活中的轴对称2 探索轴对称的性质同步测试题,共6页。试卷主要包含了如图,直线l,m相交于点O等内容,欢迎下载使用。
数学北师大版2 探索轴对称的性质优秀一课一练: 这是一份数学北师大版2 探索轴对称的性质优秀一课一练,共7页。试卷主要包含了2《探索轴对称的性质》,下列图形是轴对称图形的有,下列说法正确的是等内容,欢迎下载使用。