

- 2021年中考数学模拟测试卷(二) 试卷 1 次下载
- 2021年中考数学模拟测试卷(三) 试卷 1 次下载
- 2021年中考数学模拟测试卷(五) 试卷 1 次下载
- 2021年中考数学模拟测试卷(六) 试卷 0 次下载
- 2021年中考数学模拟测试卷(七) 试卷 0 次下载
2021年中考数学模拟测试卷(四)
展开2021年中考数学模拟测试卷(四)
一、选择题(每题4分,共40分)
1.-(-3) 的运算结果是 ( )
A.6 B. -6 C.9 D.-9
2.下列图形中,不可能是如图物体三视图中任何一种视图的是
(第2题)
A. B. C. D.
3.2020年5月22日,第十三届全国人大三次会议在北京胜利召开.《2020年政府工作报告》中显示,我国贫困人口减少1109万,贫困发生率降至0.6%,脱贫攻坚取得决定性成就.数据“1109万”用科学记数法表示为
A. B. 0.1 109 C. D.0.1 109
4.下列计算正确的是( )
A. B. C. D.
5.下列说法正确的是( )
A.要了解人们对“低碳生活”的了解程度,宜采用普查方式
B.一组数据3、4、5、5、6、7的众数和中位数都是5
C.随机事件的概率为50%,必然事件的概率为100%
D.若甲组数据的方差是0.168,乙组数据的方差是0.034,则甲组数据比乙组数据稳定
6.等腰三角形的两边长分别为3和6,则这个等腰三角形的周长为( )
A.12 B.15 C.12或15 D.18
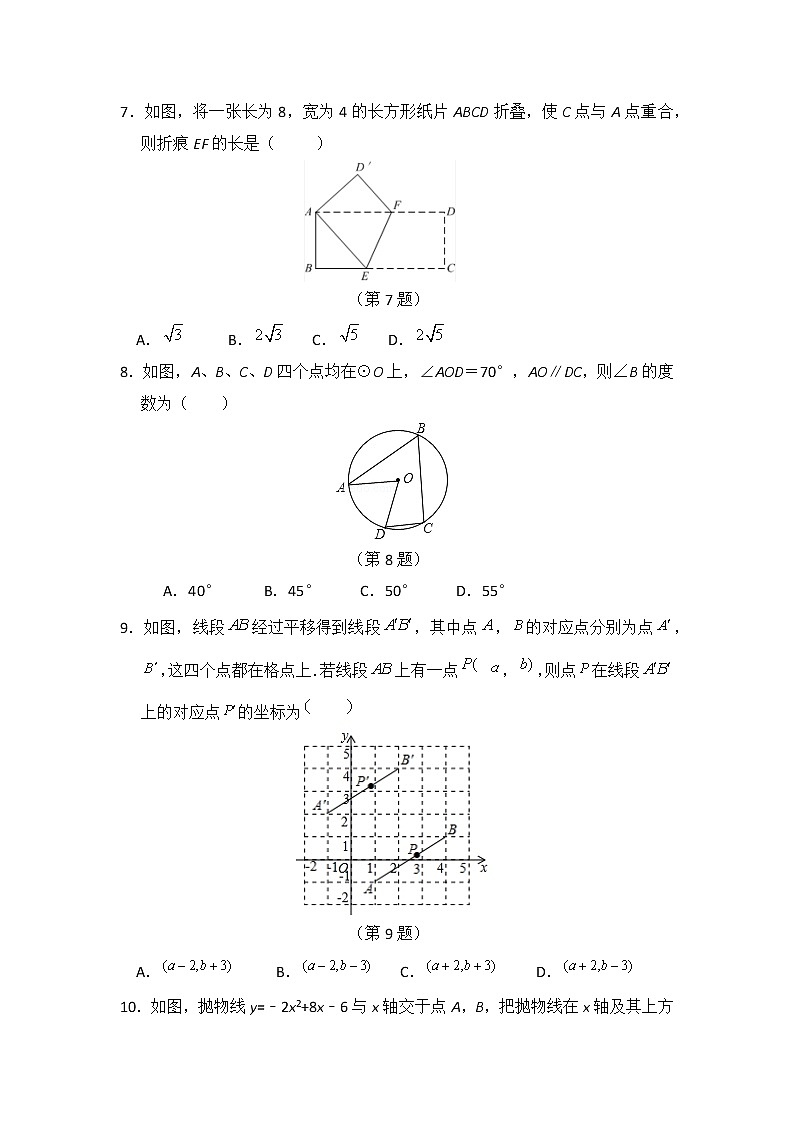
7.如图,将一张长为8,宽为4的长方形纸片ABCD折叠,使C点与A点重合,则折痕EF的长是( )
(第7题)
A. B. C. D.
8.如图,A、B、C、D四个点均在⊙O上,∠AOD=70°,AO∥DC,则∠B的度数为( )
(第8题)
A.40° B.45° C.50° D.55°
9.如图,线段经过平移得到线段,其中点,的对应点分别为点,,这四个点都在格点上.若线段上有一点 ,,则点在线段上的对应点的坐标为
(第9题)
A. B. C. D.
10.如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A,B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得到C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
(第10题)
A.﹣2<m<B.﹣3<m<﹣ C.﹣3<m<﹣2 D.﹣3<m<﹣
二、填空题(每题4分,共24分)
11.分解因式:__________.
12.学校总务处和教务处各领了同样数量的信封和信笺,总务处每发一封信都只用一张信笺,教务处每发一封信都用3张信笺,结果,总务处用掉了所有的信封,但余下50张信笺,而教务处用掉了所有的信笺,但余下50个信封,则两处各领的信笺张数,信封个数分别为__________.
13.若一个多边形的每一个外角都等于40°,则这个多边形的边数是__________.
14.如图,在正方形中,,,分别是边,上的点,且.与BE交于点,为的中点,则__________.
(第14题)
15.如图,在半径为2的⊙O中,两个顶点重合的内接正四边形与正六边形,则
阴影部分的面积为__________.
(第15题)
16.如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B 的坐标为(8,4),反比例函数y=(k>0)的图象分别交边BC,AB 于点D,E,连接DE,△DEF与△DEB关于直线DE对称,当点F恰好落在线段OA上时,则k的值是________.
(第16题)
三、解答题(共86分)
17.(8分)解不等式组 并写出整数解.
18.(8分)先化简,再求值:,其中是16的算术平方根.
19.(8分)已知:如图,∠ABC,射线BC上一点D,
求作:等腰三角形PBD,使线段BD为等腰三角形PBD的底边,点P在∠ABC的内部,且点P到∠ABC两边的距离相等.(不写作法,保留作图痕迹)
(第19题)
20.(8分)如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA长为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2,BF=2,求阴影部分的面积(结果保留π).
(第20题)
21.(8分)某区统计了有扶贫任务的人员一个月下乡扶贫的天数(为整数),并制成了如下尚不完整的表格与条形统计图(如图).
(第21题)
(1)有扶贫任务的人员的总人数是__________,并补全条形统计图;
(2)上级部门随机抽查1名扶贫人员,检查其工作情况,求抽查到的扶贫人员的扶贫天数大于7天的概率;
(3)若统计时漏掉1名扶贫人员,现将他的扶贫天数和原统计的扶贫天数合并成一组新数据后,发现平均数增大了,则漏掉的这名扶贫人员扶贫的天数最少是多少天.
22.(8分)某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量 (件)与每件销售价(元)之间的关系如下:
30 | 32 | 34 | 36 | |
40 | 36 | 32 | 28 |
(1)已知与满足一次函数关系,根据上表,求出与之间的关系式(不写出自变量的取值范围);
(2)如果该商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为(元),求出与之间的关系式,并求出每件商品销售价定为多少元时利润最大.
23.(10分)△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=
∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(第23题)
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;
(3)在(2)的条件下,BP=2,CQ=9,则BC的长为_______.
24.(12分)如图1,已知AB是⊙O的直径,AC是⊙O的弦,过O点作OF⊥AB交⊙O于点D,交AC于点E,交BC的延长线于点F,点G是EF的中点,连接CG.
(1)判断CG与⊙O的位置关系,并说明理由;
(2)求证:2OB2=BC•BF;
(3)如图2,当∠DCE=2∠F,CE=3,DG=2.5时,求DE的长.
(第24题)
25.(14分)如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.
(1)求出抛物线的解析式;
(2)在直线AC上方的抛物线上有一点D,使得△DCA的面积最大,求出点 D的坐标;
(3)P是直线x=1右侧的抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
答案
一、1. D 2.D 3.A 4.D 5.B
6. B 7.D 8.D 9.A 10. D
二、11. 12.150,100 13.9
14. 15. 6﹣2
16.12
三、17.解:
解不等式①,得x>2,
解不等式②,得x,
∴不等式组的解集是,∴其整数解是3、4、5、6.
18.解:原式
.
是16的算术平方根,
,
当时,原式.
19.解: 如图,三角形PBD即为所求作.
(第19题)
20.解:(1)BC与⊙O相切.
理由如下:如图,连接OD.
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD.
又∵OD=OA,
∴∠OAD=∠ODA.
∴∠CAD=∠ODA.
∴OD∥AC.
∴∠ODB=∠C=90°,即OD⊥BC.
又∵BC过半径OD的外端点D,
∴BC与⊙O相切.
(2)设OF=OD=x,则OB=OF+BF=x+2,
根据勾股定理得,OB2=OD2+BD2,即(x+2)2=x2+12,
解得x=2,即OD=OF=2,
∴OB=2+2=4,
∵在Rt△ODB中,OD=OB,
∴∠B=30°,
∴∠DOB=60°,
∴S扇形DOF==,
则阴影部分的面积为S△ODB﹣S扇形DOF=×2×2﹣ =2﹣ ,
故阴影部分的面积为2﹣ .
(第20题)
21.解:(1)100人;
补全条形统计图如图所示.
(第21题)
(2)∵有扶贫任务的人员一共有100人,其中扶贫天数大于7天的人员有15人,
∴P(抽查到的扶贫人员的扶贫天数大于7天).
(3)设漏掉的这名扶贫人员扶贫的天数为x天,根据题意得
,
解得.
∵x是整数,∴x的最小值为7.
∴漏掉的这名扶贫人员扶贫的天数最少是7天.
22.解:(1)设y与x之间的关系式为,根据题意得,解得故y与x之间的关系式为.
(2)根据题意得, ,解得,,故每件商品的销售价应定为35元或45元.
(3)由题意得,3 000,化为顶点式得,,故当时,取最大值,最大值为200,所以当每件商品销售价定为40元时利润最大.
23.(1)证明:∵△ABC是等腰直角三角形,
∴∠B=∠C=45°,AB=AC.
∵AP=AQ,
∴BP=CQ.
∵E是BC的中点,
∴BE=CE,
在△BPE和△CQE中,
∵,
∴△BPE≌△CQE(SAS).
(2)证明: 连接PQ,
∵△ABC和△DEF是两个全等的等腰直角三角形,
∴∠B=∠C=∠DEF=45°. ∵∠BEQ=∠EQC+∠C,
即∠BEP+∠DEF=∠EQC+∠C,
∴∠BEP+45°=∠EQC+45°,
∴∠BEP=∠EQC,
∴△BPE∽△CEQ.
(3) 6
24.(1)解:CG与⊙O相切,理由如下:
如图1,连接CE,
(第24题)
∵AB是⊙O的直径,
∴∠ACB=∠ACF=90°.
∵点G是EF的中点,
∴GF=GE=GC,
∴∠AEO=∠GEC=∠GCE.
∵OA=OC,
∴∠OCA=∠OAC.
∵OF⊥AB,
∴∠OAC+∠AEO=90°,
∴∠OCA+∠GCE=90°,即OC⊥GC.
∵OC是⊙O的半径,
∴CG与⊙O相切.
(2)证明:∵∠AOE=∠FCE=90°,∠AEO=∠FEC,
∴∠OAE=∠F.
又∵∠B=∠B,
∴△ABC∽△FBO,
∴,即BO•AB=BC•BF.
∵AB=2BO,
∴2OB2=BC•BF.
(3)解:由(1)知GC=GE=GF,
∴∠F=∠GCF,
∴∠EGC=2∠F.
又∵∠DCE=2∠F,
∴∠EGC=∠DCE.
∵∠DEC=∠CEG,
∴△ECD∽△EGC,
∴.
∵CE=3,DG=2.5,
∴,
整理,得DE2+2.5DE﹣9=0,
解得,DE=2或DE=﹣4.5(舍去),
故DE=2.
25.解:(1)∵该抛物线过点C(0,-2),
∴可设该抛物线的解析式为y=ax2+bx-2,将(4,0),(1,0)代入y=ax2+bx-2,
解得 ∴该抛物线的解析式为.
(2)如图,设D点的横坐标为t(0<t<4),则D点的纵坐标为
.
过D作y 轴的平行线交AC于E,由题意易得直线AC的解析式为 .
∴E点的坐标为
∴ .
∴ .
当t=2时,△DAC的面积最大, ∴D(2,1).
(3)存在,如图,设P点的横坐标为m,则P点的纵坐标为 .
当1<m<4时,AM=4-m, .
∵∠COA=∠PMA=90°,
∴①当时,△APM∽△ACO, 即 ,
解得m1=2,m2=4(舍去),∴P(2,1);
②当 时,△APM∽△CAO,即 ,
解得m3=4,m4=5(均不合题意,舍去),
∴当1<m<4时,P(2,1).
同理可求出当m>4时,P(5,-2);当m<1时,P(-3,-14),
综上所述,符合条件的点P的坐标为(2,1)或(5,-2)或(-3,-14).
(第25题)
2022年上海浦东第四教育署中考数学模拟预测试卷含解析: 这是一份2022年上海浦东第四教育署中考数学模拟预测试卷含解析
2022届四川省乐至县中考数学模拟预测试卷含解析: 这是一份2022届四川省乐至县中考数学模拟预测试卷含解析,共20页。试卷主要包含了考生要认真填写考场号和座位序号,下列哪一个是假命题,一、单选题,已知点A,下列各式中正确的是等内容,欢迎下载使用。
2022届四川广安市中考数学模拟预测试卷含解析: 这是一份2022届四川广安市中考数学模拟预测试卷含解析,共20页。试卷主要包含了下列说法错误的是,下列判断错误的是等内容,欢迎下载使用。












