2021年重庆市部分学校中考数学诊断试卷（3月份）

这是一份2021年重庆市部分学校中考数学诊断试卷（3月份），共39页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2021年重庆市部分学校中考数学诊断试卷（3月份）
一、选择题：（本大题12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑。
1．（4分）在下列“禁毒”、“和平”、“志愿者”、“节水”这四个标志中，属于轴对称图形的是（　　）
A． B．
C． D．
2．（4分）重庆是全国重点旅游城市，2020年实现旅游总收入约为57 400 000万元，数据57 400 000用科学记数法可表示
为（　　）
A．0.574×108 B．5.74×108 C．5.74×107 D．574×105
3．（4分）如图，已知△ABC与△DEF位似，位似中心为点O，且AB：DE＝3：2，则△ABC的面积与△DEF面积之比为（　　）

A．3：2 B．3：5 C．9：4 D．9：5
4．（4分）函数中，x的取值范围是（　　）
A．x＞﹣5 B．x＞﹣5且x≠0 C．x≥﹣5且x≠0 D．x≥﹣5
5．（4分）若x＝﹣1是关于x的一元二次方程ax2+bx﹣1＝0的一个根，则2021﹣2a+2b的值为（　　）
A．2019 B．2020 C．2022 D．2023
6．（4分）已知一次函数y＝kx+2的图象经过点A，且y随x的增大而减小，则点A的坐标可以是（　　）
A．（﹣1，2） B．（2，﹣1） C．（2，3） D．（3，4）
7．（4分）下列命题中，假命题是（　　）
A．对角线互相垂直的四边形是菱形
B．正方形的对角线互相垂直平分
C．矩形的对角线相等
D．对角线互相平分的四边形是平行四边形
8．（4分）如图，已知⊙O上三点A、B、C，连接AB、AC、OC，切线BD交OC的延长线于点D，若OC＝2，∠A＝30°，则DB的长为（　　）

A．4 B． C． D．1
9．（4分）A、B两地相距80km，甲、乙两人沿同一条路从A地到B地．l1，l2分别表示甲、乙两人离开A地的距离s（km）与时间t（h）之间的关系．对于以下说法：①乙车出发1.5小时后甲才出发；②两人相遇时，他们离开A地20km；③甲的速度是40km/h，乙的速度是km/h；④当乙车出发2小时时，两车相距13km．其中正确的结论是（　　）

A．①③ B．①④ C．②③ D．②④
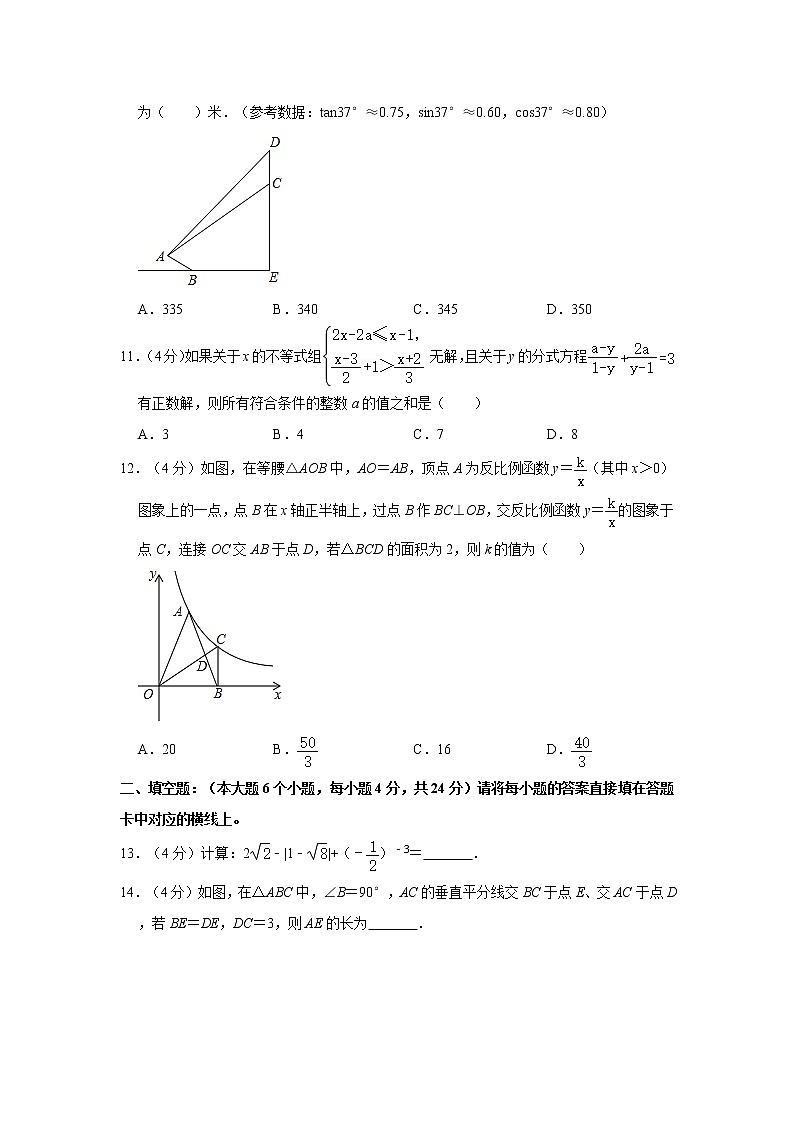
10．（4分）山城重庆的美景吸引了很多游客，越来越多的人喜欢用无人机拍摄网红景点．如图，为了拍摄坡比为1：2.4的斜坡AB上的景点A，航拍无人机先从C点俯拍，此时的俯角为37°，为取得更震撼的拍摄效果，无人机升高100米到达D点，此时的俯角变为45°．已知坡AB的长为65米，则无人机与斜坡AB的坡底B的水平距离BE的长度为（　　）米．（参考数据：tan37°≈0.75，sin37°≈0.60，cos37°≈0.80）

A．335 B．340 C．345 D．350
11．（4分）如果关于x的不等式组无解，且关于y的分式方程有正数解，则所有符合条件的整数a的值之和是（　　）
A．3 B．4 C．7 D．8
12．（4分）如图，在等腰△AOB中，AO＝AB，顶点A为反比例函数y＝（其中x＞0）图象上的一点，点B在x轴正半轴上，过点B作BC⊥OB，交反比例函数y＝的图象于点C，连接OC交AB于点D，若△BCD的面积为2，则k的值为（　　）

A．20 B． C．16 D．
二、填空题：（本大题6个小题，每小题4分，共24分）请将每小题的答案直接填在答题卡中对应的横线上。
13．（4分）计算：2﹣|1﹣|+（﹣）﹣3＝　 　．
14．（4分）如图，在△ABC中，∠B＝90°，AC的垂直平分线交BC于点E、交AC于点D，若BE＝DE，DC＝3，则AE的长为　 　．

15．（4分）现从﹣2，﹣，3中，任取两个不同的数分别作为二次函数y＝ax2﹣2x+b中的a和b，则所得抛物线与x轴有公共点的概率为　 　．
16．（4分）如图，在矩形ABCD中，AB＝3，AD＝2，以A为圆心，AD为半径作圆交AB于点E，F为的中点，过F作CD的平行线，交AD于点G，交BC于点H，则阴影部分的面积为　 　．

17．（4分）如图，在△ABC中，点D是线段AB上的一点，过点D作DE∥AC交BC于点E，将△BDE沿DE翻折，得到△B'DE，若点C恰好在线段B'D上，若∠BCD＝90°，DC：CB'＝3：2，AB＝16．则CE的长度为　 　．

18．（4分）元旦节前，某商店购进了一批A、B款式的大灯笼和若干小灯笼，其中小灯笼个数占灯笼总个数的80%，它们的进价之比为10：20：1，店主将三种灯笼分别加价50%、40%、100%进行销售，全部售完后利润率为54%．年关将至，该商店又购进了这三种灯笼，且进货量和之前分别相同，但是A、B款式的大灯笼进价分别上涨了50%、25%，小灯笼进价不变，于是店主将这两种大灯笼的价格分别在现在的进价基础上加价60%、40%进行销售，且购买一个A款式的大灯笼赠送两个小灯笼，购买一个B款式的大灯笼赠送4个小灯笼，余下的小灯笼售价与之前相同，那么这批灯笼卖完后，利润率为　 　．
三、解答题（本大题共6个小题，每题10分，共60分），解答时每小题都必须写出必要的演算过程或推理步骤，请将解答过程书写在答题卡中对应的位置上。
19．（10分）计算：
（1）（x﹣2y）2﹣x（x﹣4y）；
（2）+1．
20．（10分）目前，重庆市正全面开展生活垃圾分类工作．随着生活垃圾分类的全面推广，一些街镇也积极行动起来，通过入户宣传、开展各种趣味活动等，提高居民参与生活垃圾分类的积极性．为了进一步提高垃圾分类的准确度，某社区对甲、乙两个小区的居民进行了有关垃圾分类常识的测试，并从甲、乙两小区各随机抽取20名居民的测试成绩进行整理分析（成绩得分用x表示，共分成四组：A．10≤x＜15，B．15≤x＜20，C．20≤x＜25，D．25≤x≤30），下面给出了部分信息：
甲小区20名居民测试成绩：13，15，16，19，20，21，22，23，24，25，25，26，27，27，28，28，28，29，30，30．
乙小区20名居民测试成绩在C组中的数据是：20，23，21，24，22，21．
甲、乙两小区被抽取居民的测试成绩统计表

平均数
中位数
方差
甲小区
23.8
25
25.75
乙小区
22.3
b
24.34
根据以上信息，解答下列问题：
（1）a＝　 　，b＝　 　；
根据以上数据，你认为　 　小区（填“甲”或“乙”）垃圾分类的准确度更高，说明理由：　 　；
（2）若甲、乙两个校区居民共2400人，估计两个小区测试成绩优秀（x≥25）的居民人数是多少？

21．（10分）已知：在△ABC中，AB＝AC，BD⊥AC交AC于D．
（1）尺规作图：作线段BC的垂直平分线交BD于O，交BC于E，连接CO；
（2）若∠BAC＝56°，求∠DOC的度数．

22．（10分）学习函数时，我们经历了列表、描点、连线画出函数图象，观察分析图象特征，概括函数性质的过程．结合已有的学习经验，下面我们对函数的图象和性质进行探究，请将以下探究过程补充完整：
（1）选取适当的值补全表格；描点、连线，在所给的平面直角坐标系中画出函数的图象：
x
…
　 　
　 　
　 　
　 　
　 　
　 　
　 　
…
y
…
　 　
　 　
　 　
　 　
　 　
　 　
　 　
…

（2）结合图象，写出该函数的一条性质：　 　；
（3）结合这个函数的图象与性质，解决下列问题：
①若点A（x1，y1），B（x2，y2），C（x3，y3）在这个函数的图象上，且0＜x3＜3，﹣1＜x1＜x2＜0，请写出y1，y2，y3的大小关系：　 　（用“＜”连接）．
②若直线y＝2a+1（a是常数）与该函数图象有且只有三个交点，则a的取值范围为　 　．
23．（10分）在大力推广垃圾分类之前，某小区虽然在每栋楼都放置了可回收垃圾桶和不可回收垃圾桶，但是少数居民对垃圾分类的认识不够深入，常常将垃圾混装后随意丢入垃圾桶，导致垃圾分类混乱，垃圾处理站将可回收垃圾桶内的垃圾记为A类垃圾，将不可回收垃圾桶内的垃圾记为B类垃圾．该小区共有10栋楼，平均每栋楼每月产生12吨A类垃圾和4吨B类垃圾，每吨B类垃圾处理费是每吨A类垃圾处理费的2倍，该小区每月A、B两类垃圾处理费总费用为8000元．
（1）求每吨A类垃圾处理费多少元？
（2）在大力推广垃圾分类之后，该小区的居民认识到了垃圾分类的重要性并规范地放置垃圾．该小区每月产生的A、B两类垃圾总重量不变的情况下，B类垃圾的重量增加了a%，同时，垃圾处理站通过技术革新将A、B两类垃圾每吨处理费分别降低了a%和a%，这样与推广垃圾分类之前相比，该小区每月A、B两类垃圾处理费总费用减少了a%，求a的值．
24．（10分）如果一个三位数满足各位数字都不为0，且个位数字比十位数字大1，则称这个三位数为完美数．若m、n都是完美数，将组成m的各数位上的数字中最大数字作为两位数p的十位上的数字，组成n的各数位上的数字中最大数字作为两位数p的个位上的数字，再将组成m的各数位上的数字中最小数字作为两位数q的十位上的数字，组成n的各数位上的数字中最小数字作为两位数q的个位上的数字，所得的这两个数p、q之和记为F（m，n）．
例如：因为1+1＝2，4+1＝5，所以112和645都是完美数，则F（112，645）＝26+14＝40．
因为1+1＝2，8+1＝9，所以212和689都是完美数，则F（212，689）＝29+16＝45．
（1）判断623和456是否为完美数并说明原因．如果都是完美数则计算F（623，456）的值．
（2）若s、t都是完美数，其中s＝400+10x+y，t＝310+100a+b（1≤x≤8，1≤y≤9，0≤a≤5，1≤b≤9且x、y、a、b都是整数），规定：K（s，t）＝|s﹣t|，当F（s，123）﹣F（t，867）＝20时，求K（s，t）的最小值．
四、解答题：（本大题共2个小题，其中25题10分，26题8分，共18分）。解答时每小题都必须写出必要的演算过程或推理步骤，请将解答过程书写在答题卡中对应的位置上。
25．（10分）在平面直角坐标系中，抛物线y＝ax2+bx+c（a≠0）与x轴交于A，B两点（A在B的左侧），与y轴交于点C（0，6），其中AB＝8，tan∠CAB＝3．
（1）求抛物线的表达式；
（2）点P是直线BC上方抛物线上一点，过点P作PD∥AC交x轴于点D，交BC于点E，求BE的最大值及点P的坐标．
（3）将该抛物线沿射线CA方向平移2个单位长度得到抛物线y1，平移后的抛物线与原抛物线相交于点F，点G为抛物线y1的顶点，点M为直线FG上一点，点N为平面上一点．在（2）中，当BE的值最大时，是否存在以P、E、M、N为顶点的四边形是菱形，若存在，直接写出点N的坐标；若不存在，请说明理由．

26．（8分）如图，已知△ABC中，∠ABC＝45°，CD是边AB上的高线，E是AC上一点，连接BE，交CD于点F．
（1）如图1，若∠ABE＝15°，BC＝+1，求DF的长；
（2）如图2，若BF＝AC，过点D作DG⊥BE于点G，求证：BE＝CE+2DG；
（3）如图3，若R为射线BA上的一个动点，以BR为斜边向外作等腰直角△BRH，M为RH的中点．在（2）的条件下，将△CEF绕点C旋转，得到△CE'F'，E，F的对应点分别为E'，F'，直线MF'与直线AB交于点P，tan∠ACD＝，直接写出当MF'取最小值时的值．


2021年重庆市部分学校中考数学诊断试卷（3月份）
参考答案与试题解析
一、选择题：（本大题12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑。
1．（4分）在下列“禁毒”、“和平”、“志愿者”、“节水”这四个标志中，属于轴对称图形的是（　　）
A． B．
C． D．
【分析】根据轴对称图形的概念进行判断即可．
【解答】解：A、不是轴对称图形，故选项错误；
B、是轴对称图形，故选项正确；
C、不是轴对称图形，故选项错误；
D、不是轴对称图形，故选项错误．
故选：B．
2．（4分）重庆是全国重点旅游城市，2020年实现旅游总收入约为57 400 000万元，数据57 400 000用科学记数法可表示
为（　　）
A．0.574×108 B．5.74×108 C．5.74×107 D．574×105
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值＜1时，n是负整数．
【解答】解：57400000＝5.74×107．
故选：C．
3．（4分）如图，已知△ABC与△DEF位似，位似中心为点O，且AB：DE＝3：2，则△ABC的面积与△DEF面积之比为（　　）

A．3：2 B．3：5 C．9：4 D．9：5
【分析】利用位似的性质得到∴△ABC∽△DEF，然后根据相似三角形的性质求解．
【解答】解：∵△ABC与△DEF位似，位似中心为点O，
∴△ABC∽△DEF，
∴△ABC的面积与△DEF面积之比＝（）2＝（）2＝．
故选：C．
4．（4分）函数中，x的取值范围是（　　）
A．x＞﹣5 B．x＞﹣5且x≠0 C．x≥﹣5且x≠0 D．x≥﹣5
【分析】根据被开方数大于等于0，列式计算即可得解．
【解答】解：由题意得，x+5≥0，
解得x≥﹣5，
故选：D．
5．（4分）若x＝﹣1是关于x的一元二次方程ax2+bx﹣1＝0的一个根，则2021﹣2a+2b的值为（　　）
A．2019 B．2020 C．2022 D．2023
【分析】将x＝﹣1代入方程得出a﹣b＝1，再整体代入计算可得．
【解答】解：将x＝﹣1代入方程，得：a﹣b﹣1＝0，
则a﹣b＝1，
所以原式＝2021﹣2（a﹣b）
＝2021﹣2×1
＝2021﹣2
＝2019，
故选：A．
6．（4分）已知一次函数y＝kx+2的图象经过点A，且y随x的增大而减小，则点A的坐标可以是（　　）
A．（﹣1，2） B．（2，﹣1） C．（2，3） D．（3，4）
【分析】由y随x的增大而减小，利用一次函数的性质可得出k＜0，由各选项中点的坐标，利用一次函数图象上点的坐标特征可得出关于k的一元一次方程，解之即可得出k的值，取k值为负的选项即可得出结论．
【解答】解：∵y随x的增大而减小，
∴k＜0．
A、当点（﹣1，2）在一次函数y＝kx+2的图象上时，﹣k+2＝2，
解得：k＝0，选项A不符合题意；
B、当点（2，1）在一次函数y＝kx+2的图象上时，2k+2＝1，
解得：k＝﹣，选项B符合题意；
C、当点（2，3）在一次函数y＝kx+2的图象上时，2k+2＝3，
解得：k＝，选项C不符合题意；
D、当点（3，4）在一次函数y＝kx+2的图象上时，3k+2＝4，
解得：k＝，选项D不符合题意．
故选：B．
7．（4分）下列命题中，假命题是（　　）
A．对角线互相垂直的四边形是菱形
B．正方形的对角线互相垂直平分
C．矩形的对角线相等
D．对角线互相平分的四边形是平行四边形
【分析】对各个命题逐一判断后找到错误的即可确定假命题．
【解答】解：A、对角线互相垂直的平行四边形是菱形，原命题是假命题；
B、正方形的对角线互相垂直平分，是真命题；
C、矩形的对角线相等，是真命题；
D、对角线互相平分的四边形是平行四边形，是真命题；
故选：A．
8．（4分）如图，已知⊙O上三点A、B、C，连接AB、AC、OC，切线BD交OC的延长线于点D，若OC＝2，∠A＝30°，则DB的长为（　　）

A．4 B． C． D．1
【分析】连接OB，如图，根据切线的性质得∠OBD＝90°，再根据圆周角定理得到∠BOC＝60°，然后根据含30度的直角三角形三边的关系求BD的长．
【解答】解：连接OB，如图，
∵BD为切线，
∴OB⊥BD，
∴∠OBD＝90°，
∵∠BOC＝2∠A＝2×30°＝60°，
∴BD＝OB＝2．
故选：B．

9．（4分）A、B两地相距80km，甲、乙两人沿同一条路从A地到B地．l1，l2分别表示甲、乙两人离开A地的距离s（km）与时间t（h）之间的关系．对于以下说法：①乙车出发1.5小时后甲才出发；②两人相遇时，他们离开A地20km；③甲的速度是40km/h，乙的速度是km/h；④当乙车出发2小时时，两车相距13km．其中正确的结论是（　　）

A．①③ B．①④ C．②③ D．②④
【分析】根据题意和函数图象中的数据，可以判断各个小题中的结论是否正确，从而可以解答本题．
【解答】解：由图可得，
乙车出发1.5小时后甲已经出发一段时间，故①错误；
两人相遇时，他们离开A地20km，故②正确；
甲的速度是（80﹣20）÷（3﹣1.5）＝40（km/h），乙的速度是40÷3＝（km/h），故③正确；
当乙车出发2小时时，两车相距：[20+40×（2﹣1.5）]﹣×2＝（km），故④错误；
故选：C．
10．（4分）山城重庆的美景吸引了很多游客，越来越多的人喜欢用无人机拍摄网红景点．如图，为了拍摄坡比为1：2.4的斜坡AB上的景点A，航拍无人机先从C点俯拍，此时的俯角为37°，为取得更震撼的拍摄效果，无人机升高100米到达D点，此时的俯角变为45°．已知坡AB的长为65米，则无人机与斜坡AB的坡底B的水平距离BE的长度为（　　）米．（参考数据：tan37°≈0.75，sin37°≈0.60，cos37°≈0.80）

A．335 B．340 C．345 D．350
【分析】作AF⊥DE于点F，作AG⊥BE于点G，根据AB的坡比为1：2.4，AB的长为65米，可得AG＝15米，BG＝60米，设CF＝3x，AF＝4x，利用锐角三角函数即可求出结果．
【解答】解：如图，作AF⊥DE于点F，作AG⊥BE于点G，

由题意知：AB的坡比为1：2.4，AB的长为65米，
∴AG＝15米，BG＝60米，
∵AF⊥DE，AG⊥BE，BE⊥DE，
∴四边形AGEF是矩形，
∴EF＝AG＝15米，AF＝GE，
∵∠CAF＝37°，
∴tan∠CAF＝，
∴＝tan37°≈0.75＝，
设CF＝3x米，AF＝4x米，
在Rt△ADF中，∠DAF＝45°，CD＝100米，
∴AF＝DF，
∴4x＝3x+100，
解得x＝100，
∴GE＝AF＝4x＝400米，
∴BE＝GE﹣GB＝400﹣60＝340（米）．
故选：B．
11．（4分）如果关于x的不等式组无解，且关于y的分式方程有正数解，则所有符合条件的整数a的值之和是（　　）
A．3 B．4 C．7 D．8
【分析】先根据不等式组无解解出k的取值范围，再解分式方程得y＝，根据方程有解和非正整数解进行综合考虑k的取值，最后把这几个数相加即可．
【解答】解：∵不等式组无解，
∴2a﹣1≤7，
解得a≤4．
分式方程，
两边同时乘（y﹣1）得y﹣a+2a＝3（y﹣1），
解得y＝，
∵分式方程有正数解，
∴＞0且≠1，
解得a＞﹣3且a≠﹣1，
∴﹣3＜a≤4且a≠﹣1，
又∵a是整数，
∴a＝﹣2，0，1，2，3，4，
∴所有符合条件的整数a的值之和是﹣2+0+1+2+3+4＝8．
故选：D．
12．（4分）如图，在等腰△AOB中，AO＝AB，顶点A为反比例函数y＝（其中x＞0）图象上的一点，点B在x轴正半轴上，过点B作BC⊥OB，交反比例函数y＝的图象于点C，连接OC交AB于点D，若△BCD的面积为2，则k的值为（　　）

A．20 B． C．16 D．
【分析】过点A作AF⊥OB交x轴于F，交OC于点E，利用等腰三角形性质可得OF＝FB＝OB，再由AF∥BC，可得△ADE∽△BDC，BC＝2EF，设OF＝a，则OB＝2a，可得AF＝2BC＝4EF，AE＝3EF，应用相似三角形性质及三角形面积可由△BCD的面积为2，求得△AOF的面积，应用|k|的几何意义求k．
【解答】解：如图，过点A作AF⊥OB交x轴于F，交OC于点E，
∵OA＝AB，AF⊥OB，
∴OF＝FB＝OB，
∵BC⊥OB，
∴AF∥BC，
∴△ADE∽△BDC，＝＝＝，
∴BC＝2EF，
设OF＝a，则OB＝2a，
∴A（a，），C（2a，），
∴AF＝，BC＝，
∴AF＝2BC＝4EF，AE＝AF﹣EF＝3EF，
∵△ADE∽△BDC，
∴＝＝＝，
∴＝＝，
∵△BCD的面积为2，
∴S△ADE＝，
∴＝，
∵＝，
∴EC＝OE，
∴＝，
∴＝，
∴S△AOE＝，
∵＝＝，
∴＝＝，
∴S△AOF＝S△AOE＝×＝10，
∴＝10，
∵k＞0，
∴k＝20．
故选：A．

二、填空题：（本大题6个小题，每小题4分，共24分）请将每小题的答案直接填在答题卡中对应的横线上。
13．（4分）计算：2﹣|1﹣|+（﹣）﹣3＝　﹣7　．
【分析】直接利用绝对值的性质以及负整数指数幂的性质分别化简得出答案．
【解答】解：原式＝2﹣（2﹣1）﹣8
＝2﹣2+1﹣8
＝﹣7．
故答案为：﹣7．
14．（4分）如图，在△ABC中，∠B＝90°，AC的垂直平分线交BC于点E、交AC于点D，若BE＝DE，DC＝3，则AE的长为　2　．

【分析】根据线段垂直平分线的性质得到EA＝EC，根据角平分线的判定定理得到∠EAC＝∠BAE，得到∠EAC＝∠C＝∠BAE＝30°，根据余弦的定义计算，得到答案．
【解答】解：∵DE是线段AC的垂直平分线，
∴EA＝EC，
∴∠EAC＝∠C，
∵BE＝DE，∠B＝90°，ED⊥AC，
∴∠EAC＝∠BAE，
∴∠EAC＝∠C＝∠BAE＝30°，
在Rt△CED中，EC＝＝2，
∴AE＝2，
故答案为：2．
15．（4分）现从﹣2，﹣，3中，任取两个不同的数分别作为二次函数y＝ax2﹣2x+b中的a和b，则所得抛物线与x轴有公共点的概率为　　．
【分析】画树状图展示所有12种等可能的结果数，利用二次函数的性质，找出抛物线y＝ax2﹣2x+b与x轴有公共点的个数，然后根据概率公式即可得出答案．
【解答】解：﹣＝﹣0.5，＝0.5，根据题意画图如下：
，
共有12种等情况数，其中抛物线y＝ax2﹣2x+b与x轴有公共点（4﹣4ab≥0，即ab≤1）的有10种情况，
则抛物线y＝ax2﹣2x+b与x轴有公共点的概率为＝，
故答案为：．
16．（4分）如图，在矩形ABCD中，AB＝3，AD＝2，以A为圆心，AD为半径作圆交AB于点E，F为的中点，过F作CD的平行线，交AD于点G，交BC于点H，则阴影部分的面积为　3﹣2　．

【分析】根据题意求得△AMF是等腰直角三角形，即可求得AM＝FM＝，从而求得BM＝3﹣，然后根据阴影部分的面积＝矩形BMFH的面积求得即可．
【解答】解：连接AF，作FM⊥AB于M，
∵F为的中点，
∴∠DAF＝∠EAF＝45°，
∴∠AFM＝90°﹣45°＝45°，
∴∠FAM＝∠AFM，
∴AM＝FM，
∵AF＝AD＝2，
∴FM＝AM＝×2＝，
∴BM＝3﹣，
∴S阴影＝BM•FM＝（3﹣）•＝3﹣2，
故答案为3﹣2．

17．（4分）如图，在△ABC中，点D是线段AB上的一点，过点D作DE∥AC交BC于点E，将△BDE沿DE翻折，得到△B'DE，若点C恰好在线段B'D上，若∠BCD＝90°，DC：CB'＝3：2，AB＝16．则CE的长度为　3　．

【分析】设DC＝3x，CB＝2x，则DB'＝5x，由折叠的性质得出DB＝DB'，∠BDE＝∠B'DE，BE＝B'E，由勾股定理求出BC＝8，设CE＝a，则BE＝8﹣a＝B'E，由勾股定理得出方程求出a的值，则可得出答案．
【解答】解：设DC＝3x，CB'＝2x，则DB'＝5x，
∵将△BDE沿DE翻折，得到△B'DE，
∴DB'＝DB，∠BDE＝∠B'DE，BE＝B'E，
∵DE∥AC，
∴∠A＝∠BDE，∠ACD＝∠CDE，
∴∠A＝∠ACD，
∴CD＝AD＝3x，
∴AB＝AD+DB＝8x＝16，
∴x＝2，
∴CD＝6，BD＝10，B'C＝4，
∴BC＝＝8，
设CE＝a，则BE＝8﹣a＝B'E，
∵CE2+B'C2＝B'E2，
∴，
解得a＝3，
∴CE＝3，
故答案为：3．
18．（4分）元旦节前，某商店购进了一批A、B款式的大灯笼和若干小灯笼，其中小灯笼个数占灯笼总个数的80%，它们的进价之比为10：20：1，店主将三种灯笼分别加价50%、40%、100%进行销售，全部售完后利润率为54%．年关将至，该商店又购进了这三种灯笼，且进货量和之前分别相同，但是A、B款式的大灯笼进价分别上涨了50%、25%，小灯笼进价不变，于是店主将这两种大灯笼的价格分别在现在的进价基础上加价60%、40%进行销售，且购买一个A款式的大灯笼赠送两个小灯笼，购买一个B款式的大灯笼赠送4个小灯笼，余下的小灯笼售价与之前相同，那么这批灯笼卖完后，利润率为　41.6%　．
【分析】首先根据题意得出c与a，b的关系，然后根据利润率的公式求出a与b的关系，最后根据第二次销售列出利润率，然后把之前得到的两个式子代入即可得到结果．
【解答】解：设A款打灯笼有a个，B款大灯笼由b个，小灯笼有c个，
则由题意得：c＝（a+b+c）×0.8，
即c＝4（a+b）①，
设它们的进价分别为10y，20y，y，
由题意得：＝54%，
将c＝4（a+b）代入得：a＝b②，
在第二次购买销售中，由题意得，
它们的进价为：15y，25y，y，
利润率＝
将①，②代入上式得：
利润率＝41.6%．
故答案为：41.6%．
三、解答题（本大题共6个小题，每题10分，共60分），解答时每小题都必须写出必要的演算过程或推理步骤，请将解答过程书写在答题卡中对应的位置上。
19．（10分）计算：
（1）（x﹣2y）2﹣x（x﹣4y）；
（2）+1．
【分析】（1）先乘方再乘法，最后合并同类项；
（2）把 a﹣3 看成分母为 1 的分数，通分后与 相乘，化为最简分式后再加1．
【解答】解：（1）原式＝x2﹣4xy+4y2﹣x2+4xy
＝4y2；
（2）原式＝
＝
＝
＝
＝
＝
＝
＝．
20．（10分）目前，重庆市正全面开展生活垃圾分类工作．随着生活垃圾分类的全面推广，一些街镇也积极行动起来，通过入户宣传、开展各种趣味活动等，提高居民参与生活垃圾分类的积极性．为了进一步提高垃圾分类的准确度，某社区对甲、乙两个小区的居民进行了有关垃圾分类常识的测试，并从甲、乙两小区各随机抽取20名居民的测试成绩进行整理分析（成绩得分用x表示，共分成四组：A．10≤x＜15，B．15≤x＜20，C．20≤x＜25，D．25≤x≤30），下面给出了部分信息：
甲小区20名居民测试成绩：13，15，16，19，20，21，22，23，24，25，25，26，27，27，28，28，28，29，30，30．
乙小区20名居民测试成绩在C组中的数据是：20，23，21，24，22，21．
甲、乙两小区被抽取居民的测试成绩统计表

平均数
中位数
方差
甲小区
23.8
25
25.75
乙小区
22.3
b
24.34
根据以上信息，解答下列问题：
（1）a＝　40　，b＝　22.5　；
根据以上数据，你认为　甲　小区（填“甲”或“乙”）垃圾分类的准确度更高，说明理由：　甲小区垃圾分类的平均数及中位数均大于乙小区，所以甲社区的平均成绩高且高分人数多　；
（2）若甲、乙两个校区居民共2400人，估计两个小区测试成绩优秀（x≥25）的居民人数是多少？

【分析】（1）先求出乙社区C组人数，再根据百分比之和为1求出a的值，根据中位数的定义可得b的值，从平均数和中位数的意义分析可知哪个社区更好；
（2）用总人数乘以样本中成绩优秀的人数和占甲、乙社区人数之和的比例即可．
【解答】解：（1）乙小区20名居民测试成绩在C组中的数据所占百分比为6÷20×100%＝30%，
∴a＝100﹣10﹣20﹣30＝40，
A、B组数据的个数为20×（10%+20%）＝6，
其中位数为＝22.5，即b＝22.5；
根据以上数据，认为甲小区垃圾分类的准确度更高，理由如下：
甲小区垃圾分类的平均数及中位数均大于乙小区，所以甲社区的平均成绩高且高分人数多，
故答案为：40、22.5，甲、甲小区垃圾分类的平均数及中位数均大于乙小区，所以甲社区的平均成绩高且高分人数多；
（2）估计两个小区测试成绩优秀（x≥25）的居民人数是2400×＝1140（人）．
21．（10分）已知：在△ABC中，AB＝AC，BD⊥AC交AC于D．
（1）尺规作图：作线段BC的垂直平分线交BD于O，交BC于E，连接CO；
（2）若∠BAC＝56°，求∠DOC的度数．

【分析】（1）利用基本作图作BC的垂直平分线；
（2）根据线段垂直平分线的性质得到点A、O、E共线，OB＝OC，再利用等腰三角形的性质和等腰三角形的性质得∠ABC＝∠C＝62°，接着利用互余计算出∠DBC＝28°，然后根据等腰三角形的性质和三角形外角性质计算∠DOC的度数．
【解答】解：（1）如图，点O、E为所作；

（2）∵AB＝AC，OE垂直平分BC，
∴点A、O、E共线，OB＝OC，
∵AB＝AC，
∴∠ABC＝∠C＝（180°﹣∠BAC）＝（180°﹣56°）＝62°，
∵BD⊥AC，
∴∠ODC＝90°，
∴∠DBC＝90°﹣62°＝28°，
∵OB＝OC，
∴∠OBC＝∠OCB＝28°，
∴∠DOC＝∠OBC+∠OCB＝56°．
22．（10分）学习函数时，我们经历了列表、描点、连线画出函数图象，观察分析图象特征，概括函数性质的过程．结合已有的学习经验，下面我们对函数的图象和性质进行探究，请将以下探究过程补充完整：
（1）选取适当的值补全表格；描点、连线，在所给的平面直角坐标系中画出函数的图象：
x
…
　﹣3　
　﹣2　
　﹣1　
　0　
　1　
　2　
　3　
…
y
…
　　
　1　
　2　
　2　
　0　
　﹣2　
　2　
…

（2）结合图象，写出该函数的一条性质：　当x＜0时，y随x增大而增大　；
（3）结合这个函数的图象与性质，解决下列问题：
①若点A（x1，y1），B（x2，y2），C（x3，y3）在这个函数的图象上，且0＜x3＜3，﹣1＜x1＜x2＜0，请写出y1，y2，y3的大小关系：　y3＜y1＜y2　（用“＜”连接）．
②若直线y＝2a+1（a是常数）与该函数图象有且只有三个交点，则a的取值范围为　　．
【分析】（1）取x的值，代入相应的式子计算即可得对应y值，由表描点连线即为图象；
（2）从增减性或最值描述函数的性质即可；
（3）数形结合即可得到答案．
【解答】解：（1）列表如下表所示：

图象如图所示：

（2）当x＜0时，y随x增大而增大；当x＞2时，y随x增大而增大（答案不唯一）；
（3）①数形结合可知y3＜y1＜y2，
故答案为：y3＜y1＜y2．
②数形结合可知0＜2a+1≤2，
解得，
故答案为．
23．（10分）在大力推广垃圾分类之前，某小区虽然在每栋楼都放置了可回收垃圾桶和不可回收垃圾桶，但是少数居民对垃圾分类的认识不够深入，常常将垃圾混装后随意丢入垃圾桶，导致垃圾分类混乱，垃圾处理站将可回收垃圾桶内的垃圾记为A类垃圾，将不可回收垃圾桶内的垃圾记为B类垃圾．该小区共有10栋楼，平均每栋楼每月产生12吨A类垃圾和4吨B类垃圾，每吨B类垃圾处理费是每吨A类垃圾处理费的2倍，该小区每月A、B两类垃圾处理费总费用为8000元．
（1）求每吨A类垃圾处理费多少元？
（2）在大力推广垃圾分类之后，该小区的居民认识到了垃圾分类的重要性并规范地放置垃圾．该小区每月产生的A、B两类垃圾总重量不变的情况下，B类垃圾的重量增加了a%，同时，垃圾处理站通过技术革新将A、B两类垃圾每吨处理费分别降低了a%和a%，这样与推广垃圾分类之前相比，该小区每月A、B两类垃圾处理费总费用减少了a%，求a的值．
【分析】（1）每吨A类垃圾处理费为x元，则每吨B类垃圾处理费为2x元，根据该小区每月A、B两类垃圾处理总费用为8000元，即可得出关于x的一元一次方程，解之即可得出结论；
（2）根据处理垃圾的总费用＝每吨垃圾的处理费用×该类垃圾的吨数，即可得出关于a的一元二次方程，解之取其正值即可得出结论．
【解答】解：（1）设每吨A类垃圾处理费为x元，则每吨B类垃圾处理费为2x元，
依题意，得：10×（12x+4×2x）＝8000，
解得：x＝40．
答：每吨A类垃圾处理费为40元．
（2）依题意，得：40（1﹣a%）×10×[12+4﹣4（1+a%）]+40×2（1﹣a%）×10×4（1+a%）＝8000（1﹣a%），
整理，得：2a﹣0.05a2＝0，
解得：a1＝40，a2＝0（不合题意，舍去）．
答：a的值为40．
24．（10分）如果一个三位数满足各位数字都不为0，且个位数字比十位数字大1，则称这个三位数为完美数．若m、n都是完美数，将组成m的各数位上的数字中最大数字作为两位数p的十位上的数字，组成n的各数位上的数字中最大数字作为两位数p的个位上的数字，再将组成m的各数位上的数字中最小数字作为两位数q的十位上的数字，组成n的各数位上的数字中最小数字作为两位数q的个位上的数字，所得的这两个数p、q之和记为F（m，n）．
例如：因为1+1＝2，4+1＝5，所以112和645都是完美数，则F（112，645）＝26+14＝40．
因为1+1＝2，8+1＝9，所以212和689都是完美数，则F（212，689）＝29+16＝45．
（1）判断623和456是否为完美数并说明原因．如果都是完美数则计算F（623，456）的值．
（2）若s、t都是完美数，其中s＝400+10x+y，t＝310+100a+b（1≤x≤8，1≤y≤9，0≤a≤5，1≤b≤9且x、y、a、b都是整数），规定：K（s，t）＝|s﹣t|，当F（s，123）﹣F（t，867）＝20时，求K（s，t）的最小值．
【分析】（1）根据新定义列算式．
（2）根据新定义可以确定b的值及x、y的等量关系．当F（s，123）﹣F（t，867）＝20，确定出x与a的等量关系，然后根据新定义K（s，t）＝|s﹣t|，求出x的取值范围，即可求出最后的值．
【解答】解：（1）∵2+1＝3，5+1＝6，
∴623和456是完美数，
∴F（623，456）＝66+24＝90．
答：623和456是完美数，
F（623，456）的值为90．
（2）∵s＝400+10x+y，y＝x+1，
t＝310+100a+b，b＝1+1＝2．
∴K（s，t）＝|s﹣t|＝|400+10x+x+1﹣310﹣100a﹣2|
＝|89+11x﹣100a|，
①当x≥4时，F（s，123）＝10y+3+41
＝10（x+1）+44
＝10x+54．
F（t，867）＝10（a+3）+8+16，
＝10a+54．
∵F（s，123）﹣F（t，867）＝20，
∴10x+54﹣（10a+54）＝10x﹣10a＝20．
∴x＝a+2．
即K（s，t）＝|s﹣t|
＝|89+11x﹣100a|
＝|89+11x﹣100（x﹣2）|
＝|289﹣89x|，
又∵4≤x≤8，
∴K（s，t）的最小值为|289﹣89×4|＝67．
②当x＜4时，
F（s，123）＝43+10x+1
＝10x+44，
F（t，867）＝10（a+3）+8+16
＝10a+54．
∵F（s，123）﹣F（t，867）＝20，
∴10x+44﹣（10a+54）＝20，
解得x＝a+3．
∴K（s，t）＝|89+11x﹣100（a+3）|
＝|389﹣89x|，
∵1≤x＜4，
∴K（s，t）的最小值为|389﹣89×1|＝300．
综上所述最小值为67．
答：K（s，t）的最小值为67．
四、解答题：（本大题共2个小题，其中25题10分，26题8分，共18分）。解答时每小题都必须写出必要的演算过程或推理步骤，请将解答过程书写在答题卡中对应的位置上。
25．（10分）在平面直角坐标系中，抛物线y＝ax2+bx+c（a≠0）与x轴交于A，B两点（A在B的左侧），与y轴交于点C（0，6），其中AB＝8，tan∠CAB＝3．
（1）求抛物线的表达式；
（2）点P是直线BC上方抛物线上一点，过点P作PD∥AC交x轴于点D，交BC于点E，求BE的最大值及点P的坐标．
（3）将该抛物线沿射线CA方向平移2个单位长度得到抛物线y1，平移后的抛物线与原抛物线相交于点F，点G为抛物线y1的顶点，点M为直线FG上一点，点N为平面上一点．在（2）中，当BE的值最大时，是否存在以P、E、M、N为顶点的四边形是菱形，若存在，直接写出点N的坐标；若不存在，请说明理由．

【分析】（1）由C（0，6），tan∠CAB＝3，求出OA的长度，确定点A、点B的坐标，再用待定系数法求抛物线的表达式；
（2）先求直线AC、BC的表达式，再设点P的横坐标为m，由PD∥AC求出直线PD的表达式，与直线BC的表达式组成方程组，求出点E的坐标，再用含字母m的式子表示BE，根据二次函数的性质求出BE的最大值及点P的坐标；
（3）先根据△AOC沿射线CA方向平移2个单位后的位置，确定抛物线y1的表达式及顶点G和点F的坐标，求出直线FG的函数表达式，再根据（2）中求出的点P的坐标求出点E的坐标，按照PE为边、对角线等情况画出相应的菱形，求出点N的坐标．
【解答】解：（1）∵C（0，6），＝tan∠CAB＝3，
∴AO＝＝2，A（﹣2，0），B（6，0），
∴，解得，
∴该抛物线的表达式为y＝x2+2x+6．
（2）如图1，作PH⊥x轴于点H，交BC于点J，作EI⊥PH于点I、EK⊥x轴于点K．
设直线BC的函数表达式为y＝kx+6，则6k+6＝0，解得k＝﹣1，
∴y＝﹣x+6；
设直线AC的函数表达式为y＝px+6，则﹣2p+6＝0，解得p＝3，
∴y＝3x+6．
设P（m，m2+2m+6），由PD∥AC，设直线PD的函数表达式为y＝3x+n，
则m2+2m+6＝3m+n，解得n＝m2﹣m+6，
∴y＝3xm2﹣m+6．
由，得，
∴E（，）．
∵AC＝＝2，BC＝＝6，且△PEI∽△CAO，△BEK∽△BCO，
∴EI：PI：PE＝OA：OC：AC＝1：3：，EK：BK：BE＝CO：BO：BC＝1：1：，
∴PE＝EI，
∴PE＝10EI＝10（m﹣﹣）＝m﹣m2，
∵BE＝BK，
∴BE＝2BK＝2（6﹣﹣）＝12﹣﹣，
∴BE＝m﹣m2﹣（12﹣﹣）＝﹣m2+8m﹣12＝﹣（m﹣4）2+4，
∴当m＝4时，BE的最大值，最大值为4，此时P（4，6）．

（3）存在．
如图2，由（2）得，AC＝2，将△AOC沿射线CA方向平移2个单位，相当于将△AOC向左平移2个单位，再向下平移6个单位，
∴该抛物线也向左平移2个单位，再向下平移6个单位，
∵原抛物线为y＝x2+2x+6＝（x﹣2）2+8，
∴y1＝x2+2，抛物线y1与坐标轴的交点分别为F（﹣2，0）、D'（2，）、（0，2），且顶点为G（0，2），点F（﹣2，0）为抛物线y1与原抛物线的交点．
∵P（4，6），C（0，6），且PD∥AC，
∴D（2，0），点D'与点D重合．
设直线FG的函数表达式为y＝qx+2，则﹣2q+2＝0，解得q＝1，
∴y＝x+2．
①如图2，点M1在点P左侧，PE、EM1为菱形的邻边．
连接PC，则CG＝PC，可得BC垂直平分PG，设垂足为点Q，
则点N1与点E关于点Q对称；
∵△PCE≌△BDE，
∴PE＝DE，E（3，3），
∵（2，4），
∴N1（1，5）；

②如图3，PE为菱形的对角线，M2N2垂直平分PE，设垂足为点R，
∵R为PE的中点，
∴R（，），
连接并延长BG交AC于点H，则△BGO≌△CAO，
∴∠GBO＝∠ACO，
∴∠GBO+∠CAO＝∠ACO+∠CAO＝90°，
∴BH⊥AC，
∴BH∥M2N2；
设直线BH的函数表达式为y＝rx+2，则6r+2＝0，解得r＝﹣，
∴y＝﹣x+2，
设直线M2N2的函数表达式为y＝﹣x+t，则﹣×+t＝，解得t＝，
∴y＝﹣x+；
由，得，
∴M2（，），
∵点N2与点M2（，）关于点R（，）对称，
∴N2（，）；

③如图4，点M3在点P右侧，PE、PM3为菱形的邻边．
由EN3∥FG，设直线的函数表达式为y＝x+s，则3+s＝3，解得s＝0，
∴点N3在直线y＝x上，
连接OE，则点O、E、N3在同一直线上．
设N3（d，d），
∵OE＝＝3，EN3＝PE＝＝，
∴d＝×（3+）＝3+，
∴N3（3+，3+）

④点M4在点P左侧，PE、PM4为菱形的邻边．
设N4（e，e），
则e＝×（3﹣）＝3﹣，
∴N4（3﹣，3﹣）．

综上所述，点N的坐标为（1，5）或（，）或（3+，3+）或（3﹣，3﹣）．
故答案为：（1，5）或（，）或（3+，3+）或（3﹣，3﹣）．
26．（8分）如图，已知△ABC中，∠ABC＝45°，CD是边AB上的高线，E是AC上一点，连接BE，交CD于点F．
（1）如图1，若∠ABE＝15°，BC＝+1，求DF的长；
（2）如图2，若BF＝AC，过点D作DG⊥BE于点G，求证：BE＝CE+2DG；
（3）如图3，若R为射线BA上的一个动点，以BR为斜边向外作等腰直角△BRH，M为RH的中点．在（2）的条件下，将△CEF绕点C旋转，得到△CE'F'，E，F的对应点分别为E'，F'，直线MF'与直线AB交于点P，tan∠ACD＝，直接写出当MF'取最小值时的值．

【分析】（1）如图1中，过点F作FH⊥BC于H．设FH＝CH＝m，则BH＝m，根据BC＝+1，构建方程求出m，即可解决问题．
（2）如图2中，连接DE，过点D作DH⊥DE交BE于H．证明BH＝EC，△DHE是等腰直角三角形即可解决问题．
（3）如图3中，过点M作MJ⊥BC于J，过点P作PK⊥BC于K．证明tan∠MBJ＝＝2，推出点M的在射线BM上运动，推出当C，F′，M共线，且CM⊥BM时，F′M的值最小．设AD＝m，想办法求出RM，PF′可得结论．
【解答】（1）解：如图1中，过点F作FH⊥BC于H．

∵CD⊥AB，
∴∠BDC＝90°，
∵∠DBC＝45°，
∴∠DCB＝90°﹣45°＝45°，
∵FH⊥CH，
∴∠FHC＝90°，
∴∠HFC＝∠HCF＝45°，
∴CH＝FH，
设FH＝CH＝m，
∵∠ABE＝15°，
∴∠FBC＝45°﹣15°＝30°，
∴BH＝HF＝m，
∴m+m＝+1，
∴m＝1，
∴CF＝CH＝，
∵CD＝BC＝，
∴DF＝CD﹣CF＝﹣＝．

（2）证明：如图2中，连接DE，过点D作DH⊥DE交BE于H．

∵∠ADC＝∠FDB＝90°，DB＝DC，BF＝AC，
∴Rt△BDF≌Rt△CDA（HL），
∴∠DBF＝∠ACD，
∵∠BFD＝∠CFE，
∴△BFD∽△CFE，
∴＝，
∴＝，
∵∠DFE＝∠BFC，
∴△DFE∽△BFC，
∴∠DEF＝∠BCF＝45°，
∵DH⊥DE，
∴∠HDE＝90°，
∴∠DHE＝∠DEH＝45°，
∴DH＝DE，
∵∠BDC＝∠EDH＝90°，
∴BDH＝∠CDE，
∵DB＝DC，DH＝DE，
∴△BDH≌△CDE（SAS），
∴BH＝EC，
∵DH＝DE，DG⊥EH，
∴GH＝EG，
∴DG＝EH，
∴BE＝BH+HE＝EC+2DG．

（3）解：如图3中，过点M作MJ⊥BC于J，过点P作PK⊥BC于K．

∵△BHR，△DBC都是等腰直角三角形，
∴∠DBC＝∠HBR＝45°，
∴∠HBC＝90°，
∵∠H＝∠HBJ＝∠MJB＝90°，
∴四边形BHMJ是矩形，
∴BH＝MJ，HM＝BJ，
∵BH＝HR，HM＝MR，
∴MJ＝2BJ，
∴tan∠MBJ＝＝2，
∴点M的在射线BM上运动，
∴当C，F′，M共线，且CM⊥BM时，F′M的值最小．
设AD＝m，
∵tan∠ACD＝＝，
∴CD＝BD＝3m，DF＝AD＝m，CF＝CF′＝2m，BC＝3m，
∵∠CMB＝90°，tan∠CBM＝＝2，
∴BM＝m，CM＝m，
∴BJ＝HM＝m，JM﹣BH＝HR＝m，
∴MR＝m，
设BK＝PK＝n，CK＝2n，
∴n＝m，
∴BK＝PK＝m，CK＝2m，PC＝m，
∴PF′＝PC﹣CF′＝m﹣2m，
∴＝＝．