中考冲刺-数学-第39课几何应用性问题

这是一份中考冲刺-数学-第39课几何应用性问题，共15页。PPT课件主要包含了考点跟踪训练等内容，欢迎下载使用。

　 　　第39课 几何应用性问题
要点梳理　几何应用题的形式有长度、面积、体积、角度以及三角函数的计算，还有方案设计等．基本解法：先根据题目已知条件准确画出图形，把生活情景的问题转化为数学问题，再运用几何计算中的一些基本方法予以解决．解题策略　　首先要阅读材料，理解题意，找到考查的主要内容和知识点，揭示实际问题的数学本质，把实际问题转化成数学问题．几何应用性问题的解题策略是：将实际问题几何化(从实际问题中抽象出基本几何图形)，解题时需要画出图形，在图形中标出已知线段长和角的度数等，注意几何与代数的联系，及数学思想方法的综合运用．用代数方法解几何应用题　　几何求值问题，当未知量不能直接求出时，一般需设出未知数，继而建立方程(组)，用解方程(组)的方法去求结果，这是解题中常见的具有导向作用的一种思想．
考点巩固测试 1.　小王购买了一套经济适用房，他准备将地面铺上地砖，地面结构如图所示．根据图中的数据(单位：m)，解答下列问题：　　(1)用含x、y的代数式表示地面总面积；　　(2)已知客厅面积比卫生间面积多21 m2，且地面总面积是卫生间面积的15倍．若铺1 m2地砖的平均费用为80元，那么铺地砖的总费用为多少元？ 解　(1)S＝6x＋3×2＋4×3＋2y＝6x＋2y＋18.∴总费用＝(6×4＋2×1.5＋18)×80＝3600(元)．感悟提高　　适当分割，将图形转化为便于求长度、面积的几何图形．
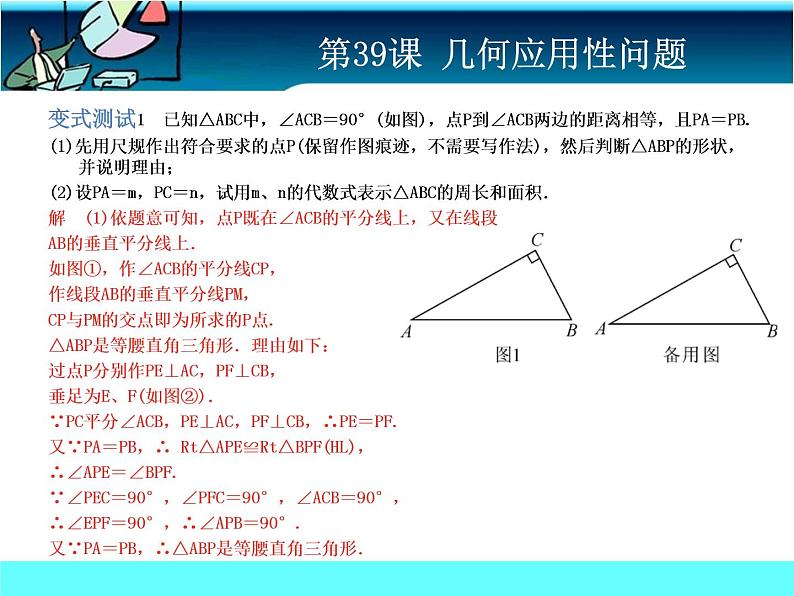
变式测试1　已知△ABC中，∠ACB＝90°(如图)，点P到∠ACB两边的距离相等，且PA＝PB.(1)先用尺规作出符合要求的点P(保留作图痕迹，不需要写作法)，然后判断△ABP的形状，并说明理由；(2)设PA＝m，PC＝n，试用m、n的代数式表示△ABC的周长和面积．解　(1)依题意可知，点P既在∠ACB的平分线上，又在线段AB的垂直平分线上．如图①，作∠ACB的平分线CP，作线段AB的垂直平分线PM，CP与PM的交点即为所求的P点. △ABP是等腰直角三角形．理由如下：过点P分别作PE⊥AC，PF⊥CB，垂足为E、F(如图②)．∵PC平分∠ACB，PE⊥AC，PF⊥CB，∴PE＝PF.又∵PA＝PB，∴ Rt△APE≌Rt△BPF(HL)，∴∠APE＝∠BPF.∵∠PEC＝90°，∠PFC＝90°，∠ACB＝90°，∴∠EPF＝90°，∴∠APB＝90°.又∵PA＝PB，∴△ABP是等腰直角三角形．
(2)如图②，在Rt△ABP中，∠APB＝90°，PA＝PB＝m，由Rt△APE≌Rt△BPF，△PCE≌△PCF可得，AE＝BF，CE＝CF，∴CA＋CB＝CE＋EA＋CB＝CE＋CF＝2CE.在Rt△PCE中，∠PEC＝90°，∠PCE＝45°，PC＝n，
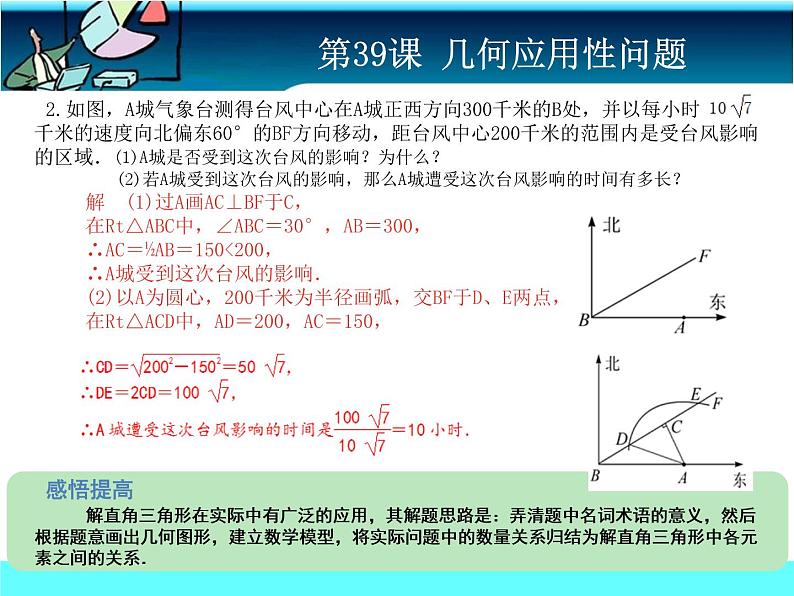
2.如图，A城气象台测得台风中心在A城正西方向300千米的B处，并以每小时 千米的速度向北偏东60°的BF方向移动，距台风中心200千米的范围内是受台风影响的区域．(1)A城是否受到这次台风的影响？为什么？　　 (2)若A城受到这次台风的影响，那么A城遭受这次台风影响的时间有多长？　　解　(1)过A画AC⊥BF于C，　　在Rt△ABC中，∠ABC＝30°，AB＝300，　　∴AC＝½AB＝150<200，　　∴A城受到这次台风的影响．　　(2)以A为圆心，200千米为半径画弧，交BF于D、E两点，　　在Rt△ACD中，AD＝200，AC＝150，　　 感悟提高　　解直角三角形在实际中有广泛的应用，其解题思路是：弄清题中名词术语的意义，然后根据题意画出几何图形，建立数学模型，将实际问题中的数量关系归结为解直角三角形中各元素之间的关系．
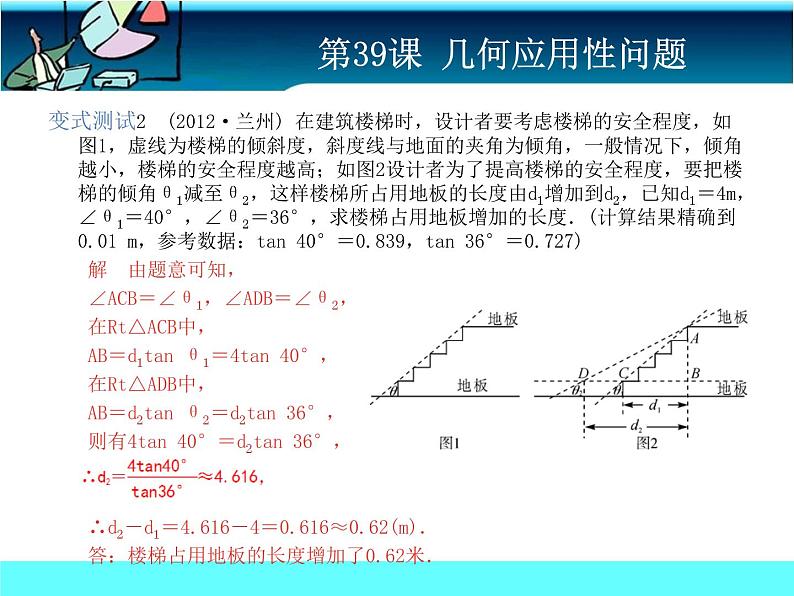
变式测试2　(2012·兰州) 在建筑楼梯时，设计者要考虑楼梯的安全程度，如图1，虚线为楼梯的倾斜度，斜度线与地面的夹角为倾角，一般情况下，倾角越小，楼梯的安全程度越高；如图2设计者为了提高楼梯的安全程度，要把楼梯的倾角θ1减至θ2，这样楼梯所占用地板的长度由d1增加到d2，已知d1＝4m，∠θ1＝40°，∠θ2＝36°，求楼梯占用地板增加的长度．(计算结果精确到0.01 m，参考数据：tan 40°＝0.839，tan 36°＝0.727)　　解　由题意可知，　　∠ACB＝∠θ1，∠ADB＝∠θ2，　　在Rt△ACB中，　　AB＝d1tan θ1＝4tan 40°，　　在Rt△ADB中，　　AB＝d2tan θ2＝d2tan 36°，　　则有4tan 40°＝d2tan 36°，　　　　∴d2－d1＝4.616－4＝0.616≈0.62(m)．　　答：楼梯占用地板的长度增加了0.62米．
3.　(2012·张家界) 黄岩岛是我国南海上的一个岛屿，其平面图如图甲所示，小明据此构造出该岛的一个数学模型，如图乙所示，其中∠B＝∠D＝90°，AB＝BC＝15千米，CD＝3 千米，请据此解答如下问题：　　(1)求该岛的周长和面积；(结果保留整数)　　(2)求∠ACD的余弦值． 解　(1)连接AC，∵AB＝BC＝15，∠B＝90°，∴∠BAC＝∠ACB＝45°，又∵∠D＝90°，
感悟提高　　当有些图形不是直角三角形时，可适当添加辅助线，把它们分割成直角三角形，把实际问题中的数量关系归结为直角三角形中各元素之间的关系．变式测试3　(2012·娄底) 如图，小红同学用仪器测量一棵大树AB的高度，在C处测得∠ADG＝30°，在E处测得∠AFG＝60°，CE＝8米，仪器高度CD＝1.5米，求这棵树AB的高度．(结果保留两位有效数字， ≈1.732) 　解　根据题意得：四边形DCEF和DCBG是矩形，　　∴GB＝EF＝CD＝1.5米，DF＝CE＝8米，　　设AG＝x米，GF＝y米，　　
　4.(2011·衢州) △ABC是一张等腰直角三角形纸板，∠C＝Rt∠，AC＝BC＝2.(1)要在这张纸板中剪出一个尽可能大的正方形，有甲、乙两种剪法(如图1)，比较甲、乙两种剪法，哪种剪法所得的正方形面积更大？请说明理由. 解　(1)如图甲，由题意得AE＝DE＝EC，即EC＝1，S正方形CFDE＝1.如图乙，设MN＝x，则由题意，得AM＝MQ＝PN＝NB＝MN＝x，说明：①图甲可另解，由题意得点D、E、F分别为AB、AC、BC的中点，S正方形CFDE＝S△ABC＝1；②本题亦可通过证EC＞MN来说明甲种剪法所得的正方形面积更大．
(2)图1中甲种剪法称为第1次剪取，记所得的正方形面积为S1；按照甲种剪法，在余下的△ADE和△BDF中，分别剪取正方形，得到两个相同的正方形，称为第2次剪取，并记这两个正方形面积和为S2(如图2)，则S2＝________；再在余下的四个三角形中，用同样的方法分别剪取正方形，得到四个相同的正方形，称为第3次剪取，并记这四个正方形的面积和为S3(如图3)；继续操作下去……，则第10次剪取时，S10＝________. 　(3)求第10次剪取后，余下的所有小三角形的面积和．　　
感悟提高 根据题意，画出符合题意的各种图形，再逐一用相应的几何知识解答．
变式测试4　在一服装厂里有大量形状为等腰三角形的边角布料(如图)．现找出其中的一种，测得∠C＝90°，AC＝BC＝4，现要从这种三角形中剪出一种扇形，做成不同形状的玩具，使扇形的边缘半径恰好都在△ABC的边上，且扇形与△ABC的其他边相切．请设计出所有可能符合题意的方案示意图，并求出扇形的半径(只要求画出图形，并直接写出扇形半径)．解