中考冲刺-数学-第40课探索性问题

这是一份中考冲刺-数学-第40课探索性问题，共22页。PPT课件主要包含了考点跟踪训练等内容，欢迎下载使用。

　 　　第40课　探索型问题
要点梳理　　　1. 规律探索型问题：是指数学对象所具备的状态或关系不明确，需对其本质属性进行探索，从而寻求、发现其所服从的某一特定规律或具有的不变性．规律探索问题的解题方法一般是利用特殊值(特殊点、特殊数量、特殊线段、特殊位置等)进行归纳、概括，从特殊到一般，从而得出结论．　　 2. 条件探索型问题：给出问题的结论，让解题者分析探索使结论成立应具备的条件，而满足结论的条件往往不唯一，需要采用证明、推断去探索发现并补充完善，使结论成立．它要求解题者善于从问题的结论出发，逆向追索，多途寻因．　　 3. 结论探索型问题：给定明确条件但未明确结论或结论不唯一，要求解题者充分利用条件进行大胆而合理的猜想，然后对猜想的结论进行证明．这类题主要考查解题者的发散思维和所学基本知识的应用能力．　　4. 存在探索型问题：指在一定条件下需探索发现某种数学关系是否存在的问题．解题时一般是先对结论作肯定存在的假设，然后由此肯定的假设出发，结合已知条件进行推理论证．若导出矛盾，则否定先前假设；若推出合理的结论，则说明假设正确，由此得出问题的结论．
四个解题方法　　(1)规律探索型问题：通过观察、类比特殊情况中数据特点，将数据进行分解重组、猜想、归纳得出规律，并用数学语言来表达这种规律，同时要用结论去检验特殊情况，以肯定结论的正确．　　(2)条件探索型问题：该类问题结论明确，需要完备条件，因此需要利用结论进行积极的探索，分析已知条件，要使结论成立还需什么条件，写出符合题意的条件．　　(3)结论探索型问题：该类问题仅给出某种情境而没有明确的结论，或结论不唯一，或结论需要类比、引伸推广，或题目给出特例，要通过归纳总结得出一般结论．探索时要将观察、猜想和结论有机地结合起来．　　(4)存在探索型问题：是指在某种条件下判断具有某种性质的数学结论是否存在的一类问题．解题时先假设结论成立，以此为条件进行运算或推理．若无矛盾，则假设成立，由此得出符合条件的结论成立；否则结论不存在．
对应巩固练习 1.　如图，在直角坐标系中，已知点P0的坐标为(1，0)，将线段OP0按逆时针方向旋转45°，再将其长度伸长为OP0的2倍，得到线段OP1；又将线段OP1按逆时针方向旋转45°，长度伸长为OP1的2倍，得到线段OP2；如此下去，得到线段OP3，OP4，…，OPn.(n为正整数) (1)求点P6的坐标； (2)求△P5OP6的面积；　 (3)我们规定：把点Pn(xn，yn)(n＝0，1，2，3，…)的横坐标xn、纵坐标yn都取绝对值后得到的新坐标(|xn|，|yn|)称之为点Pn的“绝对坐标”． 根据图中点Pn的分布规律，请你猜想点Pn的“绝对坐标”， 并写出来．
(3)点Pn的坐标可分三类情况：①当n＝8k或n＝8k＋4时(其中k为自然数)，点Pn落在x轴上，此时，点Pn的绝对坐标为(2n，0)；②当n＝8k＋1或8k＋3或8k＋5或8k＋7时(其中k为自然数)，点Pn落在各象限的平分线上，此时，点Pn的绝对坐标为③当n＝8k＋2或8k＋6时(其中k为自然数)，点Pn落在y轴上，此时，点Pn的绝对坐标为(0，2n)． 感悟提高　　本题属于规律探索型问题，数学对象所具备的状态或关系不明确时，需对其本质属性进行探索，从而寻求、发现其所服从的某一特定规律或具有的不变性．解题方法一般是利用特殊值(特殊点、特殊数量、特殊线段、特殊位置等)进行归纳、概括，从特殊到一般，从而得出规律．
变式测试1　已知下列n(n为正整数)个关于x的一元二次方程：①x2－1＝0；②x2＋x－2＝0；③x2＋2x－3＝0；…；（n）x2＋(n－1)x－n＝0.　(1)请解上述一元二次方程①、②、③、…(n)；　(2)请你指出这n个方程的根具有什么共同特点，写出一条即可．解　(1)方程①:x2－1＝0的解是x1＝1，x2＝－1；方程②:x2＋x－2＝0的解是x1＝1，x2＝－2；方程③:x2＋2x－3＝0的解是x1＝1，x2＝－3；…；方程(n):x2＋(n－1)x－n＝0的解是x1＝1，x2＝－n.(2)这n个方程都有一个根是x＝1.
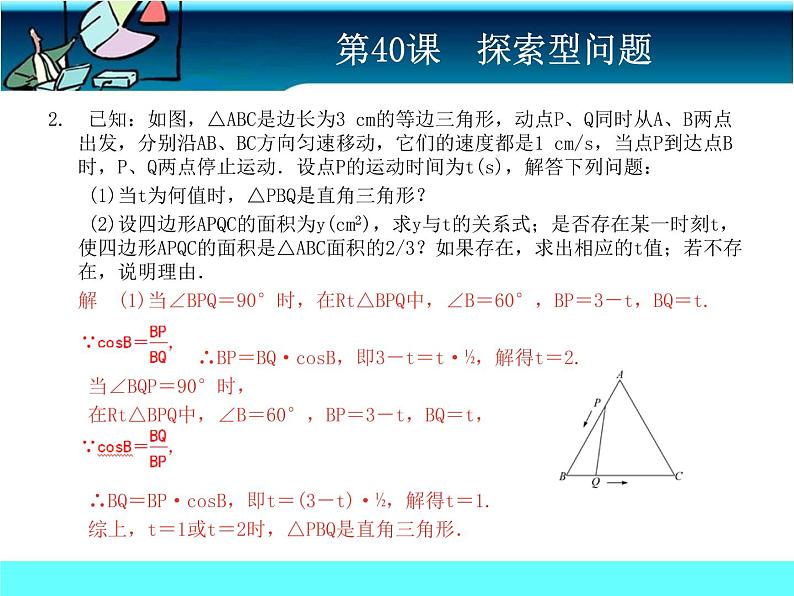
2.　已知：如图，△ABC是边长为3 cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1 cm/s，当点P到达点B时，P、Q两点停止运动．设点P的运动时间为t(s)，解答下列问题： (1)当t为何值时，△PBQ是直角三角形？ (2)设四边形APQC的面积为y(cm2)，求y与t的关系式；是否存在某一时刻t，使四边形APQC的面积是△ABC面积的2/3？如果存在，求出相应的t值；若不存在，说明理由． 解　(1)当∠BPQ＝90°时，在Rt△BPQ中，∠B＝60°，BP＝3－t，BQ＝t.　　 ∴BP＝BQ·csB，即3－t＝t·½，解得t＝2.　　当∠BQP＝90°时，　　在Rt△BPQ中，∠B＝60°，BP＝3－t，BQ＝t，　　　∴BQ＝BP·csB，即t＝(3－t)·½，解得t＝1.　　综上，t＝1或t＝2时，△PBQ是直角三角形．
感悟提高　　存在探索题是指在一定条件下，需探索发现某种数学关系是否存在的问题．解题方法一般是先对结论作肯定存在的假设，然后由此肯定的假设出发，结合已知条件进行推理论证，若导出矛盾，则否定先前假设；若推出合理的结论，则说明假设正确
变式测试2　(2011·常德) 如图，已知抛物线过点A(0，6)，B(2，0)，C(7， )．　(1)求抛物线的解析式；　(2)若D是抛物线的顶点，E是抛物线的对称轴与直线AC的交点，F与E关于D对称，求证：∠CFE＝∠AFE；　(3)在y轴上是否存在这样的点P，使△AFP与△FDC相似？ 若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．解　(1)设经过点A(0，6)，B(2，0)，C(7， )的抛物线的解析式为y＝ax2＋bx＋c，∴此抛物线的解析式为 y＝x2－4x＋6.

3.　已知：如图①，在Rt△ACB中，∠C＝90°，AC＝4 cm，BC＝3 cm，点P由B出发沿BA方向向点A匀速运动，速度为1 cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2 cm/s；连接PQ.若设运动的时间为t(s)(0感悟提高 本题结论明确，因此需探索发现使结论成立的条件．
变式测试3　如图，四边形OABC是一张放在平面直角坐标系中的矩形纸片，点A在x轴上，点C在y轴上，将边BC折叠，使点B落在边OA上的点D处．已知折痕CE＝ 且tan∠EDA＝¾.　(1)判断△OCD与△ADE是否相似？请说明理由；　(2)求直线CE与x轴交点P的坐标；　(3)是否存在过点D的直线l，使直线l、直线CE与x轴所围成的三角形和直线l、直线CE与y轴所围成的三角形相似？如果存在，请直接写出其解析式并画出相应的直线；如果不存在，请说明理由． 　　解　(1)△OCD∽△ADE.　　理由如下：　　由折叠知：∠CDE＝∠B＝90°，　　∴∠1＋∠2＝90°，　　∵∠1＋∠3＝90°，　　∴∠2＝∠3.　　又∵∠COD＝∠DAE＝90°， 　　∴△OCD∽△ADE.
(3)满足条件的直线l有2条：y＝－2x＋12，y＝2x－12.如图中的l1、l2.