初中数学人教版八年级下册第十八章 平行四边形综合与测试单元测试当堂达标检测题

人教版数学八年级下册

《平行四边形》单元测试题

一、选择题

1.如图，四边形ABCD的对角线交于点O，下列哪组条件不能判断四边形ABCD是平行四边形(     )

A.OA=OC，OB=OD

B.∠BAD=∠BCD，AB∥CD

C.AD∥BC，AD=BC

D.AB=CD，AO=CO

2.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是(　　)

A.当AB=BC时,它是菱形

B.当AC⊥BD时,它是菱形

C.当∠ABC=90°时,它是矩形

D.当AC=BD时,它是正方形

3.在数学活动课上，老师和同学们判断一个四边形门框是否为矩形，下面是某合作学习小组的4位同学拟定的方案，其中正确的是(    )

A.测量对角线是否相互平分

B.测量两组对边是否分别相等

C.测量一组对角是否为直角

D.测量四边形的其中三个角是否都为直角

4.如图，平行四边形ABCD的对角形AC，BD相交于点O，下列结论正确的是(     )

A.S▱ABCD=4S△AOB

B.AC=BD

C.AC⊥BD

D.平行四边形ABCD是轴对称图形

5.如图，在矩形ABCD中，E为CD的中点，连接AE并延长交BC的延长线于点F，则图中全等的直角三角形共有（  ）

A.6对                                   B.5对                         C.4对                                      D.3对

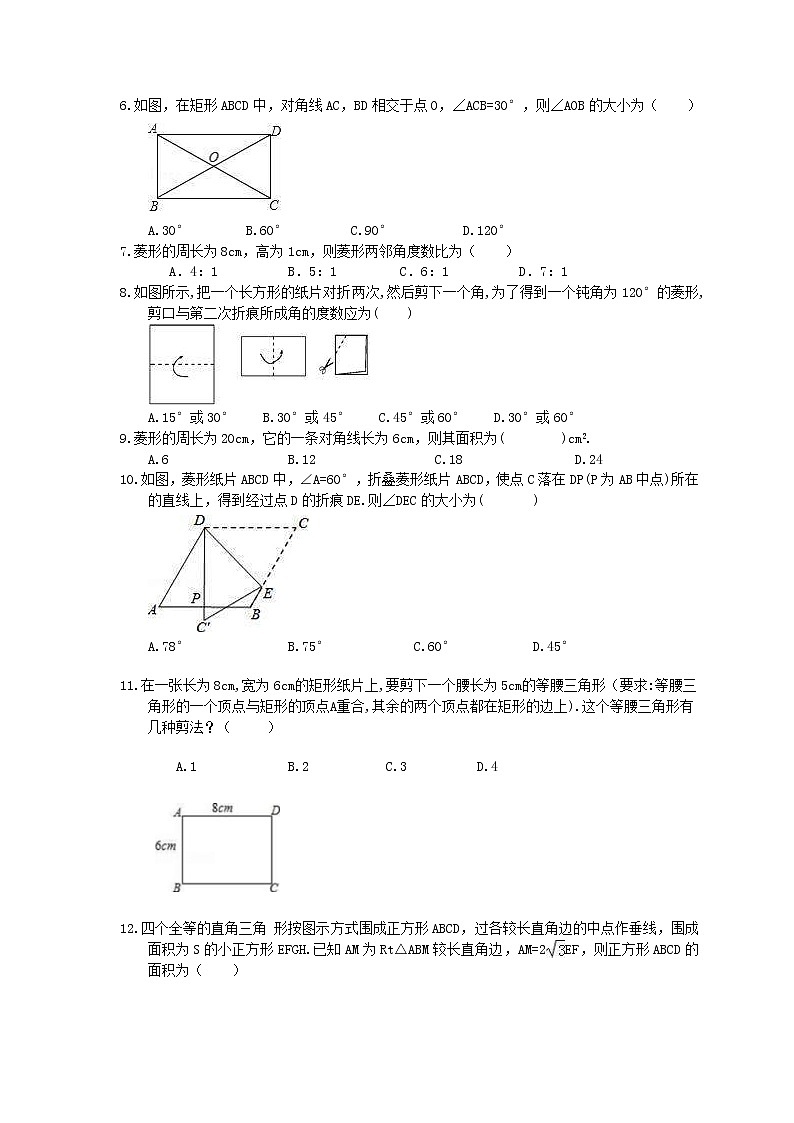
6.如图，在矩形ABCD中，对角线AC，BD相交于点O，∠ACB=30°，则∠AOB的大小为（　　）

A.30°                      B.60°                       C.90°                        D.120°

7.菱形的周长为8cm，高为1cm，则菱形两邻角度数比为（    ）

   A．4：1                        B．5：1                       C．6：1                        D．7：1

8.如图所示,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为120°的菱形,剪口与第二次折痕所成角的度数应为(　　)

A.15°或30°　　B.30°或45°　　C.45°或60°　　D.30°或60°

9.菱形的周长为20cm，它的一条对角线长为6cm，则其面积为(　    　)cm2.

A.6           B.12             C.18            D.24

10.如图，菱形纸片ABCD中，∠A=60°，折叠菱形纸片ABCD，使点C落在DP(P为AB中点)所在的直线上，得到经过点D的折痕DE.则∠DEC的大小为(　   　)

A.78°            B.75°         C.60°         D.45°

11.在一张长为8cm,宽为6cm的矩形纸片上,要剪下一个腰长为5cm的等腰三角形（要求:等腰三角形的一个顶点与矩形的顶点A重合,其余的两个顶点都在矩形的边上).这个等腰三角形有几种剪法？（     ）

    A.1             B.2           C.3          D.4

12.四个全等的直角三角 形按图示方式围成正方形ABCD，过各较长直角边的中点作垂线，围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边，AM=2EF，则正方形ABCD的面积为（　　）

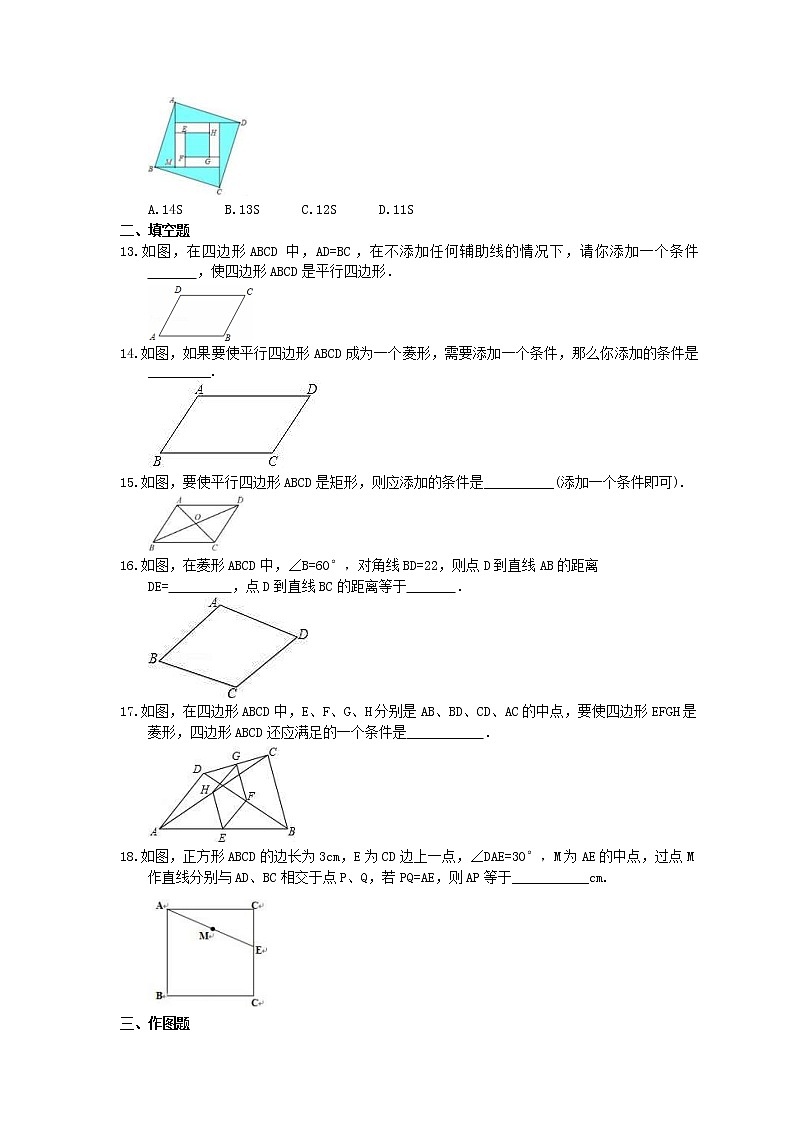
A.14S      B.13S      C.12S      D.11S

二、填空题

13.如图，在四边形ABCD中，AD=BC，在不添加任何辅助线的情况下，请你添加一个条件　   　，使四边形ABCD是平行四边形．

14.如图，如果要使平行四边形ABCD成为一个菱形，需要添加一个条件，那么你添加的条件是_________.

15.如图，要使平行四边形ABCD是矩形，则应添加的条件是__________(添加一个条件即可).

16.如图，在菱形ABCD中，∠B=60°，对角线BD=22，则点D到直线AB的距离DE=　　     ，点D到直线BC的距离等于　　   ．

17.如图，在四边形ABCD中，E、F、G、H分别是AB、BD、CD、AC的中点，要使四边形EFGH是菱形，四边形ABCD还应满足的一个条件是　       　．

18.如图，正方形ABCD的边长为3cm，E为CD边上一点，∠DAE=30°，M为AE的中点，过点M作直线分别与AD、BC相交于点P、Q，若PQ=AE，则AP等于___________cm.

三、作图题

19.如图，在8×8的正方形网格中，△ABC的顶点在边长为1的小正方形的顶点上.

（1）填空：∠ABC=　  　，BC=　    ；

（2）若点A在网格所在的坐标平面里的坐标为（﹣2，0），请你在图中找出一点D，使以A、B、C、D四个点为顶点的平行四边形，满足条件的D点的坐标可以是　    　（写出一个即可）.

四、解答题

20.如图，已知在▱ABCD中，延长DA到点E，延长BC到点F，使得AE=CF，连接EF，分别交AB，CD于点M，N，连接DM，BN.

（1）求证：△AEM≌△CFN；

（2）求证：四边形BMDN是平行四边形.

21.如图，在四边形ABCD中，BD为一条对角线，AD∥BC，AD=2BC，∠ABD=90°，E为AD的中点，连接BE.

（1）求证：四边形BCDE为菱形；

（2）连接AC，若AC平分∠BAD，判断AC与CD的数量关系和位置关系，并说明理由.

(1)证明:四边形ACDE是平行四边形;

(2)若AC=8,BD=6,求△ADE的周长.

23.如图，E，F分别是正方形ABCD的边CB，DC延长线上的点，且BE=CF，过点E作EG∥BF，交正方形外角的平分线CG于点G，连接GF．求证：

(1)AE⊥BF；

(2)四边形BEGF是平行四边形．

24.如图，点E、F为线段BD的两个三等分点，四边形AECF是菱形．

（1）试判断四边形ABCD的形状，并加以证明；

（2）若菱形AECF的周长为20，BD为24，试求四边形ABCD的面积．

五、综合题

25.如图，正方形ABCD中，G为射线BC上一点，连接AG，过G点作GN⊥AG，再作∠DCM的平分线，交GN于点H.

（1）如图1，当G是线段BC的中点时，求证：AG=GH；

（2）如图2，当G是线段BC上任意一点时，（1）中结论还成立吗？若不成立请说明理由；若成立，请写出证明过程.

（3）当G是线段BC的延长线上任意一点时，（1）中结论还成立吗？若不成立请说明理由；若成立，请写出证明过程.

0.参考答案

1.答案为：D

2.D

3.答案为：D

4.答案为：A

5.C

6.B

7.B.

9.答案为：D.

10.B

11.C

12.答案为：B.

解：设AM=2a.BM=b.则正方形ABCD的面积=4a2+b2

由题意可知EF=（2a﹣b）﹣2（a﹣b）=2a﹣b﹣2a+2b=b，

∵AM=2EF，∴2a=2b，∴a=b，

∵正方形EFGH的面积为S，∴b2=S，

∴正方形ABCD的面积=4a2+b2=13b2=13S，故选B.

13.答案为：AD∥BC(答案不唯一)

14.答案为：AB=AD或AC⊥BD；

15.答案为：不唯一，如：∠ABC=90°或AC=BD

16.答案为：11，11．

17.答案为：AD=BC;

18.答案为：1或2；

19.解：（1）∠ABC=90°+45°=135°，BC==2；故答案为：135°，2；

（2）∵A的坐标为（﹣2，0），∴坐标系如图所示：

当CD∥AB，CD=AB=2时，四边形ABCD是平行四边形，点D的坐标为（0，﹣2）；

故答案为：（0，﹣2）（答案不唯一）.

20.证明：（1）四边形ABCD是平行四边形，

∴∠DAB=∠BCD，∴∠EAM=∠FCN，

又∵AD∥BC，∴∠E=∠F.

∵在△AEM与△CFN中，

，

∴△AEM≌△CFN（ASA）；

（2）∵四边形ABCD是平行四边形，∴ABCD，

又由（1）得AM=CN，∴BMDN，

∴四边形BMDN是平行四边形.

21.

∴AB∥CD,AC⊥BD,

∴AE∥CD,∠AOB=90°,

又∵DE⊥BD,即∠EDB=90°,

∴∠AOB=∠EDB.

∴DE∥AC.

∴四边形ACDE是平行四边形.

(2)∵四边形ABCD是菱形,AC=8,BD=6,

∴AO=4,DO=3,

∴AD=CD=5.

又∵四边形ACDE是平行四边形,

∴AE=CD=5,DE=AC=8.

∴△ADE的周长为AD+AE+DE=5+5+8=18.

23.证明：

(1)∵四边形ABCD是正方形，∴AB=BC，∠ABC=∠BCD=90°，

∴∠ABE=∠BCF=90°，

在△ABE和△BCF中，，∴△ABE≌△BCF(SAS)，

∴AE=BF，∠BAE=∠CBF，

∵EG∥BF，∴∠CBF=∠CEG，

∵∠BAE+∠BEA=90°，∴∠CEG+∠BEA=90°，

∴AE⊥EG，

∴AE⊥BF；

(2)延长AB至点P，使BP=BE，连接EP，如图所示：则AP=CE，∠EBP=90°，

∴∠P=45°，

∵CG为正方形ABCD外角的平分线，∴∠ECG=45°，∴∠P=∠ECG，

由(1)得∠BAE=∠CEG，

在△APE和△ECG中，，∴△APE≌△ECG(ASA)，∴AE=EG，

∵AE=BF，∴EG=BF，

∵EG∥BF，

∴四边形BEGF是平行四边形．

（1）四边形ABCD为菱形．

理由如下：如图，连接AC交BD于点O，

∵四边形AECF是菱形，

∴AC⊥BD，AO=OC，EO=OF，

又∵点E、F为线段BD的两个三等分点，

∴BE=FD，

∴BO=OD，

∵AO=OC，

∴四边形ABCD为平行四边形，

∵AC⊥BD，

∴四边形ABCD为菱形；

（2）∵四边形AECF为菱形，且周长为20，

∴AE=5，

∵BD=24，

∴EF=8，OE=EF=×8=4，

由勾股定理得，AO===3，

∴AC=2AO=2×3=6，

∴S四边形ABCD=BD•AC=×24×6=72．

25.（1）证明：如图1，取AB的中点E，连接GE，则GC=AE.

∵四边形ABCD是正方形，G是线段BC的中点，

∴BG=BE=AE=GC，

∴△BEG为等腰直角三角形，∴∠AEG=135°，

而CH是∠DCM的平分线，∴∠GCH=135°，∴∠AEG=∠GCH.

∵AG⊥GH，∴∠CGH+∠AGB=90°，

又∵∠EAG+∠AGB=90°，∴∠EAG=∠CGH.

在△AEG与△GCH中，，∴△AEG≌△GCH（ASA），

∴AG=GH；

（2）解：当G是线段BC上任意一点时，AG=GH仍成立.理由如下：

如图2，在AB上取一点E，使AE=GC，连接EG.

∵四边形ABCD是正方形，CH平分∠DCM，∴∠GCH=135°.

∵BE=BG，∴∠BEG=45°，∴∠AEG=135°，∴∠AEG=∠GCH.

∵AG⊥GH，∴∠CGH+∠AGB=90°，

又∵∠EAG+∠AGB=90°，∴∠EAG=∠CGH.

在△AEG与△GCH中，，∴△AEG≌△GCH（ASA），

∴AG=GH；

（3）解：当G是线段BC的延长线上任意一点时，AG=GH仍成立.理由如下：

如图3，在BA的延长线上取一点E，使AE=GC，连接EG，则BE=BG.

∵∠B=90°，BG=BE，∴∠AEG=45°，

又∠GCH=45°，∴∠AEG=∠GCH.

∵∠EAG=90°+∠DAG，∠CGH=90°+∠BGA，

∵AD∥CB，∴∠DAG=∠BGA，∴∠EAG=∠CGH.

在△AEG与△GCH中，，∴△AEG≌△GCH（ASA），

∴AG=GH.