2020-2021学年湖北省武汉市硚口区八年级（下）期中数学试卷 Word版

这是一份2020-2021学年湖北省武汉市硚口区八年级（下）期中数学试卷 Word版，共6页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。

1．在二次根式中，m的取值范围是（ ）
A．m≥2B．m＞2C．m≠2D．m≥﹣2
2．下列各式计算正确的是（ ）
A．×＝6B．÷＝2C．（）2＝9D．（3）2＝6
3．在三边分别为下列长度的三角形中，不是直角三角形的是（ ）
A．6，8，10B．1，，C．2，3，D．4，5，7
4．在▱ABCD中，如果∠A+∠C＝140°，那么∠C的大小是（ ）
A．20°B．40°C．70°D．75°
5．如图，在正方形OABC中，O是坐标原点，点A的坐标为（1，），则点C的坐标是（ ）
A．（﹣，1）B．（﹣1，）C．（，1）D．（﹣，﹣1）
6．下列四个命题：
①若三角形三边的比为1：1：2，则它是等腰直角三角形；
②对角线相等的平行四边形是矩形；
③对角线互相平分且相等的四边形是矩形；
④两个邻角相等的平行四边形是矩形．
其中真命题的个数是（ ）
A．1B．2C．3D．4
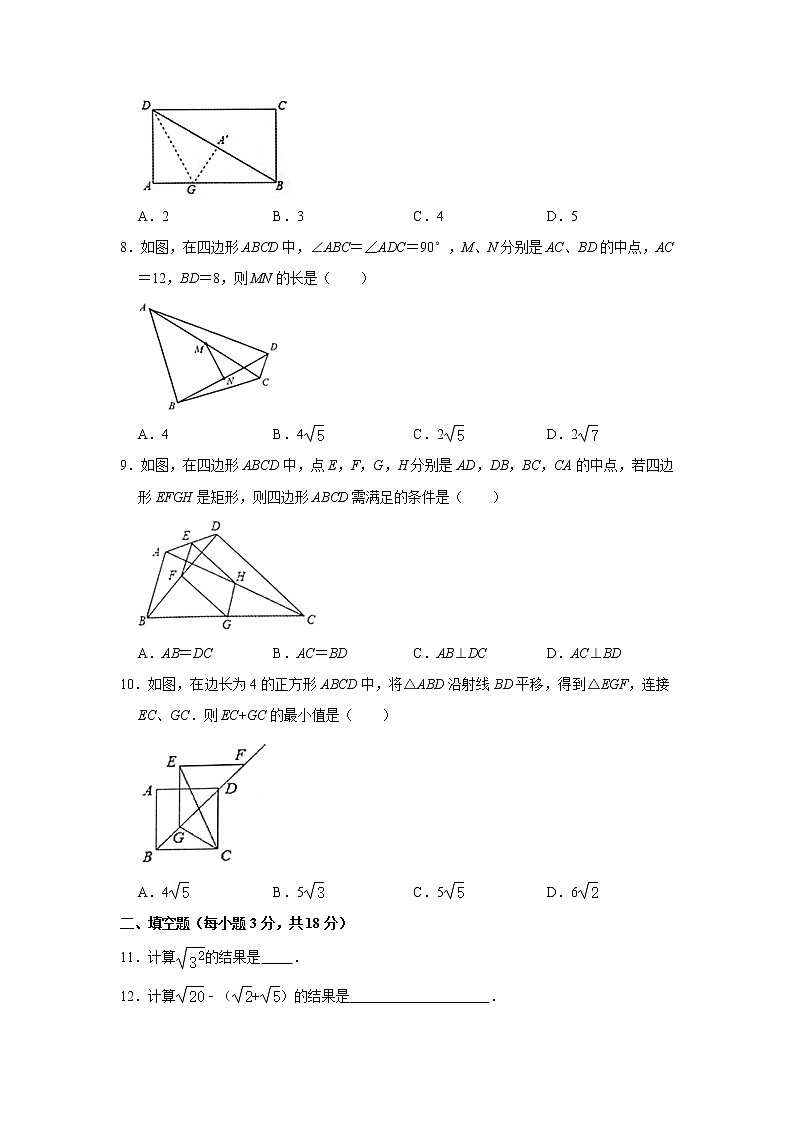
7．如图，在矩形纸片ABCD中，AB＝8，AD＝6，折叠纸片使边AD落在对角线BD上，折痕为DG，则AG的长是（ ）
A．2B．3C．4D．5
8．如图，在四边形ABCD中，∠ABC＝∠ADC＝90°，M、N分别是AC、BD的中点，AC＝12，BD＝8，则MN的长是（ ）
A．4B．4C．2D．2
9．如图，在四边形ABCD中，点E，F，G，H分别是AD，DB，BC，CA的中点，若四边形EFGH是矩形，则四边形ABCD需满足的条件是（ ）
A．AB＝DCB．AC＝BDC．AB⊥DCD．AC⊥BD
10．如图，在边长为4的正方形ABCD中，将△ABD沿射线BD平移，得到△EGF，连接EC、GC．则EC+GC的最小值是（ ）
A．4B．5C．5D．6
二、填空题（每小题3分，共18分）
11．计算的结果是 ．
12．计算﹣（+）的结果是 ．
13．如图，网格中每个小正方形的边长均为1，以A为圆心，AB为半径画弧，交最上方的网格线于点D，则ED的长是 ．
14．在正方形ABCD中，点E在直线BC上，CE＝AD，连接AE，则∠EAD的大小是 ．
15．如图，将四边形纸片ABCD沿过点A的直线折叠，使得点B落在CD上的点Q处．折痕为AP；再将△PCQ，△ADQ分别沿PQ，AQ折叠，此时点C，D落在AP上的同一点R处．当四边形APCD是平行四边形时，的值是 ．
16．如图，点P是正方形ABCD内一点，PA＝2，PB＝，∠APB＝135°，则PC的长是 ．
三、解答题（共8小题，共72分）
17．计算：
（1）+﹣（﹣）；
（2）+8﹣x．
18．如图，矩形ABCD是一个底部直径BC为12cm的杯子的示意图，在它的正中间竖直放一根筷子EG，筷子漏出杯子外2cm，当筷子倒向杯壁时（筷子底端E不动），筷子顶端正好触到杯口，求筷子EG的长度．
19．如图，在四边形ABCD中，∠B＝90°，AB＝BC＝2，AD＝1，CD＝3．
（1）求∠DAB的度数；
（2）求四边形ABCD的面积．
20．如图，菱形ABCD的对角线AC，BD相交于点O，E是AD的中点，点F，G在AB上，EF⊥AB，OG∥EF．
（1）求证：四边形OEFG是矩形；
（2）若AD＝10，EF＝4，求OE和BG的长．
21．如图，在▱ABCD中，点E，F在对角线AC上，DE∥BF，连接BE，DF．
（1）求证：△ADE≌△CBF；
（2）若BE＝DE，求证：四边形ABCD是菱形．
22．由边长为1的小正方形构成网格，每个小正方形的顶点叫做格点，点A、B、C都是格点，点P是AB与网格线的交点．仅用无刻度的直尺在给定9X12的网格中完成画图，画图过程用虚线表示，画图结果用实线表示，并回答下列问题：
（1）直接写出AB的长是 ；
（2）在图1中，画以点A、B、C为顶点且周长最大的平行四边形；
（3）在图1中，画△ABC的角平分线AD；
（4）在图2中，过点P画线段PQ，使PQ⊥AB，且PQ＝AB．
23．如图1，在矩形ABCD中，点E在BA的延长线上，AE＝AD，EC与BD相交于点G，与AD相交于点F，AF＝AB．
（1）求证：BD⊥EC；
（2）求证：+＝；
（3）如图2，连接AG，求证：EG﹣DG＝AG．
24．在正方形ABCD中，点E是边BC上一动点（不含端点B、C）．
（1）如图1，AE⊥EP，AE＝EF，连接CF．
①求∠ECF的大小；
②如图2，N为CF的中点，连接DN、DE，求证：DE＝DN；
（2）如图3．若AD＝1+，直接写出BE+DE的最小值．