2020-2021学年广东省深圳市七年级(下)期中数学试卷
展开1.下列运算正确的是( )
A.a3+a3=a6B.(3ab)2=6ab2
C.a6÷a2=a3D.(﹣a3)2=a6
2.华为麒麟990芯片采用了最新的0.000000007米的工艺制程,数0.000000007用科学记数法表示为( )
A.7×10﹣9B.7×10﹣8C.0.7×10﹣9D.0.7×10﹣8
3.在下列多项式的乘法中,可以用平方差公式计算的是( )
A.(2x+y)(2y﹣x)B.(x+1)(﹣x﹣1)
C.(3x﹣y)(3x+y)D.(x﹣y)(﹣x+y)
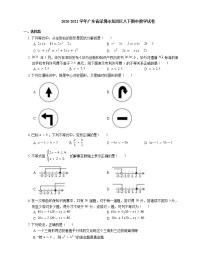
4.如图所示,过点P画直线a的平行线b的作法的依据是( )
A.两直线平行,同位角相等
B.同位角相等,两直线平行
C.两直线平行,内错角相等
D.内错角相等,两直线平行
5.如图,在长方形ABCD中,AB=2,BC=1.动点P从点B出发,沿路线B﹣C﹣D作匀速运动,那么△ABP的面积S与点P的运动路程x之间关系的图象大致是( )
A.B.
C.D.
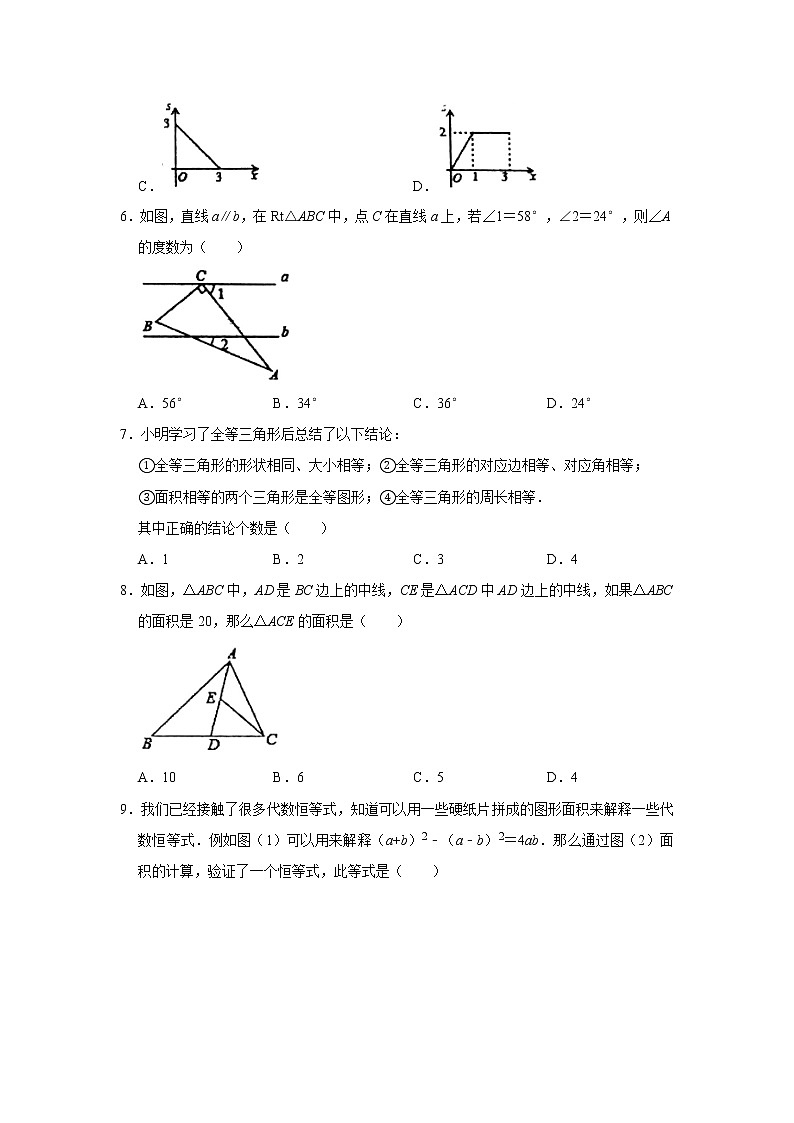
6.如图,直线a∥b,在Rt△ABC中,点C在直线a上,若∠1=58°,∠2=24°,则∠A的度数为( )
A.56°B.34°C.36°D.24°
7.小明学习了全等三角形后总结了以下结论:
①全等三角形的形状相同、大小相等;②全等三角形的对应边相等、对应角相等;
③面积相等的两个三角形是全等图形;④全等三角形的周长相等.
其中正确的结论个数是( )
A.1B.2C.3D.4
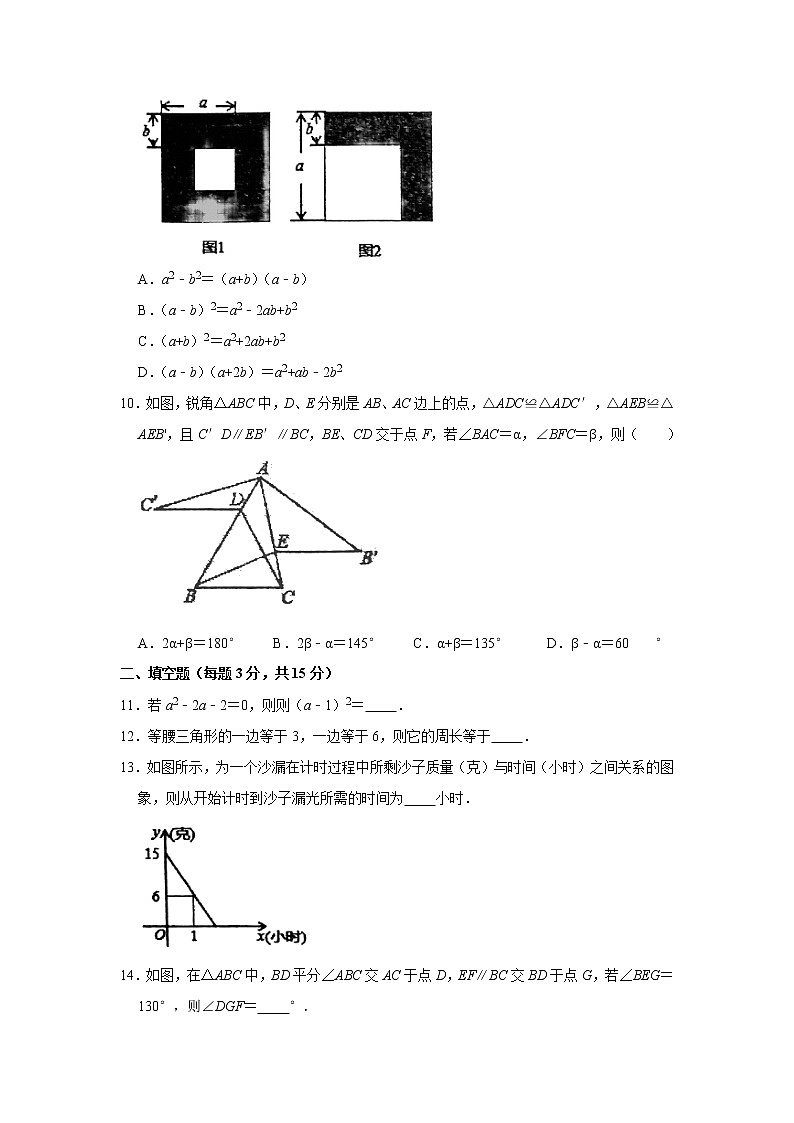
8.如图,△ABC中,AD是BC边上的中线,CE是△ACD中AD边上的中线,如果△ABC的面积是20,那么△ACE的面积是( )
A.10B.6C.5D.4
9.我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图(1)可以用来解释(a+b)2﹣(a﹣b)2=4ab.那么通过图(2)面积的计算,验证了一个恒等式,此等式是( )
A.a2﹣b2=(a+b)(a﹣b)
B.(a﹣b)2=a2﹣2ab+b2
C.(a+b)2=a2+2ab+b2
D.(a﹣b)(a+2b)=a2+ab﹣2b2
10.如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB',且C′D∥EB′∥BC,BE、CD交于点F,若∠BAC=α,∠BFC=β,则( )
A.2α+β=180°B.2β﹣α=145°C.α+β=135°D.β﹣α=60°
二、填空题(每题3分,共15分)
11.若a2﹣2a﹣2=0,则则(a﹣1)2= .
12.等腰三角形的一边等于3,一边等于6,则它的周长等于 .
13.如图所示,为一个沙漏在计时过程中所剩沙子质量(克)与时间(小时)之间关系的图象,则从开始计时到沙子漏光所需的时间为 小时.
14.如图,在△ABC中,BD平分∠ABC交AC于点D,EF∥BC交BD于点G,若∠BEG=130°,则∠DGF= °.
15.如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为AB,CD.若CD∥BE,∠1=28°,则∠2的度数是 .
三、解答题(共7小题,共55分)
16.(1)计算:2x(x﹣3y)+(5xy2﹣2x2y)÷y;
(2)计算:(2x﹣3y﹣1)(2x+3y﹣1);
(3)先化简,再求值:[(x+2y)2﹣(3x+y)(﹣y+3x)﹣5y2]÷(﹣x),其中(2x+1)2+|y﹣2|=0.
17.(1)已知m+n=4,mn=2,求m2+n2的值;
(2)已知am=3,an=5,求a3m﹣2n的值.
18.在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下表是测得的弹簧的长度y与所挂物体的质量x的几组对应值.
(1)本题反映的是弹簧的长度y与所挂物体的质量x这两个变量之间的关系,其中自变量是 ,因变量是 .
(2)当所悬挂重物为3kg时,弹簧的长度为 cm;不挂重物时,弹簧的长度为 cm.
(3)请直接写出弹簧长度y(cm)与所挂物体质量x(kg)的关系式,并计算若弹簧的长度为36cm时,所挂重物的质量是多少kg?(在弹簧的允许范围内)
19.如图,在△ABC中AD、AE、AF分别为△ABC的高、角平分线和中线,已知△AFC的面积为10,AD=4,∠DAE=20°,∠C=30°.
(1)求BC的长度.
(2)求∠B的度数.
20.若x满足(9﹣x)(x﹣4)=4,求(9﹣x)2+(x﹣4)2的值.
解:设9﹣x=a,x﹣4=b,则(9﹣x)(x﹣4)=ab=4,a+b=(9﹣x)+(x﹣4)=5,
∴(9﹣x)2+(x﹣4)2=a2+b2=(a+b)2﹣2ab=52﹣2×4=17
请仿照上面的方法求解下面问题:
(1)若x满足(5﹣x)(x﹣2)=2,求(5﹣x)2+(x﹣2)2的值;
(2)如图,在长方形ABCD中,AB=20,BC=12,点E.F是BC、CD上的点,且BE=DF=x,分别以FC、CE为边在长方形ABCD外侧作正方形CFGH和CEMN,若长方形CEPF的面积为160平方单位,则图中阴影部分的面积和为多少平方单位?
21.如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F.
(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为 ;
(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数是多少?
22.如图所示,已知射线CB∥OA,∠C=∠OAB=120°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之变化?若变化,请找出规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC﹣∠OBA=10°?若存在,求出∠BOA度数;若不存在,请说明理由.
所挂物体质量x/kg
0
1
2
3
4
5
弹簧长度y/cm
18
20
22
24
26
28
2020-2021学年广东省深圳市南山区南海中学七年级(下)期中数学试卷(含解析): 这是一份2020-2021学年广东省深圳市南山区南海中学七年级(下)期中数学试卷(含解析),共21页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2020-2021学年广东省深圳市龙岗区八下期中数学试卷: 这是一份2020-2021学年广东省深圳市龙岗区八下期中数学试卷,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2020-2021学年广东省深圳市宝安区八下期中数学试卷(图片版): 这是一份2020-2021学年广东省深圳市宝安区八下期中数学试卷(图片版),共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。