初中数学人教版八年级下册第十八章 平行四边形综合与测试练习题

这是一份初中数学人教版八年级下册第十八章 平行四边形综合与测试练习题，共20页。试卷主要包含了下列说法中正确的是等内容，欢迎下载使用。

一．选择题（共10小题，满分30分，每小题3分）
1．在▱ABCD中，已知∠A﹣∠B＝20°，则∠C＝（ ）
A．60°B．80°C．100°D．120°
2．下列说法中正确的是（ ）
A．有一个角是直角的四边形是矩形
B．两条对角线互相垂直的四边形是菱形
C．两条对角线互相垂直平分的四边形是正方形
D．两条对角线相等的菱形是正方形
3．如图，为测量位于一水塘旁的两点A，B间的距离，在地面上确定点O，分别取OA，OB的中点C，D，量得CD＝10m，则A，B之间的距离是（ ）
A．5mB．10mC．20mD．40m
4．不能判定四边形ABCD是平行四边形的条件是（ ）
A．AB＝CD，AD＝BCB．AB∥CD，∠B＝∠D
C．∠A＝∠B，∠C＝∠DD．AB＝CD，∠BAC＝∠ACD
5．已知▱ABCD的周长为24，AB＝4，则BC的长为（ ）
A．6B．8C．10D．12
6．若菱形的两条对角线长分别是6和8，则它的周长为（ ）
A．20B．24C．40D．48
7．如图，矩形ABCD的两条对角线相交于点O，∠AOD＝60°，AD＝1，则AB的长是（ ）
A．1B．2C．D．2
8．如图，菱形ABCD的周长为52，对角线AC的长为24，DE⊥AB，垂足为E，则DE的长为（ ）
A．B．C．D．
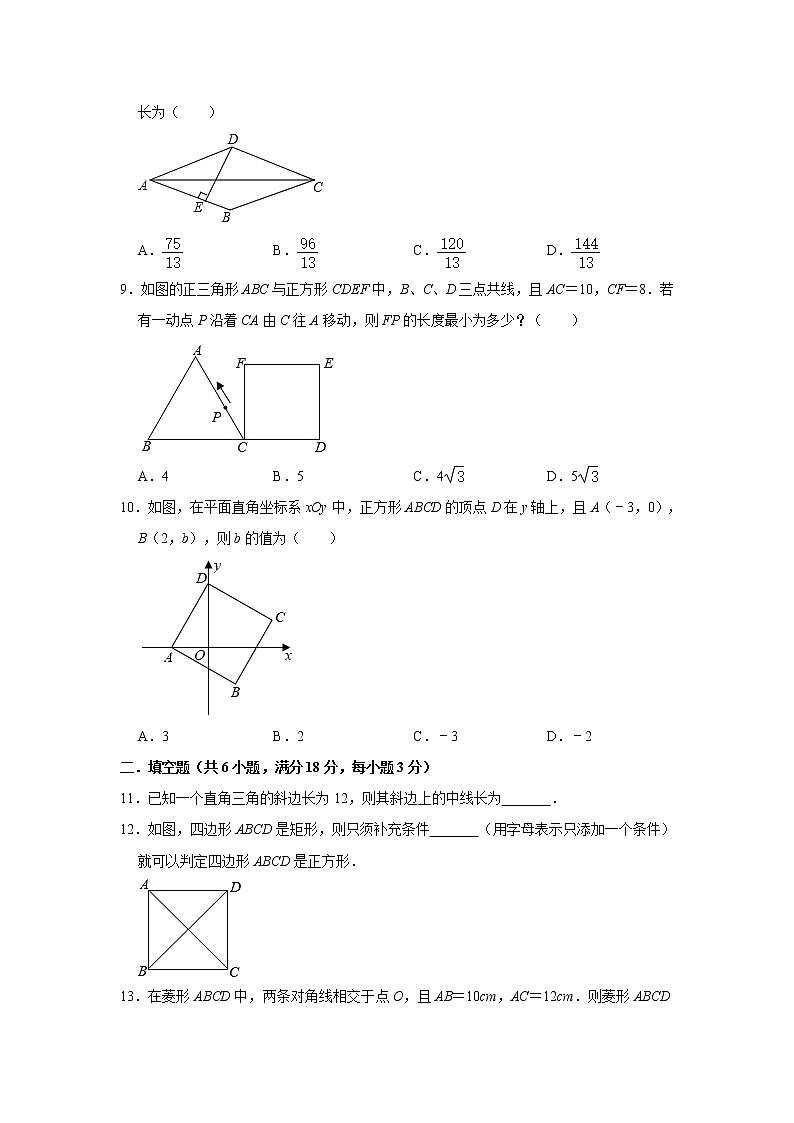
9．如图的正三角形ABC与正方形CDEF中，B、C、D三点共线，且AC＝10，CF＝8．若有一动点P沿着CA由C往A移动，则FP的长度最小为多少？（ ）
A．4B．5C．4D．5
10．如图，在平面直角坐标系xOy中，正方形ABCD的顶点D在y轴上，且A（﹣3，0），B（2，b），则b的值为（ ）
A．3B．2C．﹣3D．﹣2
二．填空题（共6小题，满分18分，每小题3分）
11．已知一个直角三角的斜边长为12，则其斜边上的中线长为 ．
12．如图，四边形ABCD是矩形，则只须补充条件 （用字母表示只添加一个条件）就可以判定四边形ABCD是正方形．
13．在菱形ABCD中，两条对角线相交于点O，且AB＝10cm，AC＝12cm．则菱形ABCD的面积是 cm2．
14．如图，过平行四边形ABCD的对角找BD上一点M分别作平行四边形两边的平行线EF与GH，那么图中的平行四边形AEMG的面积S1与平行四边形HCFM的面积S2的大小关系是 ．
15．如图▱ABCD中，AC与BD交于点O，BD＝2AD，E，F，G分别是OC，OD，AB的中点，下列结论：①FE＝GE；②AE＝GF；③AE⊥GF；④FE⊥GE；⑤∠ADB＝2∠CBE；⑥GF平分∠AGE，其中正确的有 ．
16．在矩形ABCD中，AB＝4，AD＝8，点P为线段AD垂直平分线上一点，且PD＝5，则BP的长是 ．
三．解答题（共7小题，满分52分）
17．（6分）如图，在△ABC中，∠ACB＝90°，CD为AB边上的高，CE为AB边上的中线，AD＝2，CE＝5，求CD的长．
18．（6分）如图，在△ABC中，AC＝BC，点D，E，F分别是AB，AC，BC的中点，连接DE，DF．求证：四边形DFCE是菱形．
19．（7分）如图，在矩形ABCD中，BE⊥AC，DF⊥AC，垂足分别为E、F，连接DE、BF．
（1）求证：BE＝DF；
（2）判断四边形BEDF的形状，并说明理由．
20．（7分）正方形ABCD的边长为6，E，F分别是AB，BC边上的点，且∠EDF＝45°，将△DAE绕点D逆时针旋转90°，得到△DCM．
（1）求证：EF＝CF+AE；
（2）当AE＝2时，求EF的长．
21．（8分）阅读下列材料：如图1，在四边形ABCD中，若AB＝AD，BC＝CD，则把这样的四边形称之为筝形．
（1）如图2，在平行四边形ABCD中，点E、F分别在BC、CD上，且AE＝AF，∠AEC＝∠AFC．求证：四边形AECF是筝形．
（2）如图3，在筝形ABCD中，AB＝AD＝26，BC＝DC＝25，AC＝17，求筝形ABCD的面积．
22．（8分）如图，已知四边形ABCD为正方形，AB＝3，点E为对角线AC上一动点，连接DE，过点E作EF⊥DE，交BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．
（1）求证：矩形DEFG是正方形；
（2）探究：CE+CG的值是否为定值？若是，请求出这个定值；若不是，请说明理由．
23．（10分）如图1，点O是菱形ABCD对角线的交点，已知菱形的边长为12，∠ABC＝60°．
（1）求BD的长；
（2）如图2，点E是菱形边上的动点，连接EO并延长交对边于点G，将射线OE绕点O顺时针旋转30°交菱形于点H，延长HO交对边于点F．
①求证：四边形EFGH是平行四边形；
②若动点E从点B出发，以每秒1个单位长度沿B→A→D的方向在BA和AD上运动，设点E运动的时间为t，当t为何值时，四边形EFGH为矩形．
参考答案
一．选择题（共10小题，满分30分，每小题3分）
1．解：∵四边形ABCD是平行四边形，
∴∠A+∠B＝180°，
∵∠A﹣∠B＝20°，
∴∠A＝100°，
∴∠C＝∠A＝100°．
选：C．
2．解：A．有一个角是直角的四边形不一定是矩形，本选项错误；
B．两条对角线互相垂直的四边形不一定是菱形，本选项错误；
C．两条对角线互相垂直平分的四边形是菱形，本选项错误；
D．两条对角线相等的菱形是正方形，本选项正确．
选：D．
3．解：∵点C，D分别是OA，OB的中点，
∴AB＝2CD＝20（m），
选：C．
4．解：A、“AB＝CD，AD＝BC”是四边形ABCD的两组对边分别相等，可以判定四边形ABCD是平行四边形，本选项错误；
B、由AB∥CD得到∠BAC＝∠DCA，结合∠B＝∠D、AC＝CA可以判定△ABC≌△CDA（AAS），则AB＝CD，根据一组对边相等且平行可以判定四边形ABCD是平行四边形，本选项错误；
C、“∠A＝∠B，∠C＝∠D”是四边形ABCD的两组同旁内角相等，不可以判定四边形ABCD是平行四边形，本选项正确；
D、由∠BAC＝∠ACD可以推知AB∥CD，结合AB＝CD，根据四边形ABCD的一组对边平行且相等，可以判定四边形ABCD是平行四边形，本选项错误．
选：C．
5．解：∵四边形ABCD是平行四边形，
∴AB＝CD，AD＝BC，
∵▱ABCD的周长为24，
∴AB+BC＝12，
∵AB＝4，
∴BC＝8，
选：B．
6．解：如图所示，
根据题意得AO＝×8＝4，BO＝×6＝3，
∵四边形ABCD是菱形，
∴AB＝BC＝CD＝DA，AC⊥BD，
∴△AOB是直角三角形，
∴AB＝＝＝＝5，
∴此菱形的周长为：5×4＝20．
选：A．
7．解：在矩形ABCD中，OA＝OB＝OD，
∵∠AOD＝60°，
∴△AOD是等边三角形，
∴OD＝AD＝1，
∴BD＝1+1＝2，
由勾股定理得，AB＝＝＝．
选：C．
8．解：连接BD交AC于O，
∵四边形ABCD是菱形，
∴AB＝BC＝CD＝AD，
∵菱形ABCD的周长为52，
∴AB＝13，
∵四边形ABCD是菱形，
∴AO＝AC＝12，AO⊥BD，BD＝2BO，
∴BD＝2BO＝2＝2×5＝10，
∴S菱形ABCD＝AC•DB＝×24×10＝120，
∴DE＝，
选：C．
9．解：如图，
过点F，作FM⊥AC交AC于点M，
此时FM为FP的最小值，
∵∠ACD＝60°，∠FCD＝90°，
∴∠FCM＝180°﹣∠ACB﹣∠FCD
＝180°﹣60°﹣90°
＝30°，
又∵∠FMC＝90°，
∴MF＝FC＝4，
即PF的长度最小值为4，
选：A．
10．解：作BM⊥x轴于M．
∵四边形ABCD是正方形，
∴AD＝AB，∠DAB＝90°，
∴∠DAO+∠BAM＝90°，∠BAM+∠ABM＝90°，
∴∠DAO＝∠ABM，
∵∠AOD＝∠AMB＝90°，
在△DAO和△ABM中，
，
∴△DAO≌△ABM（AAS），
∴BM＝OA，
∵A（﹣3，0），B（2，b），
∴BM＝OA＝3，
∴b＝﹣3．
选：C．
二．填空题（共6小题，满分18分，每小题3分）
11．解：一个直角三角的斜边长为12，
∴其斜边上的中线长为×12＝6，
答案为：6．
12．解：因为有一组邻边相等的矩形是正方形，
答案为：AB＝AD（答案不唯一）．
13．解：∵四边形ABCD为菱形，
∴AC⊥BD，OA＝OC＝AC＝6cm，OB＝OD，
∴OB＝＝＝8（cm），
∴BD＝2OB＝16cm，
∴S菱形ABCD＝AC•BD＝×12×16＝96（cm2）．
答案为：96．
14．解：∵四边形ABCD是平行四边形，EF∥BC，HG∥AB，
∴AD＝BC，AB＝CD，AB∥GH∥CD，AD∥EF∥BC，
∴四边形HBEM、GMFD是平行四边形，
在△ABD和△CDB中，
，
∴△ABD≌△CDB（SSS），
即△ABD和△CDB的面积相等；
同理△BEM和△MHB的面积相等，△GMD和△FDM的面积相等，
四边形AEMG和四边形HCFM的面积相等，即S1＝S2．
答案为：S1＝S2．
15．解：①∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC，DO＝BO＝BD，
∵BD＝2AD，
∴AD＝DO，
∴BC＝BO，
∵E是CO中点，
∴BE⊥AC，
∵BC＝BO，
∴△BOC是等腰三角形，
∵E是CO中点，
∴EB⊥CO，
∴∠BEA＝90°，
∵G为AB中点，
∴EG＝AB，
∵四边形ABCD是平行四边形，
∴AB＝CD，
∵E、F分别是OC、OD的中点，
∴EF＝CD，
∴EG＝EF，
①正确；
②连接AF，
Rt△AEB中，G是AB的中点，
∴EG＝AB＝AG，
∵EG＝EF，
∴AG＝EF，
∵E、F分别是OC、OD的中点，
∴EF∥CD，
∵AB∥CD，
∴AG∥EF，
∴四边形AGEF是菱形，
∴AE⊥FG，GF平分∠AGE，
②错误，③⑥正确；
③∵E、F分别是OC、OD的中点，
∴EF∥DC，
∵DC∥AB，
∴EF∥AB，
∴∠EFG＝∠AGF，
∵EF＝EG，
∴∠EFG＝∠EGF，
∴∠EGF＝∠AGF，
∴GF平分∠AGE，③正确；
④由①知：BE⊥AE，
由②、③得：EF∥AB，EF＝CD＝AB＝BG，
∴四边形BEFG是平行四边形，
∵EG＝EF，
∴要使EF⊥GE，则∠EFG＝∠EBA＝∠EAB＝45°，
没有条件AE＝BE，或∠BAC＝45°，④错误；
⑤∵AD∥BC，
∴∠ADB＝∠CBD＝2∠CBE，
∴⑤正确；
本题正确的有：①③⑤⑥．
答案为：①③⑤⑥．
16．解：如图，∵点P在线段AD垂直平分线MN上，
∴MN⊥AD，DM＝AD＝4，MN＝AB＝4，
①点P在矩形外，则P1M＝＝3，
∴P1N＝7，
∴P1B＝＝，
②点P在矩形内，同理P2M＝3，
∴P2N＝1，
∴P2B＝＝，
答案为：或．
三．解答题（共7小题，满分52分）
17．解：∵∠ACB＝90°，CE为AB边上的中线，
∴AB＝2CE＝10，
∴AE＝AB＝5，
∵AD＝2，
∴DE＝3，
在Rt△CDE中，CD＝＝＝4．
18．证明：∵点D，E，F分别是AB，AC，BC的中点，
∴DE∥CF，DE＝BC，DF∥CE，DF＝AC，
∴四边形DECF是平行四边形，
∵AC＝BC，
∴DE＝DF，
∴四边形DFCE是菱形；
19．（1）证明：∵矩形ABCD，
∴AB∥CD，AB＝CD，
∴∠BAE＝∠DCF，
∵BE⊥AC，DF⊥AC，
∴∠BEA＝∠DFC＝90°，
∴△ABE≌△CDF（AAS），
∴BE＝DF．
（2）四边形BEDF是平行四边形．
∵BE⊥AC，DF⊥AC，
∴BE∥DF，
又∵BE＝DF，
∴四边形BEDF是平行四边形．
20．（1）证明：∵△DAE逆时针旋转90°得到△DCM，
∴∠FCM＝∠FCD+∠DCM＝180°，AE＝CM，
∴F、C、M三点共线，
∴DE＝DM，∠EDM＝90°，
∴∠EDF+∠FDM＝90°，
∵∠EDF＝45°，
∴∠FDM＝∠EDF＝45°，
在△DEF和△DMF中，
∵，
∴△DEF≌△DMF（SAS），
∴EF＝MF，
∴EF＝CF+AE；
（2）解：设EF＝MF＝x，
∵AE＝CM＝2，且BC＝6，
∴BM＝BC+CM＝6+2＝8，
∴BF＝BM﹣MF＝BM﹣EF＝8﹣x，
∵EB＝AB﹣AE＝6﹣2＝4，
在Rt△EBF中，由勾股定理得EB2+BF2＝EF2，
即42+（8﹣x）2＝x2，
解得：x＝5，
则EF＝5．
21．解：（1）证明：∵四边形ABCD是平行四边形，
∴∠B＝∠D，
∵∠AEC＝∠AFC，∠AEC+∠AEB＝∠AFC+∠AFD＝180°，
∴∠AEB＝∠AFD，
∵AE＝AF，
∴△AEB≌△AFD（AAS），
∴AB＝AD，BE＝DF，
∴平行四边形ABCD是菱形，
∴BC＝DC，
∴EC＝FC，
∴四边形AECF是筝形．
（2）如图∵AB＝AD，BC＝DC，AC＝AC，
∴△ABC≌△ADC（SSS），
∴S△ABC＝S△ADC，
过点B作BH⊥AC，垂足为H，
在Rt△ABH中，BH2＝AB2﹣AH2＝262﹣AH2，
在Rt△CBH中，BH2＝CB2﹣CH2＝252﹣（17﹣AH）2，
∴262﹣AH2＝252﹣（17﹣AH）2，
∴AH＝10，
∴BH＝＝24，
∴S△ABC＝×17×24＝204．∴筝形ABCD的面积＝2S△ABC＝408．
22．解：（1）如图，作EM⊥BC于M，EN⊥CD于N，
∴∠MEN＝90°，
∵点E是正方形ABCD对角线上的点，
∴EM＝EN，
∵∠DEF＝90°，
∴∠DEN＝∠MEF，
∵∠DNE＝∠FME＝90°，
在△DEN和△FEM中，
，
∴△DEN≌△FEM（ASA），
∴EF＝DE，
∵四边形DEFG是矩形，
∴矩形DEFG是正方形；
（2）CE+CG的值是定值，定值为6，理由如下：
∵正方形DEFG和正方形ABCD，
∴DE＝DG，AD＝DC，
∵∠CDG+∠CDE＝∠ADE+∠CDE＝90°，
∴∠CDG＝∠ADE，
在∴△ADE和△CDG中，，
∴△ADE≌△CDG（SAS），
∴AE＝CG，
∴CE+CG＝CE+AE＝AC＝AB＝×3＝6是定值．
23．解：（1）∵四边形ABCD是菱形，
∴AC⊥BD，∥ABO＝∠OBC＝30°，
∴AO＝AB＝6，
∴OB＝AB•cs30°＝6，
∴BD＝2BO＝12．
（2）①∵四边形ABCD是菱形，
∴AB∥CD，BO＝OD，
∴∠EBO＝∠GDO
∵∠BOE＝∠DOG，
∴△EOB≌△GOD，
∴EO＝GO，同理可得HO＝FO，
∴四边形EFGH是平行四边形．
②a、当点E、H都在AB上时，四边形EFGH是矩形，作∠EOH的平分线OM，
∵OE＝OH，
∴OM⊥EH．
∴∠MOB＝90°﹣∠ABO＝60°，
∵∠MOE＝∠EOH＝15°，
∴∠EOB＝∠MOB﹣∠MOE＝45°，作EN⊥OB于N．设ON＝EN＝x，则NB＝x，
∵OB＝6，
∴x+x＝6，
∴x＝9﹣3，
∴BE＝2EN＝18﹣6，
∴t＝18﹣6时，四边形EFGH是矩形．
b、当点E在AB上，点H在AD上，四边形EFGH是矩形．
由菱形和矩形都是轴对称图形可知，∠AOE＝∠AOH＝15°，
∴∠EOB＝90°﹣15°＝75°，
∵∠ABO＝30°，
∴∠BEO＝180°﹣∠EOB﹣∠ABO＝75°，
∴∠BEO＝∠BOE，
∴BE＝BO＝6，
∴t＝6时，四边形EFGH是矩形．
c、当点E、H都在AD上时，四边形EFGH是矩形．
由b同理可证：DE＝DO＝6，
∴AB+AE＝AB+AD﹣DE＝24﹣6
∴t＝24﹣6时，四边形EFGH是矩形．
d、当点E在AD上，点H在DC上，四边形EFGH是矩形．
由菱形、矩形都是轴对称图形可知，∠DOE＝∠HOE＝15°，
∴∠EOA＝90°﹣15°＝75°，
∵∠OAD＝60°，过点O作OK⊥AD，
∴∠AOK＝90°﹣∠OAD＝30°，
∴∠KOE＝75°﹣30°＝45°，
∴KE＝OK，
∴AE＝AK+KE＝3+3，
∴BA+AE＝15+3，
∴t＝15+3，
∴t＝15+3时，四边形EFGH是矩形．
综上所述，t为18﹣6，6，24﹣6，15+3时，四边形EFGH是矩形．