高考数学三年真题专项汇编卷（2018-2020）考点十五 ：不等式选讲（有答案）

这是一份高考数学三年真题专项汇编卷（2018-2020）考点十五 ：不等式选讲（有答案），共6页。
高考数学三年真题专项汇编卷（2018-2020）考点十五 ：不等式选讲
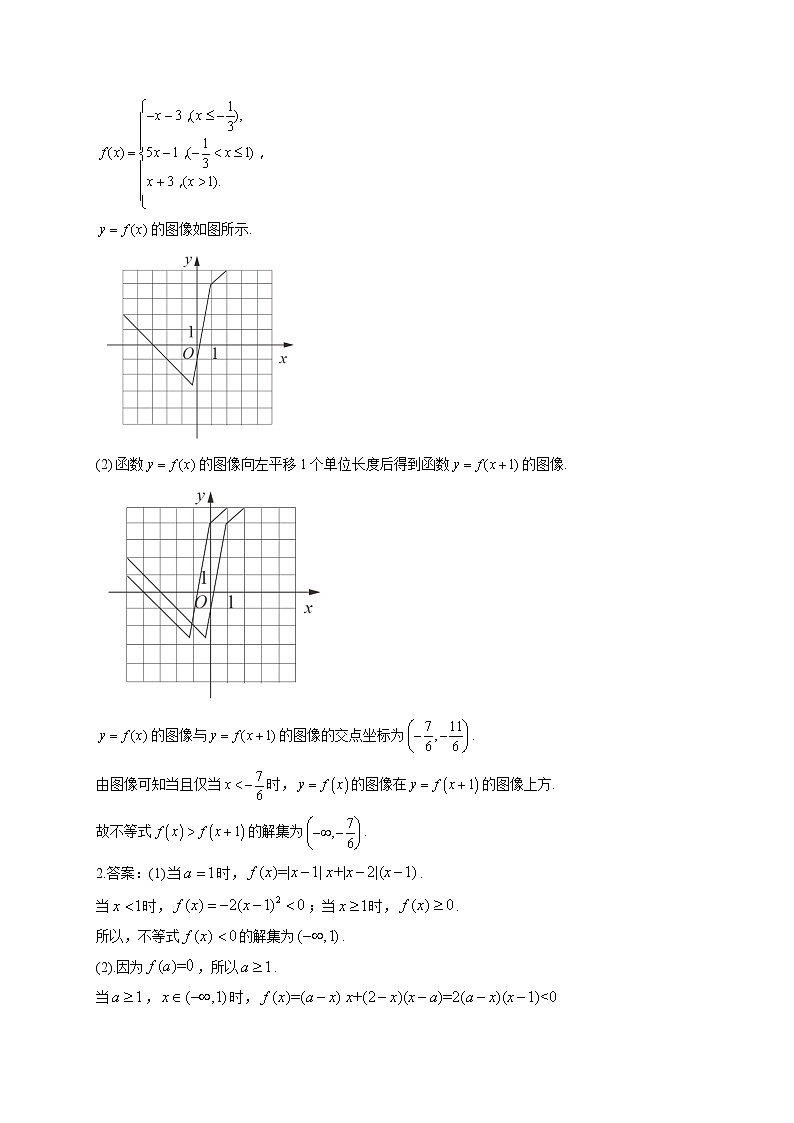
一、解答题1.已知函数.(1)画出的图像；(2)求不等式的解集.2.[选修4-5：不等式选讲] 已知 (1).当时，求不等式的解集；(2).若时，，求的取值范围.3.设a，b，，，.（1）证明：；（2）用表示a，b，c的最大值，证明：.4.已知为正数,且满足.证明：(1).；(2).5.已知函数.（1）当时，求不等式的解集；（2）若，求a的取值范围.6.[选修4-5：不等式选讲] 设，且.(1).求的最小值；(2).若成立，证明：或.7.[选修4—5:不等式选讲]已知    (1).当时,求不等式的解集 (2).若时,不等式成立,求的取值范围 8.[选修4-5:不等式选讲]设函数 (1)当时,求不等式的解集;(2)若,求的取值范围.9.[选修4-5:不等式选讲]设函数    (1)画出的图像;(2)当时, 求的最小值   参考答案1.答案：(1)见解析；(2).解析：(1)由题设知的图像如图所示.(2) 函数的图像向左平移1个单位长度后得到函数的图像.的图像与的图像的交点坐标为.由图像可知当且仅当时，的图像在的图像上方.故不等式的解集为.2.答案：(1).当时，.当时，；当时，.所以，不等式的解集为.(2).因为，所以.当，时，所以，的取值范围是.解析：3.答案：解：（1）由题设可知，均不为零，所以.（2）不妨设，因为，所以.由，可得，故，所以.解析： 4.答案：(1)因为，又，故有.所以.(2)因为为正数且，故有.所以.解析： 5.答案：解：（1）当时因此，不等式的解集为或.（2）因为，故当，即时，.所以当或时，.当时，.所以a的取值范围是.解析：6.答案：(1).由于，故由已知得，当且仅当时等号成立．所以的最小值为.(2).由于，故由已知，当且仅当，，时等号成立．因此的最小值为．由题设知，解得或．解析：7.答案：(1).当时,则∴当时, 即又当时, 满足综上:
(2). 当时成立等价于当时成立.若,则当时;若,的解集为,所以,故.综上,即的取值范围是解析：8.答案：(1)当时, 可得的解集为.
(2)等价于.而,且当时等号成立.故等价于.由可得或,所以的取值范围是.解析：9.答案：(1). ,如下图
(2).由(1)可得: ,当时, 取最小值,∴的最小值为