人教版七年级下册第九章 不等式与不等式组9.1 不等式9.1.2 不等式的性质示范课课件ppt

这是一份人教版七年级下册第九章 不等式与不等式组9.1 不等式9.1.2 不等式的性质示范课课件ppt，共23页。PPT课件主要包含了粉红色的回忆，用“”或“”填空，不等式的性质1，不等式的性质2，不等式的性质3，做一做，言必有“据”等内容，欢迎下载使用。

用不等号（“＜” “＞” “≠” “≥” “≤” ）表示不等关系的式子叫不等式．
（2）什么叫一元一次不等式？
含有一个未知数，未知数的次数是1的不等式，叫做一元一次不等式。
等式两边乘或除以同一个数(除数不为0)，结果仍相等.
等式两边加或减同一个数(或式子)，结果仍相等.
（3）什么叫不等式的解集
含有一个未知数的不等式的所有的解，叫做这个不等式的解集。
等式的性质2 等式两边乘或除以同一个数(除数不为0)，结果仍相等.
等式的性质1 等式两边加或减同一个数(或式子)，结果仍相等.
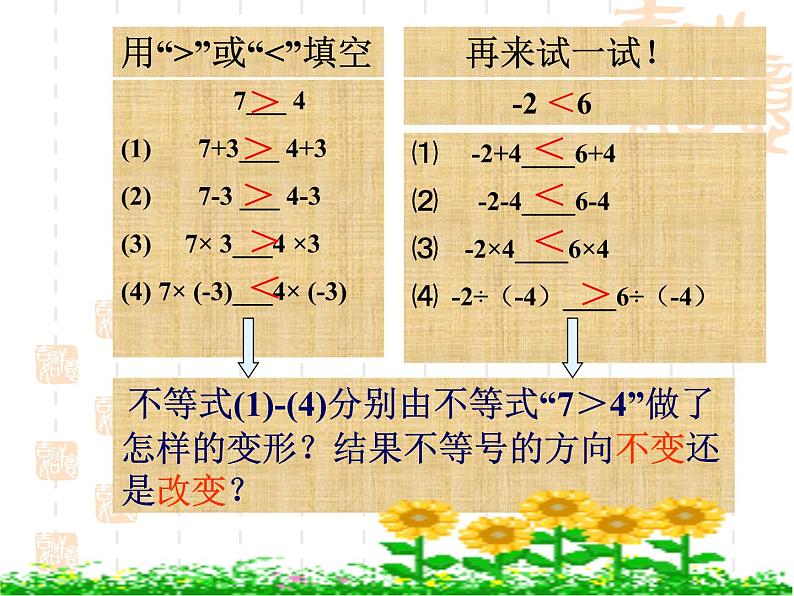
⑴ -2+4____6+4⑵ -2-4____6-4⑶ -2×4____6×4⑷ -2÷（-4）____6÷（-4）
不等式(1)-(4)分别由不等式“7＞4”做了怎样的变形？结果不等号的方向不变还是改变？
再来试一试！
-2 ＜6
用“>”或“<”填空,并总结其中的规律。
不等式的两边加（或减）同一个数(或式子)，不等号的方向不变.
不等式的两边乘（或除以）同一个正数，不等号的方向不变.
不等式的两边乘（或除以）同一个负数，不等号的方向改变.
从刚刚接触的这些不等式中，你能看出一些什么规律吗？
不等式的性质1 不等式两边加或减同一个数(或式子)，不等号的方向不变.
不等式的性质2 不等式两边乘(或除以)同一个正数，不等号的方向不变.
不等式的性质3 不等式两边乘(或除以)同一个负数，不等号的方向改变.
(1)不等式的两边加（或减）同一个数(或式子)，不等号的方向不变.
若a(2) 不等式的两边乘（或除以）同一个正数，不等号的方向不变.
若a0, 则ac(3) 不等式的两边乘（或除以）同一个负数，不等号的方向改变.
等式的两边加（或减）同一个数(或式子)，结果仍相等．
若a=b,则a+c=b+c(或a-c=b-c)
（2）等式的两边乘（或除以）同一个数（除数不能为零），结果仍相等.
若a=b,则ac=bc(或 , c≠0)
不等式、等式性质的异同点.
用“>”或“<”号填空（1）已知a>b,则3a____3b;（2）已知a>b,则-a____-b;（3）已知a>b,则-a+2____-b+2.
解：(1)因为a>b,根据不等式性质2， 两边同时乘以3得 3a>3b.
(2)因为a>b,根据不等式性质3， 两边同时乘以-1得 -a<-b.
小试牛刀
（1）3a 3b；
（2）a-8 b-8
（3）-2a -2b
（4）2a-5 2b-5
（5）-3.5a+1 -3.5b+1
设a>b,用“>”或“<”填空：
设m>n,用 “<“或 “>”填空(1)m-5_____n-5 (2)m+4_____n+4(3)6m_____6n (4)-2m_____-2n
设a>b,用 “< “或”>”填空(1)2a-5______2b-5(2)-3.5b+1_______-3.5a+1
设a＞b，用＜或＞填空
（1）a-3 　　　 b-3；（2）a÷3 　　　 b÷3（3）0.1a 　　　0.1b; (4) -4a 　　　 -4b (5) 2a+3 　　　 2b+3; (6) (m2+1) a 　　(m2+1)b (m为常数)
判断：（1）∵a0 ∴a>0 (5) ∵-a<-3 ∴a<3
已知a<-1,则下列不等式中错误的是( )A.4a<-4 B.-4a<-4 C.a+2<1 D.2-a>3
已知x-3y+2
填空：（1）∵ 2a> 3a ∴a是 数（2）∵ a/2> a/3 ∴a是 数（3） ∵ax1 ∴a是 数
5、由xmy的条件是 ( )A . m≥0 B . m≤0 C. m＞0 D. m＜0６、若mx1,则应为 ( )A. m<0 B. m>0 C. m≤0 D. m≥0７、若m是有理数,则-7m与3m的大小关系应是 ( )A. -7m<3m B. -7m>3m C. -7m≤3m D. 不能确定
　例１　利用不等式的性质解下列不等式．　　(1) x-７＞26 (2) 3x<2x+1 (3) － x﹥50　　(4) -4x﹥3　　　　
(1) x-７＞26
分析：解未知数为x的不等式，就是要使不等式逐步化为x﹥a或x﹤a的形式．解：（１）为了使不等式x-７＞26中不等号的一边变为x，根据不等式的性质１，不等式两边都加７，不等号的方向不变，得 x-７+７﹥26+７ x﹥33
这个不等式的解集在数轴上的表示如图，　　
锋 芒 初 试
(2) 3x<2x+1
3x-2x﹤2x+1-2x x﹤1
这个不等式的解在数轴上的表示如图
注意：解不等式时也可以“移项”，即把不等式的一边的某项变号后移到另一边，而不改变不等号的方向．
这个不等式的解集在数轴的表示如图