北师大版八年级下册2 直角三角形课后测评

北师大版数学八年级下册

1.2《直角三角形》课时练习

一、选择题

1.如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于点E,则有(    )

A.DE=DB            B.DE=AE            C.AE=BE           D.AE=BD

2.已知在△ABC和△DEF中,∠A=∠D=90°,则下列条件中不能判定△ABC和△DEF全等的是(   )

A.AB=DE,AC=DF­              B.AC=EF,BC=DF

­C.AB=DE,BC=EF­              D.∠C=∠F,BC=EF

3.在下列条件中,不能判定两个直角三角形全等的是(    )

A.两条直角边对应相等

B.两个锐角对应相等

C.一个锐角和它所对的直角边对应相等

D.一条斜边和一条直角边对应相等

4.有以下条件：①一锐角与一边对应相等；②两边对应相等；③两锐角对应相等．其中能判断两直角三角形全等的是（        ）

A.①                       B.②                         C.③                        D.①②

5.如图，在Rt△ABC和Rt△A′B′C′中，∠C=∠C′=90°，那么下列各条件中，不能使Rt△ABC≌Rt△A′B′C′的是()

A.AB=A′B′=5，BC=B′C′=3

B.AB=B′C′=5，∠A=∠B′=40°

C.AC=A′C′=5，BC=B′C′=3

D.AC=A′C′=5，∠A=∠A′=40°

6.下列判定两个直角三角形全等的方法中，不正确的是(   )

A.两条直角边分别对应相等

B.斜边和一锐角分别对应相等

C.斜边和一条直角边分别对应相等

D.两个三角形的面积相等

7.如图所示，在数轴上点A所表示的数为a，则a的值为（　　）

A．﹣1﹣      B．1﹣        C．﹣            D．﹣1+

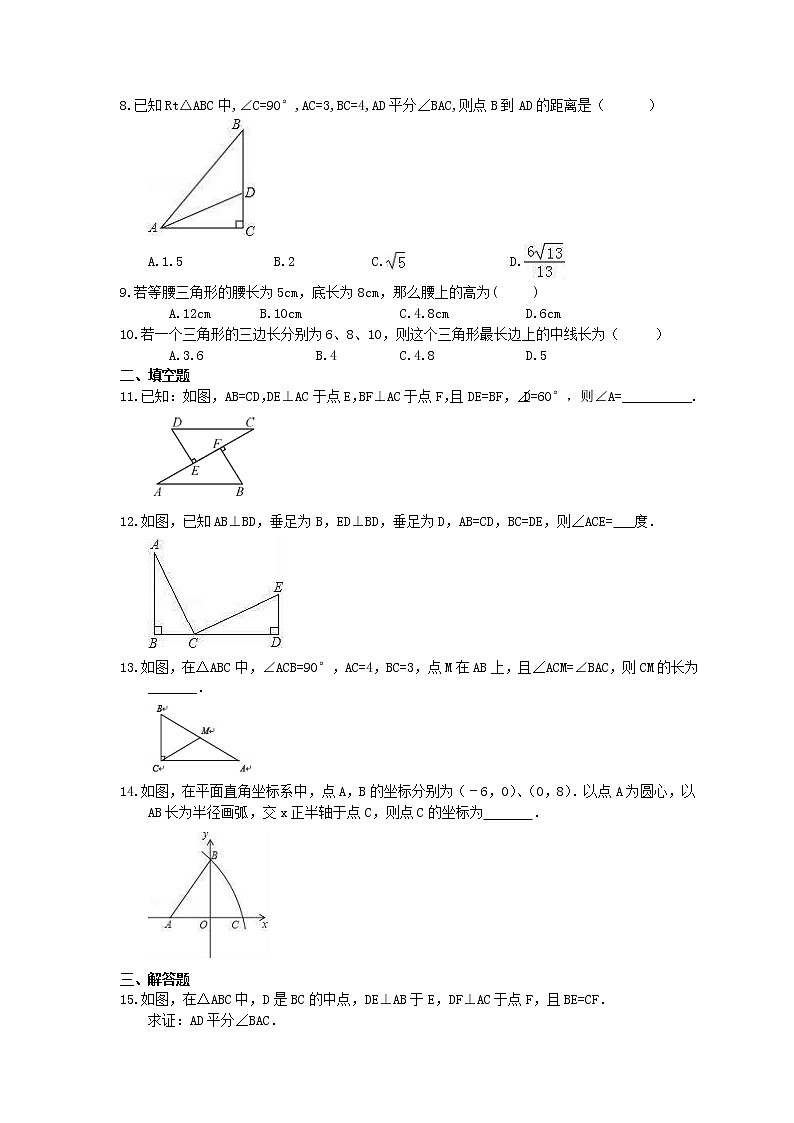
8.已知Rt△ABC中,∠C=90°,AC=3,BC=4,AD平分∠BAC,则点B到AD的距离是（　  　）

A.1.5                           B.2                         C.                             D.

9.若等腰三角形的腰长为5cm，底长为8cm，那么腰上的高为(     )

   A.12cm       B.10cm              C.4.8cm           D.6cm

10.若一个三角形的三边长分别为6、8、10，则这个三角形最长边上的中线长为（     ）

   A.3.6                B.4         C.4.8             D.5

二、填空题

11.已知：如图，AB=CD，DE⊥AC于点E，BF⊥AC于点F，且DE=BF，∠D=60°，则∠A=__________.

12.如图，已知AB⊥BD，垂足为B，ED⊥BD，垂足为D，AB=CD，BC=DE，则∠ACE=   度．

13.如图，在△ABC中，∠ACB=90°，AC=4，BC=3，点M在AB上，且∠ACM=∠BAC，则CM的长为_______．

14.如图，在平面直角坐标系中，点A，B的坐标分别为（﹣6，0）、（0，8）．以点A为圆心，以AB长为半径画弧，交x正半轴于点C，则点C的坐标为　   　．

三、解答题

15.如图，在△ABC中，D是BC的中点，DE⊥AB于E，DF⊥AC于点F，且BE=CF．

求证：AD平分∠BAC．

16.如图，在△ABC中，CD⊥AB于点D，若AC=，CD=5，BC=13，求△ABC的面积.

0.参考答案

1.答案为：B

2.答案为：B

3.答案为：D

4.D

5.答案为：B；

6.答案为：D;

7.A．

8.C．

9.C

10.D

11.答案为：30°。

12.90°．

13.答案为：2.5；

14.答案为：（4，0）．

15.证明：∵D是BC的中点

∴BD=CD，

又∵BE=CF，DE⊥AB，DF⊥AC，

∴Rt△BDE≌Rt△CDF，

∴DE=DF，

∴点D在∠BAC的平分线上，

∴AD平分∠BAC．

16.解：∵CD⊥AB，∴∠CDA=∠BDC=90°

在Rt△ADC中，AD2=AC2﹣CD2，

在Rt△BCD中，BD2=BC2﹣CD2，

∵AC=，CD=5，BC=13，

∴AD==3，BD==12，

∴AB=15，

∴S△ABC=AB•CD=.