





初中数学沪科版七年级下册8.3 完全平方公式与平方差公式教案配套ppt课件
展开多项式与多项式是如何相乘的?
(x + 3)( x+5)
(a+b)(m+n)
①(x + 1)( x-1);②(m + 2)( m-2); ③(2m+ 1)(2m-1); ④(5y + z)(5y-z).
计算下列多项式的积, 你能发现什么规律?
算一算: 看谁算得又快又准.
②(m+ 2)( m-2)=m2 -22;
③(2m+ 1)( 2m-1)=4m2 - 12;
④(5y + z)(5y-z)= 25y2 - z2.
①(x +1)( x-1)=x2 - 1;
想一想: 这些计算结果有什么特点?
(a+b)(a−b)=
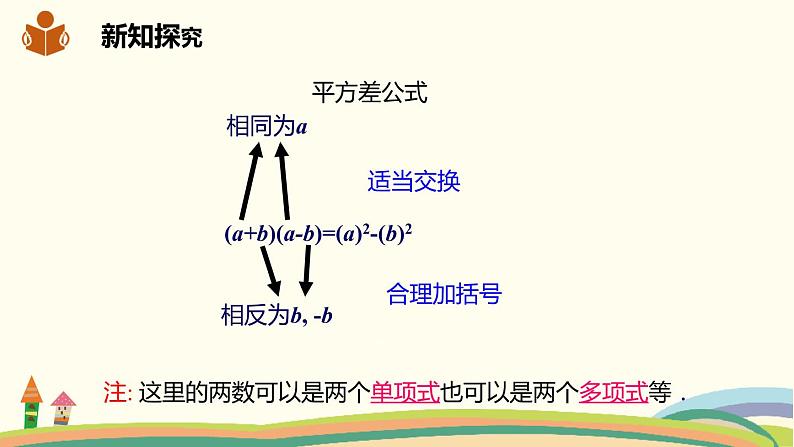
两数和与这两数差的积, 等于这两数的平方差.
1.(a – b ) ( a + b) = a2 - b2
2.(b + a )( -b + a ) = a2 - b2
注: 这里的两数可以是两个单项式也可以是两个多项式等.
(a+b)(a-b)=(a)2-(b)2
(-3+a)(-3-a)
(1+a)(-1+a)
(0.3x-1)(1+0.3x)
练一练: 口答下列各题. (1)(-a+b)(a+b)=_________; (2)(a-b)(b+a)= __________; (3)(-a-b)(-a+b)= ________; (4)(a-b)(-a-b)= _________.
例1 计算:(1)(3x+2 )( 3x-2 ); (2)(-x+2y)(-x-2y).
(2) 原式=(-x)2 - (2y)2
解:(1)原式=(3x)2-22
方法总结: 应用平方差公式计算时, 应注意以下几个问题:(1)左边是两个二项式相乘, 并且这两个二项式中有一项完全相同, 另一项互为相反数; (2)右边是相同项的平方减去相反项的平方; (3)公式中的a和b可以是具体数, 也可以是单项式或多项式.
利用平方差公式计算:(1)(3x-5)(3x+5); (2)(-2a-b)(b-2a);(3)(-7m+8n)(-8n-7m).
解:(1)原式=(3x)2-52=9x2-25.
(2)原式=(-2a)2-b2=4a2-b2.
(3)原式=(-7m)2-(8n)2=49m2-64n2.
例2 计算:(1) 102×98;(2) (y+2) (y-2) – (y-1) (y+5) .
解: (1) 102×98
(2)(y+2)(y-2)- (y-1)(y+5)
=10000 – 4
=(100+2)(100-2)
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1.
计算:(1) 51×49; (2)(3x+4)(3x-4)-(2x+3)(3x-2) .
解: (1) 原式=(50+1)(50-1)
(2) 原式=(3x)2-42-(6x2+5x-6)
= 9x2-16-6x2-5x+6
= 3x2-5x-10.
例3 先化简, 再求值: (2x-y)(y+2x)-(2y+x)(2y-x), 其中 x=1, y=2.
原式=5×12-5×22=-15.
解:原式=4x2-y2-(4y2-x2)
=4x2-y2-4y2+x2
当 x=1, y=2时,
例4 对于任意的正整数n, 整式(3n+1)(3n-1)-(3-n)(3+n)的值一定是10的整数倍吗?
即(3n+1)(3n-1)-(3-n)(3+n)的值是10的倍数.
解:原式=9n2-1-(9-n2)
因为(10n2-10)÷10=n2-1,
所以 n2-1为整数,
方法总结: 对于平方差中的a和b可以是具体的数,也可以是单项式或多项式, 在探究整除性或倍数问题时, 一般先将代数式化为最简, 然后根据结果的特征, 判断其是否具有整除性或倍数关系.
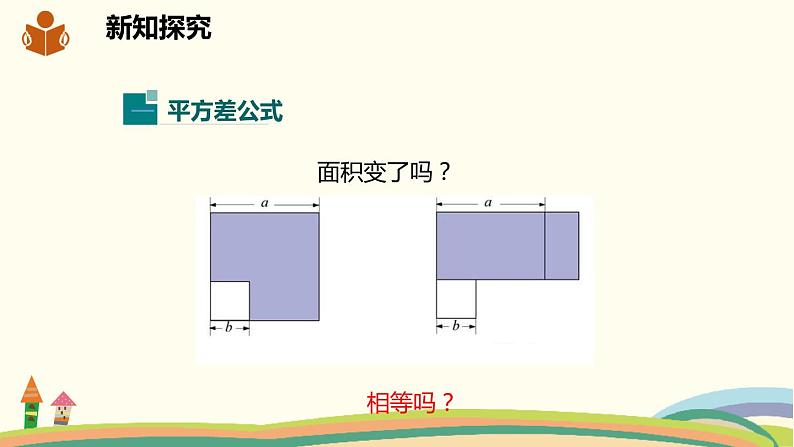
例5 王大伯家把一块边长为a m的正方形土地租给了邻居李大妈. 今年王大伯对李大妈说: “我把这块地一边减少4m, 另外一边增加4m, 继续租给你, 你看如何?” 李大妈一听, 就答应了. 你认为李大妈吃亏了吗? 为什么?
因为a2>a2-16,
理由: 原正方形的面积为a2,
改变边长后面积为(a+4)(a-4)=a2-16.
方法总结: 解决实际问题的关键是根据题意列出算式, 然后根据公式化简算式, 解决问题.
两个数的和与这两个数的差的积, 等于这两个数的平方差
1.符号表示:(a+b)(a-b)=a2-b2
2.紧紧抓住 “一同一反” 这一特征, 在应用时, 只有两个二项式的积才有可能应用平方差公式; 对于不能直接应用公式的, 可能要经过变形才可以应用
1.下列运算中, 可用平方差公式计算的是 ( )A.(x+y)(x+y) B.(-x+y)(x-y)C.(-x-y)(y-x) D.(x+y)(-x-y)
2.计算(2x+1)(2x-1)等于 ( )A.4x2-1 B.2x2-1 C.4x-1 D.4x2+1
3.两个正方形的边长之和为5, 边长之差为2, 那么用较大的正方形的面积减去较小的正方形的面积,差是________.
(1)(a+3b)(a- 3b);
原式=(2a+3)(2a-3)
原式=(-2x2 )2-y2
原式=(a)2-(3b)2
(2)(3+2a)(-3+2a);
(3)(-2x2-y)(-2x2+y).
4.利用平方差公式计算:
5.计算: 20152 - 2014×2016.
20152 - 2014×2016
= 20152 - (2015 - 1)(2015+1)
- (20152 - 12 )
- 20152 + 12
6.利用平方差公式计算:
(1)(a-2)(a+2)(a2 + 4) 原式=(a2-4)(a2+4) =a4-16.
(2) (x-y)(x+y)(x2+y2)(x4+y4).
原式=(x2-y2)(x2+y2)(x4+y4)
=(x4-y4)(x4+y4)
=x8-y8.
7.先化简, 再求值: (x+1)(x-1)+x2(1-x)+x3, 其中x=2.
解:原式=x2-1+x2-x3+x3
原式=2×22-1=7.
8.已知x≠1, 计算: (1+x)(1-x)=1-x2, (1-x)(1+x+x2)=1-x3, (1-x)(1+x+x2+x3)=1 - x4 …(1)观察以上各式并猜想: (1-x)(1+x+x2+…+xn)=________; (n为正整数)
(2)根据你的猜想计算:①(1-2)(1+2+22+23+24+25)=________;②2+22+23+…+2n=________(n为正整数);③(x-1)(x99+x98+x97+…+x2+x+1)=________.
初中数学沪科版七年级下册第8章 整式乘法和因式分解8.3 完全平方公式与平方差公式授课ppt课件: 这是一份初中数学沪科版七年级下册第8章 整式乘法和因式分解8.3 完全平方公式与平方差公式授课ppt课件,共18页。PPT课件主要包含了1a+1b,走近杨辉三角,与数字2的幂的关系,+++,斐波那契数列,杨辉三角的实际应用等内容,欢迎下载使用。
沪科版8.3 完全平方公式与平方差公式教课内容ppt课件: 这是一份沪科版8.3 完全平方公式与平方差公式教课内容ppt课件,共18页。PPT课件主要包含了自主发现,自主探究,p2+2p+1,m2+4m+4,p2-2p+1,m2-4m+4,a2+2ab+b2,a2-2ab+b2,几何解释,−ab等内容,欢迎下载使用。
数学七年级下册8.3 完全平方公式与平方差公式优秀ppt课件: 这是一份数学七年级下册8.3 完全平方公式与平方差公式优秀ppt课件,文件包含832平方差公式课件pptx、832平方差公式教学设计docx、832平方差公式练习题docx等3份课件配套教学资源,其中PPT共18页, 欢迎下载使用。













