2020-2021学年10.2 平行线的判定评课课件ppt

这是一份2020-2021学年10.2 平行线的判定评课课件ppt，共14页。PPT课件主要包含了新课引入，新知探究，应用格式，同位角，内错角，同旁内角，∠1∠2，∠3∠2，∠2+∠4180°，课堂小结等内容，欢迎下载使用。

问题 前面你学了平行线的哪些判定方法？
平行于同一条直线的两条直线平行,即：如果a∥b,c∥b,那么a∥c.
判定方法1：同位角相等，两直线平行.
思考 还有其他判定两条直线平行的方法吗？
问题1 两条直线被第三条直线所截，同时得到同位角、内错角和同旁内角，由同位角相等可以判定两直线平行，那么，能否利用内错角和同旁内角来判定两直线平行呢？
如图，由3 = 2，可推出a//b吗？如何推出？
解： 因为 3= 2（已知）， 1=3(对顶角相等）， 所以 1= 2（等量代换）， 所以 a//b(同位角相等，两直线平行）.
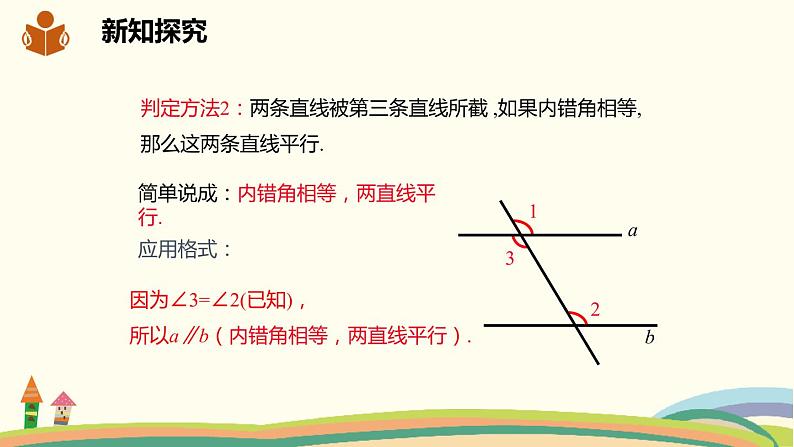
判定方法2：两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
简单说成：内错角相等，两直线平行.
因为∠3=∠2(已知)，所以a∥b（内错角相等，两直线平行）.
例1 如图，BE平分∠ABC，且∠1＝∠2，DE∥BC吗？
解：DE∥BC.理由如下：因为BE平分∠ABC，所以∠1＝∠EBC（角平分线的定义）.又因为∠1＝∠2（已知），所以∠2＝∠EBC（等量代换），所以DE∥BC（内错角相等，两直线平行）.
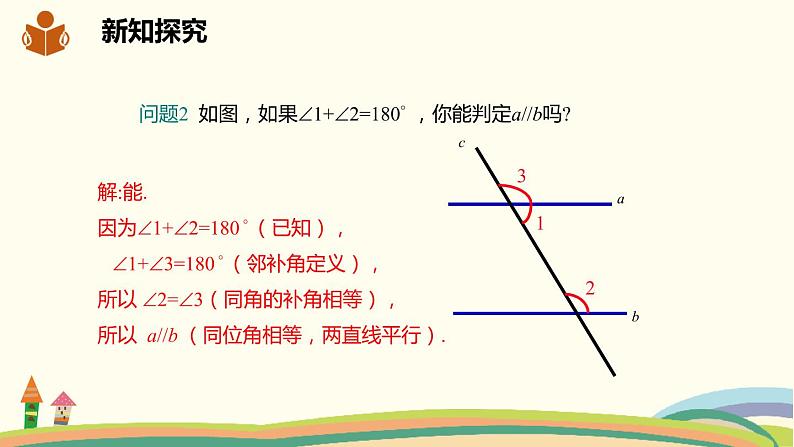
问题2 如图，如果1+2=180° ，你能判定a//b吗?
解:能. 因为1+2=180 ° （已知）， 1+3=180 ° （邻补角定义），所以 2=3（同角的补角相等），所以 a//b （同位角相等，两直线平行）.
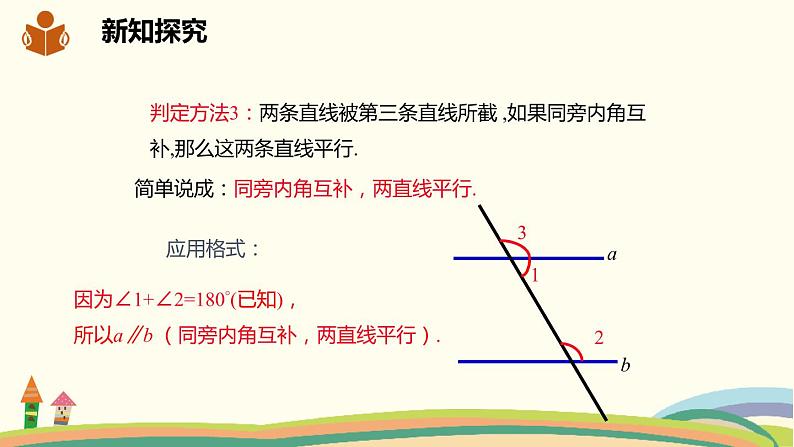
判定方法3：两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
简单说成：同旁内角互补，两直线平行.
因为∠1+∠2=180°(已知)，所以a∥b （同旁内角互补，两直线平行）.
判定两条直线平行的方法
目前学习过的平行线判定的六种方法：①同一平面内,不相交也不重合的两条直线互相平行（平行线的定义）;②如果两条直线都与第三条直线平行,那么这两条直线也互相平行;（传递性）③同位角相等,两直线平行;④内错角相等,两直线平行;⑤同旁内角互补,两直线平行；⑥直线在平移下的像是与它平行的直线；⑦同一平面内,垂直于同一条直线的两条直线互相平行。
1.如图，∠1=30°，∠2或∠3满足条件___________________，则a//b.
∠2＝150°或∠3＝30°
2.如图.（1）从∠1=∠4，可以推出　 ∥ ，理由是 ；
(2)从∠ABC +∠ =180°，可以推出AB∥CD ，理由是 .
内错角相等，两直线平行
同旁内角互补，两直线平行
3. 如图,点A在直线l上,如果∠B = 75°,∠C = 43°,则（1）当 ∠1= 时,直线l ∥BC; （2）当 ∠2= 时,直线l ∥BC.
4.如图,∠ADE =∠DEF, ∠EFC +∠C = 180°, 试问AD与BC平行吗？为什么？
解: 因为∠ADE =∠DEF, 所以AD∥EF (内错角相等,两直线平行).
因为∠EFC +∠C = 180° ,所以BC∥EF (同旁内角互补,两直线平行).
因此 AD∥BC（平行公理的推论或传递性）.