

2021年中考数学三轮冲刺《旋转问题》小题冲刺练习(含答案)
展开一、选择题
如图所示的四个图案中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有( )
A.4个 B.3个 C.2个 D.1个
在平面直角坐标系中,点A的坐标为(1,),以原点为中心,将点A顺时针旋转30°得到点A',则点A'的坐标为( )
A.(,1) B.(,﹣1) C.(2,1) D.(0,2)
如图,Rt△OAB的顶点A(-2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )
A.(eq \r(2),eq \r(2)) B.(2,2) C.(eq \r(2),2) D.(2,eq \r(2))
如图,在直角坐标系中,△ABC的三个顶点都在方格纸的格点上,点A的坐标是(﹣2,0),将△ABC绕点A顺时针旋转90°得到△AB′C′,则点B的对应点B′的坐标是( )
A.(1,﹣1) B.(1,1) C.(﹣1,1) D.(﹣1,﹣1)
如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点 A逆时针旋转75°,得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=6,则AD的长为( )
A.2 B.3 C.2 D.3
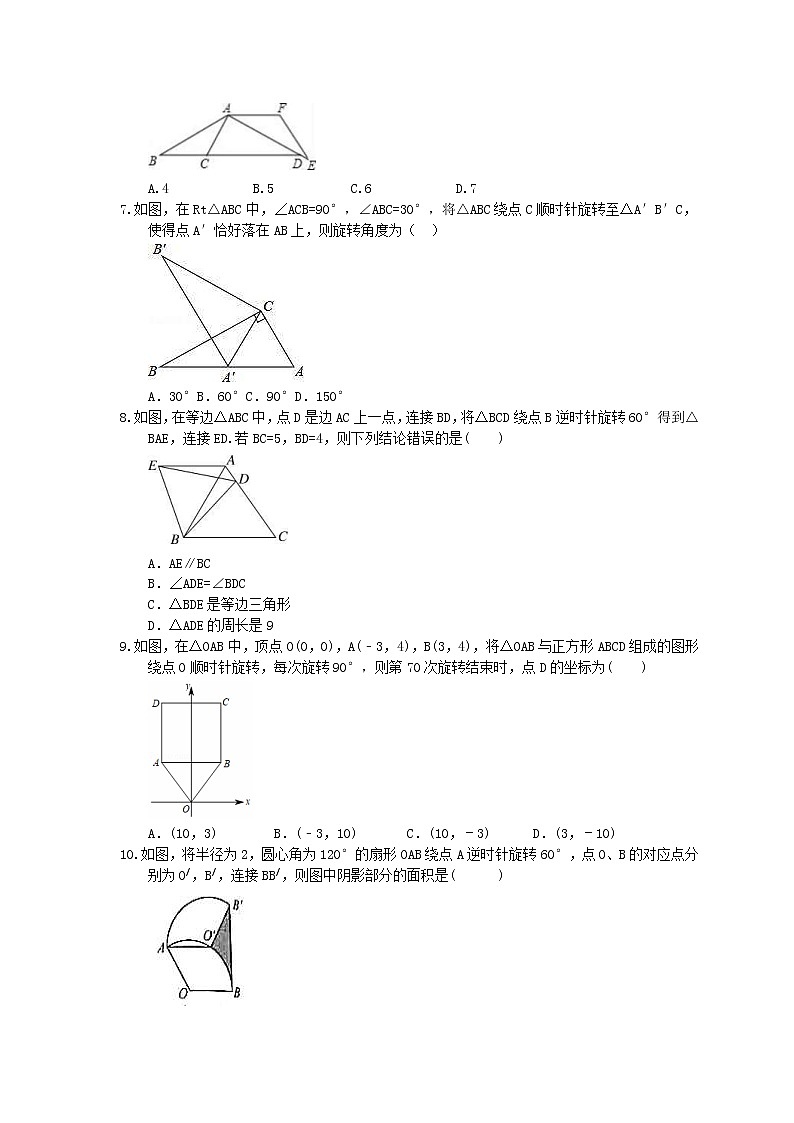
如图,△ABC中,AB=6,BC=4,将△ABC绕点A逆时针旋转得到△AEF,使得AF∥BC,
延长BC交AE于点D,则线段CD的长为( )
A.4 B.5 C.6 D.7
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为( )
A.30°B.60°C.90°D.150°
如图,在等边△ABC中,点D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°得到△BAE,连接ED.若BC=5,BD=4,则下列结论错误的是( )
A.AE∥BC
B.∠ADE=∠BDC
C.△BDE是等边三角形
D.△ADE的周长是9
如图,在△OAB中,顶点O(0,0),A(﹣3,4),B(3,4),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第70次旋转结束时,点D的坐标为( )
A.(10,3) B.(﹣3,10) C.(10,﹣3) D.(3,﹣10)
如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O、B的对应点分别为O/,B/,连接BB/,则图中阴影部分的面积是( )
A. B. C. D.
如图,在△ABC中,∠ACB=90°,将其绕B点顺时针旋转一周,则分别以BA,BC为半径的圆形成一个圆环(阴影部分),为求该圆环的面积,只需测量一条线段的长度即可,这条线段是( )
A.AD B.AB C.AC D.BD
如图,△AOB为等腰三角形,顶点A的坐标(2,),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′坐标为( )
A.(,) B.(,) C.(,) D.(,4)
二、填空题
如图,将△ABC绕着点C顺时针方向旋转50°后得到△A′B′C.若∠A=40°,∠B′=110°,则∠BCA′的度数是________.
如图,香港特别行政区区徽由五个相同的花瓣组成,它是以一个花瓣为“基本图案”通过连续四次旋转组成的,这四次旋转中旋转角度最小是________度.
如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转,CP与量角器的半圆弧交于点E,第24秒,点E在量角器上对应的读数是______度.
如图,将△AOB绕点O逆时针旋转90°,得到△A′OB′.若点A的坐标为(a,b),则点A′的坐标为______.
如图,△ABC中,∠BAC=120°,AD为中线,将AD绕点A顺时针旋转120°得到AE,连接BE,F为AC上一点,连接BF,∠ABE=∠AFB,AF=6,BE=7,则CF的长为 .
如图,正方形ABCD和Rt△AEF,AB=5,AE=AF=4,连接BF,DE.若△AEF绕点A旋转,
当∠ABF最大时,S△ADE= .
\s 0 参考答案
答案为:A
答案为:A.
答案为:C;
A.
D
答案为:B;
B
答案为:B
答案为:D.
答案为:C;
C
C
答案为:80°
答案为:72
答案为:144.
答案为:(﹣b,a).
答案为:8
解:过点D作DH∥BF交AC于点H,过点F作FI⊥BA的延长线于点I,
∵∠BAC=∠EAD=120°
∴∠EAB=DAH,
∵DH∥BF,
∴∠AFB=AHD,
∵∠ABE=∠AFB,
∴∠ABE=∠AHD
在△AEB与△ADH
∴△AEB≌△ADH(AAS)
∴AB=AH,BE=DH=7
设FH=x,
∴AH=AB=6+x,
∵∠FAI=60°,
∴AI=AF=3
由勾股定理可知:IF=3,
∵AD是△ABC的中线,
∴点D是BC的中点,
∵DH∥BF
∴DH是△CBF的中位线,
∴BF=14,
在Rt△BFI中,
由勾股定理可知:(6+x+3)2+(3)2=142
∴x=4
∴CF=2FH=8
答案为:6.
解析:作DH⊥AE于H,如图,
∵AF=4,当△AEF绕点A旋转时,点F在以A为圆心,4为半径的圆上,
∴当BF为此圆的切线时,∠ABF最大,即BF⊥AF,
在Rt△ABF中,BF==3,∵∠EAF=90°,∴∠BAF+∠BAH=90°,
∵∠DAH+∠BAH=90°,∴∠DAH=∠BAF,在△ADH和△ABF中
,∴△ADH≌△ABF(AAS),∴DH=BF=3,
∴S△ADE=AE•DH=×3×4=6.故答案为6.
2021年中考数学三轮冲刺《旋转问题》解答题冲刺练习(含答案): 这是一份2021年中考数学三轮冲刺《旋转问题》解答题冲刺练习(含答案),共12页。
2021年中考数学三轮冲刺《平移问题》小题冲刺练习(含答案): 这是一份2021年中考数学三轮冲刺《平移问题》小题冲刺练习(含答案),共5页。试卷主要包含了选择题,填空题等内容,欢迎下载使用。
2021年中考数学三轮冲刺《最值问题》小题冲刺练习(含答案): 这是一份2021年中考数学三轮冲刺《最值问题》小题冲刺练习(含答案),共5页。试卷主要包含了选择题,填空题等内容,欢迎下载使用。












