

江苏省苏州工业园区2020_2021学年 九年级下学期数学教学调研试卷
展开
这是一份江苏省苏州工业园区2020_2021学年 九年级下学期数学教学调研试卷,共6页。试卷主要包含了05,分式方程的解是等内容,欢迎下载使用。
本试卷由选择题、填空题和解答题三大题组成.共28小题,满分130分.考试时间120分钟.
注意事项:
1.答题前,考生务必将自己的学校、班级、姓名用0.5毫米黑色墨水签字笔填写在答题卡相应位置上,并用0.5毫米黑色墨水签字笔和2B铅笔正确填涂考试号;
2.答选择题必须用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,请用橡皮擦干净后,再选涂其他答案;答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡指定的位置上,不在答题区域内的答案一律无效,不得用其他笔答题;
3.考生答题必须答在答题卡上,保持卡面清洁,不要折叠,不要弄破,答在试卷和草稿纸上一律无效.
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项
是符合题目要求的.请将选择题的答案用2B铅笔涂在答题卡相应位置上.
1.一2的相反数是
A.2 B. C. -2 D.
2.截至2021年4月19日,全国31个省(自治区、直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗约19 500万剂次.19 500万用科学记数法可表示为
A.195 × 106B.19.5 × 107 × 108 × 109
3.下列图形中,可以折叠成三棱柱的是
4.图①是苏州园林内的一种窗棂,图②是这种窗棂中的部分图案,该图案是由1个正六边形和6个全等的等边三角形组成的,则该图案
A.既不是轴对称图形也不是中心对称图形B.是中心对称图形但并不是轴对称图形
C.是轴对称图形但并不是中心对称图形D.既是轴对称图形又是中心对称图形
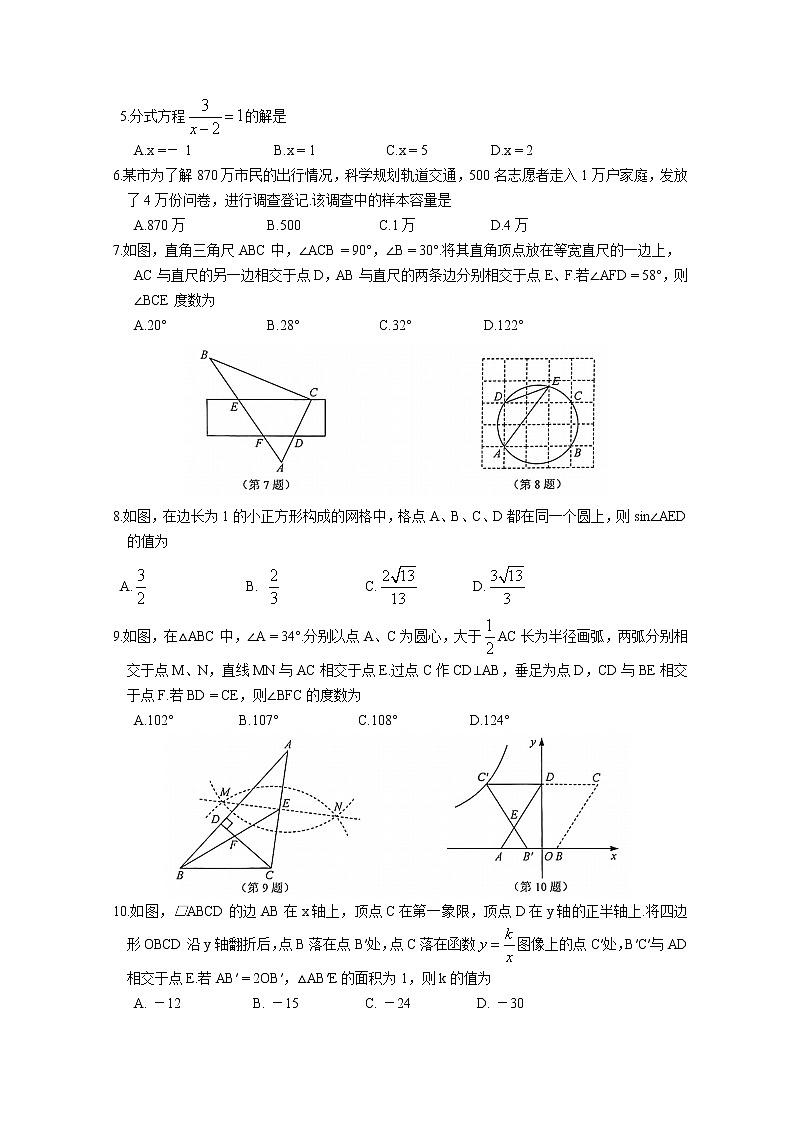
5.分式方程的解是
A.x =- 1 B.x = 1 C.x = 5 D.x = 2
6.某市为了解870万市民的出行情况,科学规划轨道交通,500名志愿者走入1万户家庭,发放了4万份问卷,进行调查登记.该调查中的样本容量是
A.870万 B.500 C.1万 D.4万
7.如图,直角三角尺ABC中,∠ACB = 90°,∠B = 30°.将其直角顶点放在等宽直尺的一边上,
AC与直尺的另一边相交于点D,AB与直尺的两条边分别相交于点E、F.若∠AFD = 58°,则∠BCE度数为
A.20° B.28° C.32° D.122°
8.如图,在边长为1的小正方形构成的网格中,格点A、B、C、D都在同一个圆上,则sin∠AED的值为
A. B. C. D.
9.如图,在△ABC中,∠A = 34°.分别以点A、C为圆心,大于AC长为半径画弧,两弧分别相交于点M、N,直线MN与AC相交于点E.过点C作CD⊥AB,垂足为点D,CD与BE相交于点F.若BD = CE,则∠BFC的度数为
A.102° B.107° C.108° D.124°
10.如图,□ABCD的边AB在x轴上,顶点C在第一象限,顶点D在y轴的正半轴上.将四边形OBCD沿y轴翻折后,点B落在点B′处,点C落在函数图像上的点C′处,B′C′与AD相交于点E.若AB′ = 2OB′,△AB′E的面积为1,则k的值为
A. -12 B. -15 C. -24 D. -30
二、填空题:本大题共8小题,每小题3分,共24分.把答案直接填在答题卡相应位置上.
11.计算: .
12.若在实数范围内有意义,则x的取值范围是_________.
13.底面半径是4 cm,母线长为5 cm的圆锥的侧面积为_________cm2.
14.如图,是用黑白打印机在纸张上打印的边长为20 cm的正方形“易加学院”微课二维码.
为了估计图中黑色部分的总面积,在该二维码内随机掷点,经过大量重复试验,发现点落入
黑色部分的频率稳定在0.75左右,据此可以估计黑色部分的总面积约为_________cm2.
15.元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,弩马日行一百五十里.
驽马先行一十二日,问良马几何日追及之?“如图是两匹马行走路程s(里)关于行走时间t(日)的函数图像,则两个函数图像交点P的坐标是_________.
16.如图①,“东方之门”通过简单的几何曲线处理,将传统文化与现代建筑融为一体,最大程度地传承了苏州历史文化.如图②,“东方之门”的内侧轮廊是由两条抛物线组成的,已知其底部宽度均为80 m,高度分别为300 m和225 m,则在内侧抛物线顶部处的外侧抛物线的水平宽度(AB的长)为_________m.
17.如图,在△ABC中,∠ACB = 90°,AC = 3,BC = 4.将△ABC绕BC的中点D旋转得△EFG,连接CE,则CE的最大值为_________.
18.如图,是小明家客厅地面铺设的瓷砖图案,其中四边形ABCD是正方形,阴影部分是四个全等的菱形,且点A、E、F在同一条直线上.已知菱形较短的对角线长为20 cm,则正方形ABCD的面积为 _________ cm2.
三、解答题:本大题共10小题,共76分.把解答过程写在答题卡相应位置上,解答时应写出必要
的计算过程、推演步骤或文字说明.作图时用2B铅笔或黑色墨水签字笔.
19.(本题满分5分)计算:.
20.(本题满分5分)解不等式组:
21.(本题满分6分)求代数式的值,其中.
22.(本题满分6分)已知:如图,点D在AB上,点E在AC上,AD = AE,BD = CE.
求证:∠B = ∠C.
23.(本题满分8分)甲、乙两人在“定位投篮”选拔赛测试中(共10轮,每轮投10个球)成绩如下:
(1)填表:
(2)如果你是教练,你会选择谁参加正式比赛?请说明理由.
24.(本题满分8分)某单位随机安排甲、乙两人到A、B、C三个社区进行新冠疫苗接种.
(1)甲在A社区接种疫苗的概率是_________;
(2)求甲、乙两人不在同一个社区接种疫苗的概率.
25.(本题满分8分)如图,在苏州工业园区的金鸡湖东岸,有一座世界最大的水上摩天轮“苏州之眼”,其直径为120 m,旋转1周用时24min.小明从摩天轮的底部(与地面相距0.5 m)出发开始观光.
(1)4min后小明离地面多高?
(2)摩天轮转动1周,小明在离地面90.5 m以上的空中有多长时间?
26.(本题满分8分)我们把抛物线上横、纵坐标之和为零的点叫做这条抛物线的“和谐点”(原点除外).
(1)已知抛物线,求其顶点A及“和谐点”B的坐标;
(2)平移抛物线,若所得新抛物线经过点B,且顶点D是新抛物线的“和谐点”,求新抛物线的表达式.
27.(本题满分10分)如图,已知矩形ABCD中,AB = 4,BC = a,点E在边CD上,BE的垂直平分线分别与边AD、BC相交于点F、G.
(1)若四边形BGEF能够成为菱形,则a必须满足的条件是_________;
(2)若a = 6,求AF的最小值;
(3)若经过点D、E、F的圆能够与直线BF、BC同时相切,求a的值.
28.(本题满分12分)
【理解概念】
分别经过两个不相似的直角三角形的直角顶点的两条直线,把这两个直角三角形分别分成两个
小三角形,当一个直角三角形中的一个小三角形与另一个直角三角形中的一个小三角形相似时,
另外两个小三角形也相似,则称这样的两条直线叫做这两个直角三角形的相似分割线.
【巩固新知】
(1)已知:如图①、②,在△ABC和△DEF中,∠ACB = ∠DFE = 90°,∠ACP = ∠D,∠DFQ = ∠A.
①求证:CP、FQ分别是△ABC和△DEF的相似分割线;
②若AC = 6,BC = 8,DF = 8,EF = 4,求AP的长.
【拓展提高】
(2)如图③,AB为⊙O的直径,点C、D在⊙O上,CP、DQ分别是△ABC和△ABD的相似分割线,且△ACP∽△DAQ.
①若点P是AB的黄金分割点,则点Q是否也是AB的黄金分割点?说明理由;②若∠ABC = 30°,AC = 2.当CP⊥DQ时,直接写出AP的长.
相关试卷
这是一份江苏省苏州市苏州工业园区2023-2024学年七年级上学期期末调研数学试卷,文件包含江苏省苏州工业园区2023-2024学年七年级上学期期末调研数学试卷pdf、答案及解析pdf等2份试卷配套教学资源,其中试卷共13页, 欢迎下载使用。
这是一份2023-2024学年江苏省苏州市苏州工业园区数学九年级第一学期期末调研模拟试题含答案,共7页。
这是一份江苏省苏州市苏州工业园区星汇学校2023-—2024学年上学期七年级数学期中调研试卷,共4页。










