2021学年10.4 中心对称教案配套ppt课件

这是一份2021学年10.4 中心对称教案配套ppt课件，共20页。PPT课件主要包含了4中心对称，新课导入，随堂演练，轴对称图形，对称轴，推进新课，课后作业等内容，欢迎下载使用。

10.4 中心对称教学反思
长沈路学校 贾南楠
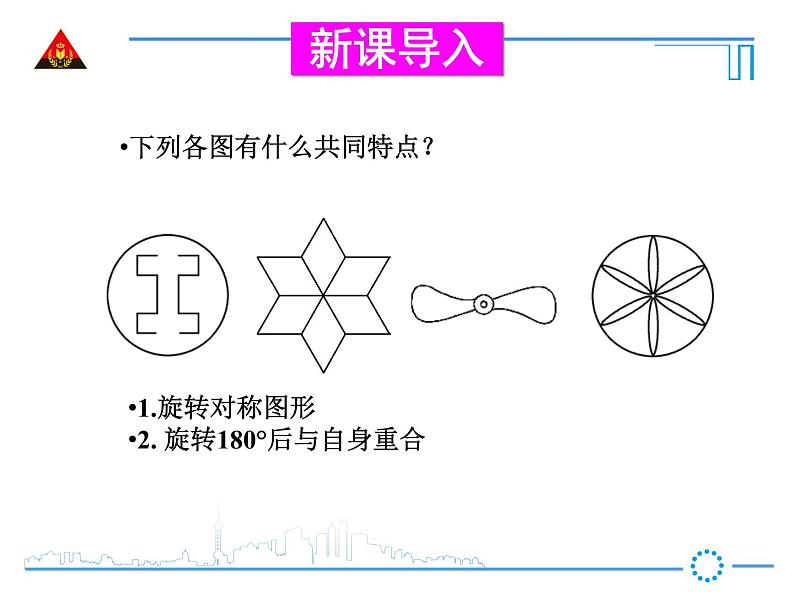
下列各图有什么共同特点？
1.旋转对称图形2. 旋转180°后与自身重合
【归纳结论】 一个图形绕着旋转中心旋转180°后能与自身重合，我们把这种图形叫做中心对称图形，这个中心叫做对称中心.
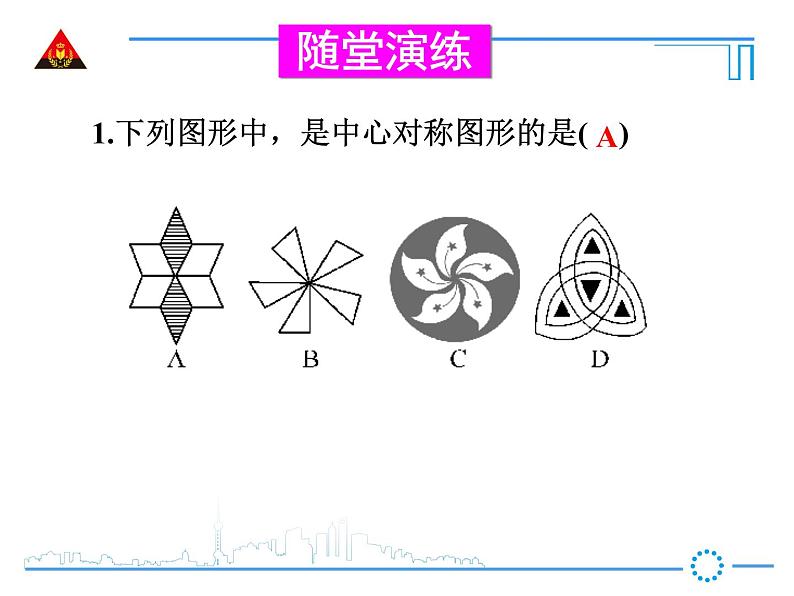
1.下列图形中，是中心对称图形的是( )
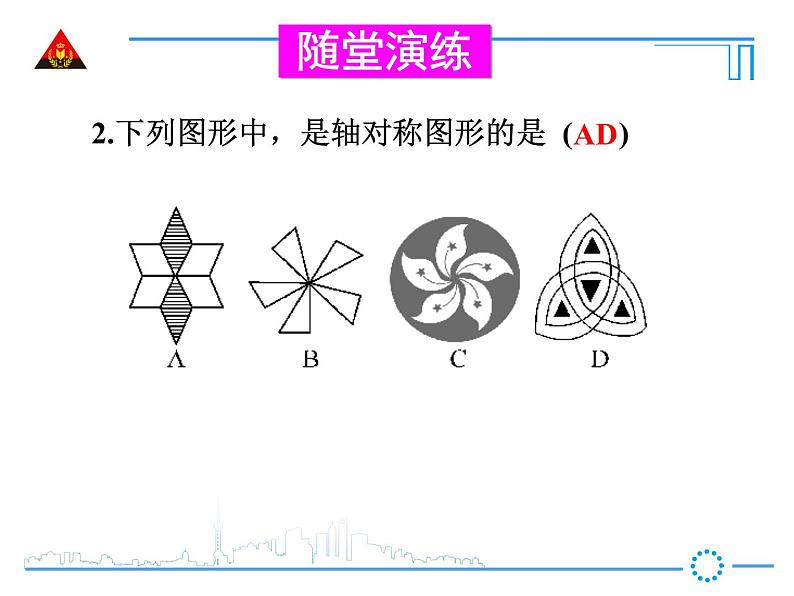
2.下列图形中，是轴对称图形的是 ( )
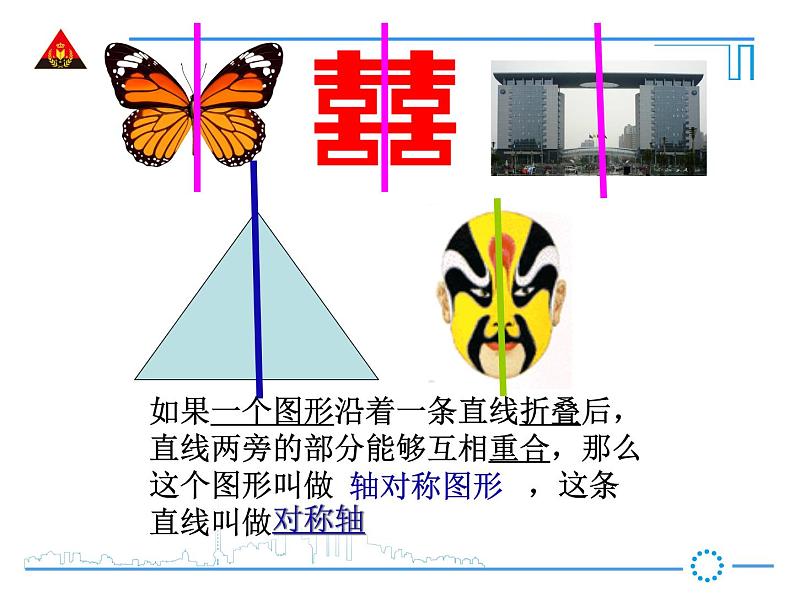
如果一个图形沿着一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做 ，这条直线叫做。
中心对称与轴对称的联系与区别
3.下列多边形中，是中心对称图形而不是轴对称图形的是（ ）A.平行四边形 B.矩形 C.菱形 D.正方形
把一个图形沿着某一条直线翻折过去，如果它能够与另一个图形重合，那么就说这两个图形成轴对称。
D D1
猜想一下，这两个图形是什么关系呢？
【归纳结论】 1.把一个图形绕着某一个点旋180°， 如果它能够和另一个图形重合， 那么就说这两个图形成中心对称。 2.这个点叫做对称中心. 3.这两个图形中的对应点叫做关于中 心的对称点.
4.(P128例）如图，已知△ABC和点O，画出△DEF，使△DEF和△ABC关于点O成中心对称.
分析：中心对称就是旋转180°，关于点O成中心对称就是绕点O旋转180°，因此，我们连AO、BO、CO并延长，取与它们相等的线段即可得到.
解：（1）连结AO并延长AO到D，使OD=OA，于是得到点A的对称点D，如图所示.（2）同样画出点B和点C的对称点E和F.（3）顺次连结DE、EF、FD.则△DEF即为所求的三角形.
5.按下列要求正确画出图形： 已知四边形ABCD和点O，画出四边形ABCD关于点O成中心对称的四边形.
（2）连接AO并延长至A′，使A′O=AO，连接BO并延长至B′，使B′O=BO，连接CO并延长至C′，使C′O=CO，连接DO并延长至D′，使D′O=DO，然后顺次连接即可. 四边形A′B′C′D′如图所示.
1.中心对称图形2.轴对称图形与中心对称图形区别3.成中心对称4.画中心对称图形
1.教材P131习题第1一2题；2.完成练习册本课时的习题.