华师大版七年级下册2 不等式的简单变形教学课件ppt

这是一份华师大版七年级下册2 不等式的简单变形教学课件ppt，共20页。PPT课件主要包含了a+cb+c，a-cb-c，看谁答的快，本节课你学到了什么，课堂小结等内容，欢迎下载使用。

8.2.2 不等式的简单变形
学习目标： 1.通过直观的试验与归纳，自主探索得到不等式的 基本性质. 2.掌握不等式的三条基本性质，会运用不等式的三条性质将不等式进行简单变形. 3.体会求不等式的解与求方程的解的联系与区别，重视数学学习中类比与转化思想的运用. 学习重难点： 学习重点：理解并掌握不等式的性质. 学习难点：正确运用不等式的性质进行不等式的简单变形，特别是性质3的正确应用.
问题：一个倾斜的天平两边分别放有重物砝码，其质量分别为a和b ,从天平实验看a＞ b ,请同学们猜一猜，如果在两边盘内分别放入等质量的砝码c，那么天平会发生什么变化？如果再把砝码c拿出来呢？
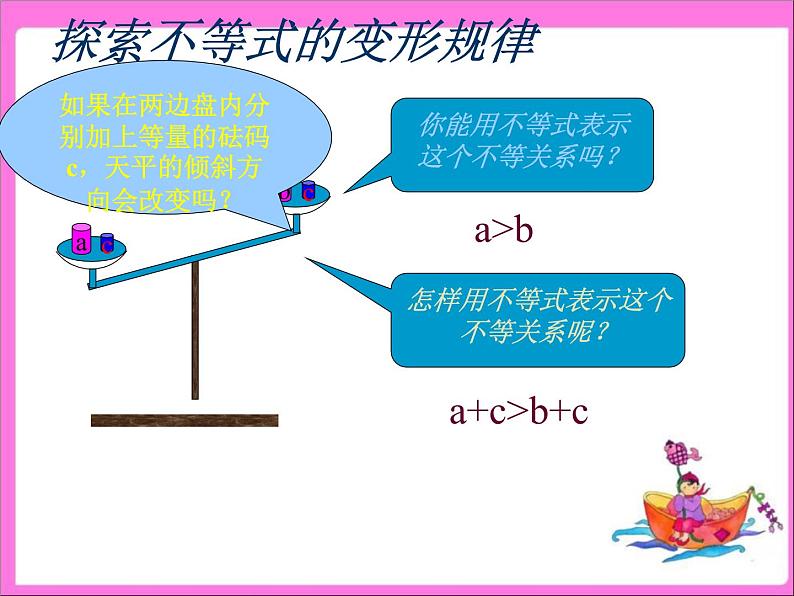
你能用不等式表示这个不等关系吗？
怎样用不等式表示这个不等关系呢？
如果在两边盘内分别加上等量的砝码 c，天平的倾斜方向会改变吗？
用不等式表示这个不等关系.
如果在两边盘内分别减去等量的砝码 c，天平的倾斜方向会改变吗？
根据上述实验你能发现不等式的什么变形规律？
不等式的性质1如果a>b，那么 a＋c>b＋c，a－c>b－c
这就是说，不等式的两边都加上（或减去）同一个数或同一个整式，不等号的方向不变.
与解方程一样，解不等式的过程，就是要将不等式变形成x>a或x(1)不等式的两边都加上7,不等号的方向不变,
x－7＋7<8＋7, 即 x<8+7
(2)不等式的两边都减去2x(即加上－2x),不等号的方向不变，
3x－2x<2x－3－2x 即 3x-2x<-3
这里的变形，与方程变形中的移项相类似，你能说出不等式变形的“移项”该怎么进行吗？
(1)x－7<8(2)3x<2x-3
(1) x－7<8(2) 3x<2x-3
x<8＋7，
合并同类项，得：x<15
合并同类项，得： x<－3
注意：本例的解答也可以整理为如下步骤：
课堂练习 解下列不等式：
不等式的两边都乘以（或除以）同一个数，不等号的方向是否也不变呢 ？
试一试，将不等式7 ＞4两边都乘以同一个数，比较所得的数的大小，用“＜”或“＞”填空：
不等式的性质2如果a＞b，并且c＞0， 那么ac＞bc 不等式的性质3如果a＞b，并且c＜0， 那么ac＜bc
这就是说，不等式两边都乘以（或除以）同一个正数，不等号的方向不变；不等式两边都乘以（或除以）同一个负数，不等号的方向改变.
(1)不等式的两边都乘以2，不等号的方向不变,
得 x>－3
这里的变形，与方程变形中的“将未知数的系数化为1”相类似，它依据的是不等式的性质2或3，要注意不等式两边乘以（或除以）的数是正数还是负数，确定变形时不等号的方向是否需要改变.
课堂练习 解下列不等式：
(1)不等式的两边都加上（或减去）同一个数或同一个整式，不等号的方向不变.
(2)不等式的两边都乘以（或除以） 同一个正数，不等号的方向不变.
(3)不等式的两边都乘以（或除以）同一个负数，不等号的方向改变.
若a⑴ x－ 2＞ 0， x ，⑵ x + 1 ＞ 2， x ， ⑶ 2x ≥ 4， x ，⑷ －3x ≤ 0， x ，⑸ 6－2x ＞0， x .
3.会运用不等式的性质进行 简单变形.
1.不等式的三个性质；
2.不等式性质3中不等号的变 号问题；