吉林省敦化市2020-2021学年八年级下学期期中数学试题1（word版 含答案）

敦化市2020-2021学年度（下）期中测试

八年级数学试卷

一、单选题（共6题；共12分）

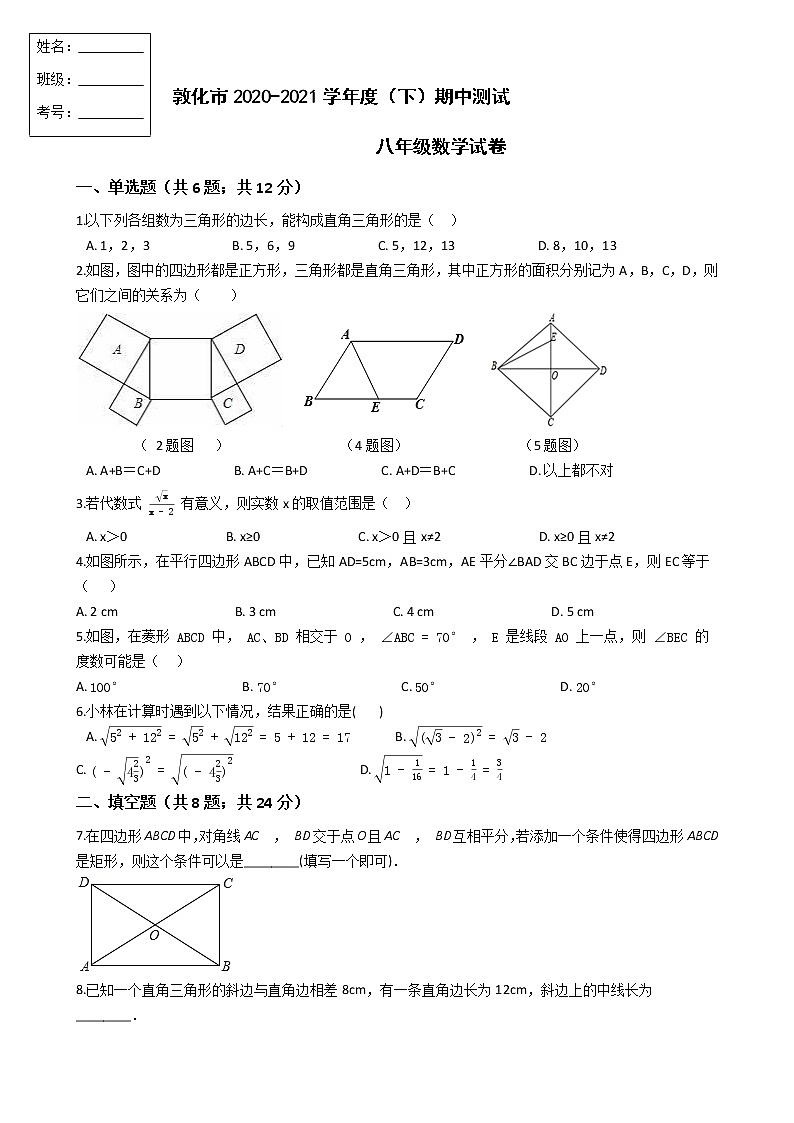
1.以下列各组数为三角形的边长，能构成直角三角形的是（   ）           

A. 1，2，3                          B. 5，6，9                          C. 5，12，13                          D. 8，10，13

2.如图，图中的四边形都是正方形，三角形都是直角三角形，其中正方形的面积分别记为A，B，C，D，则它们之间的关系为（　　） 

（ 2题图   ）                （4题图）                （5题图）

A. A+B＝C+D                      B. A+C＝B+D                      C. A+D＝B+C                      D. 以上都不对

3.若代数式 有意义，则实数x的取值范围是（   ）           

A. x＞0                               B. x≥0                               C. x＞0且x≠2                               D. x≥0且x≠2 

4.如图所示，在平行四边形ABCD中，已知AD=5cm，AB=3cm，AE平分∠BAD交BC边于点E，则EC等于（     ） 

A. 2 cm                                   B. 3 cm                                   C. 4 cm                                   D. 5 cm

5.如图，在菱形 中， 相交于 ， ， 是线段 上一点，则 的度数可能是（    ） 

A.                                    B.                                    C.                                    D.   

6.小林在计算时遇到以下情况，结果正确的是(       )           

A.               B.   

C.                                       D.   

二、填空题（共8题；共24分）

7.在四边形ABCD中，对角线AC  ， BD交于点O且AC  ， BD互相平分，若添加一个条件使得四边形ABCD是矩形，则这个条件可以是________(填写一个即可)． 

8.已知一个直角三角形的斜边与直角边相差8cm，有一条直角边长为12cm，斜边上的中线长为________．   

9.如图，在矩形 中，对角线 与 相交于点 ，垂足为点 ，且 ，则 的长为________.  

（9题图）                (10题图)                     (11题图)

10.如图，每个小正方形的边长为1，四边形的顶点A，B，C，D都在格点上，则线段长度为 的是________. 

 11.如图，在 中， ， 按以下步骤作图： 在 上分别截取 使   分别以 为圆心，以大于 的长为半径作弧，两弧在 内交于点 ③作射线 交 于点 ，则 ________. 

12.已知在数轴上的位置如图所示，化简： =________.

 13.如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，点D在AB上，AD＝AC，AF⊥CD交CD于点E，交CB于点F，则CF的长是________

    （13题图）                               （14题图）

14.如图，对折矩形ABCD，使AB与DC重合，得到折痕EF，将纸片展平再一次折叠，使点D落到G，并使折痕经过点A，已知BC=2.则线段EG的长度为________.

三、简答题（共4题；共20分）

15.计算：       

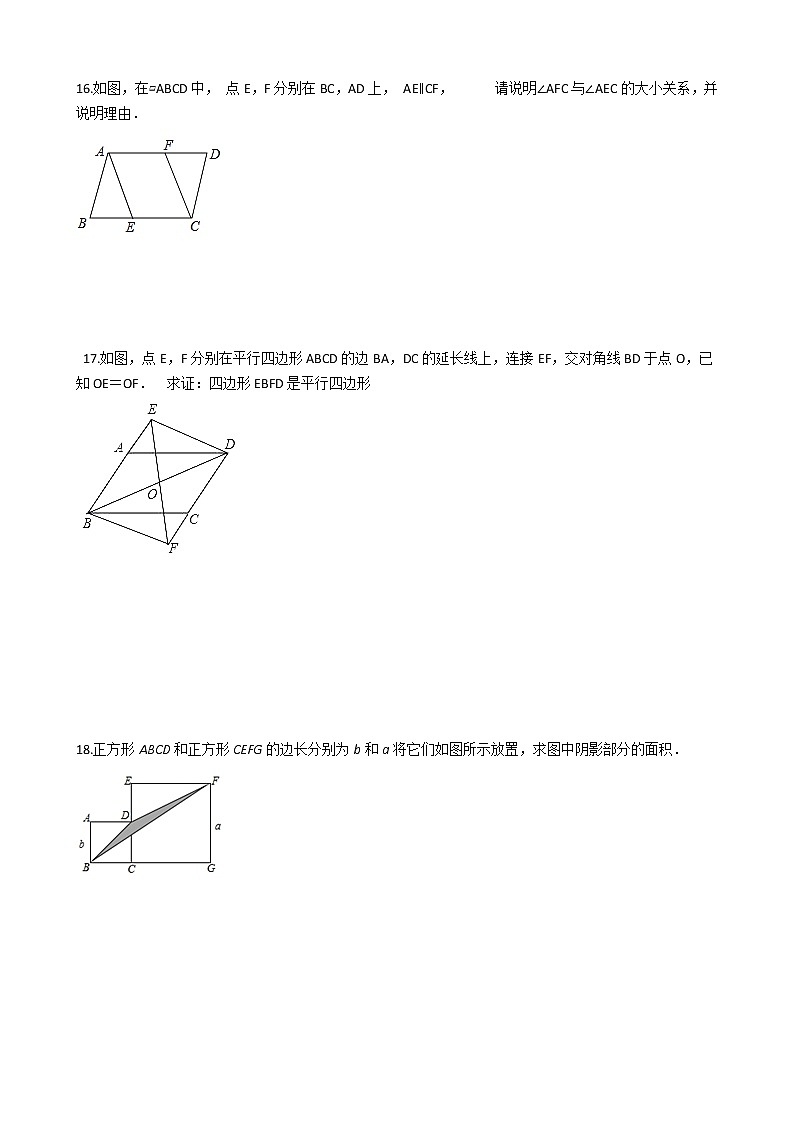
16.如图，在▱ABCD中， 点E，F分别在BC，AD上， AE∥CF，      请说明∠AFC与∠AEC的大小关系，并说明理由．

17.如图，点E，F分别在平行四边形ABCD的边BA，DC的延长线上，连接EF，交对角线BD于点O，已知OE＝OF．  求证：四边形EBFD是平行四边形

18.正方形ABCD和正方形CEFG的边长分别为b和a将它们如图所示放置，求图中阴影部分的面积． 

四、解答题（共4题；共28分）

19.先阅读下列材料，再回答相应的问题

若 与 同时成立，则x的值应是多少？

有下面的解题过程：

由于 与 都是算术平方根，故两者的被开方数 与 均为非负数.而 与 互为相反数，两个非负数互为相反数，只有一种情形，那便是 ， 所以 .

问题：已知 ，求 的值.

20.如图，这是一个供滑板爱好者使用的U型池的示意图，该U型池可以看成是长方体去掉一个“半圆柱”而成，中间可供滑行部分的截面是直径为 的半圆，其边缘 ，点E在 上， ，一滑板爱好者从A点滑到E点，则他滑行的最短距离为多少米？（边缘部分的厚度忽略不计） 

21.如图在 中， ，点E，F分别在 上，求证： . 

22.如图所示，已知 为正方形 外的一点． ， ．将 绕点 顺时针旋转 ，使点 旋转至点 ，且 ，求 的度数． 

五、解答题（共2题；共16+分）

23.如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA边上的中点，阅读下列材料， 

（1）连接AC、BD，由三角形中位线的性质定理可证四边形EFGH是________；   

（2）对角线AC、BD满足条件________时，四边形EFGH是矩形；   

（3）对角线AC、BD满足条件________时，四边形EFGH是菱形；   

（4）对角线AC、BD满足条件________时，四边形EFGH是正方形．   

（5）请你选择以上四个结论中的一个加以证明

24.在一款名为超级玛丽的游戏中，玛丽到达一个高为10米的高台A，利用旗杆顶部的绳索，划过90°到达与高台A水平距离为17米，高为3米的矮台B，试求出玛丽在荡绳索过程中离地面的最低点的高度MN为多少米？ 

六、综合题（共2题；共20分）

25.若一个四边形的两条对角线互相垂直，则称这个四边形为垂美四边形.

（1）概念理解：如图1，在四边形ABCD中， ，判断四边形ABCD是否为垂美四边形，并说明理由；   

（2）性质探究：如图2，试在垂美四边形ABCD中探究 、 、 、 之间的数量关系；   

（3）解决问题：如图3，分别以Rt△ABC的直角边AC和斜边AB为边向外作正方形ACFD和正方形ABGE，连接BD、CE、DE，CE分别交AB、BD于点M、N，若AB＝2，AC＝ ，求线段DE的长.   

26.如图，长方形ABCD中，AB=4cm，BC=6cm，现有一动点P从A出发以2cm/秒的速度，沿矩形的边A—B—C—D回到点A，设点P的运动时间为t秒， 

（1）当t=3秒时，求BP的长；   

（2）当t为何值时，连接BP，AP，△ABP的面积为长方形的面积三分之一？   

（3）Q为AD边上的点，且DQ=5，当t为何值时，以长方形的两个顶点及点P为顶点的三角形与△DCQ全等？   

答案解析部分

一、单选题

1.【答案】C  2.【答案】 A   3.【答案】 D   4.【答案】 A   5.【答案】 B   6.【答案】 C  

二、填空题

7.【答案】 AC=BD或四边形ABCD有1个内角等于90度．   8.【答案】 10cm或   

9.【答案】 3    10.【答案】 AB   11.【答案】    12.【答案】 2n-2m-1   13.【答案】 1.5  

14.【答案】   

三、计算题

15.【答案】 （1）解：原式    

；

四、解答题

16.【答案】解：∠AFC=∠AEC，  理由如下：∵平行四边形ABCD中，BC∥AD，
又AE∥CF，
∴四边形AECF为平行四边形，
∴∠AEC=∠AFC 

17.【答案】 证明：∵四边形ABCD是平行四边形 

∴AB∥CD

∴∠BEO=∠DFO，且∠BOE=∠DOF，EO=FO

∴△BEO≌△DFO（ASA）

∴BE=DF，且BE∥DF

∴四边形BEDF是平行四边形

18.【答案】 解：由题意得： 

19.【答案】 解：由于 与 都是算术平方根，

故两者的被开方数 与 均为非负数，

而 与 互为相反数，两个非负数互为相反数，只有一种情形，那便是 ， ，

所以 ，y=2，

代入即可得 = = .

20.【答案】 解：如图是其侧面展开图：AD=π• =20，AB=CD=20.DE=CD-CE=20-5=15，  

在Rt△ADE中，AE= = =25.

故他滑行的最短距离约为25米.

21.【答案】 证明：    

，均为直角三角形

在 中，

在 中，

在 中，

在 中，

22.【答案】 解：连接 ，  

∵ 绕点 顺时针旋转 得△CBP′，

∴ ，∠PBP′=90°，

∠BPP′=∠BP′P=45°，

在Rt△PBP′中，

由勾股定理

，

∵ ，

即 ，

∴△ 是直角三角形，

∴ ，

∴ ，

，

，

∴ ．

23.【答案】 （1）平行四边形
（2）AC⊥BD
（3）AC=BD
（4）AC⊥BD且AC=BD  

24.【答案】 解：作AE⊥OM，BF⊥OM，垂足分别为E、F，如图： 

由题意： ，∠AOB=90°，

∵∠AOE+∠BOF=∠BOF+∠OBF=90°，

∴∠AOE=∠OBF，

在△AOE和△OBF中，

，

∴△AOE≌△OBF（AAS），

∴OE=BF，AE=OF，

即OE+OF=AE+BF=CD=17（米）

∵EF=EM-FM=AC-BD=10-3=7（米），

∴EO+OE+OF=17（米），

∴OE=5米，OF=12米，

∴OM=OF+FM=15米，

又因为由勾股定理得ON=OA= =13（米），

∴MN=15-13=2（米）.

答：玛丽在荡绳索过程中离地面的最低点的高度MN为2米.

五、综合题

25.【答案】 （1）解：如图1，四边形ABCD是垂美四边形.

理由如下：

证法一：

∵ ，AC＝AC，

∴△ABC≌△ADC.

∴∠BAC＝∠DAC.

∴AC是等腰三角形ABD顶角∠BAD的平分线.

∴ .

∴四边形ABCD是垂美四边形.

证法二：

连结AC、BD交于点E.

∵ ，

∴点A在线段BD的垂直平分线上.

∵ ，

∴点C在线段BD的垂直平分线上.

∴直线AC是线段BD的垂直平分线.

∴ .

∴四边形ABCD是垂美四边形.

（2）解：如图2，在垂美四边形ABCD中，

∵ 于点O，

∴∠AOB＝∠BOC＝∠COD＝∠AOD＝90°.

∴ .

.

.

.

∴ .

.

∴ .

（3）解：分别连结CD、BE，

如图3，∵∠CAD＝∠BAE＝90°，

∴ .

即 .

在 和 中，

，

∴ .

∴ .

∵∠BAE＝90°，

∴ .

∴ .

∴ ，即 .

∴四边形CDEB是垂美四边形.

由（2）得： .

∵AB＝AE＝2，AC＝AD＝ ，

∴ .

.

.

∴ .

∴ .

26.【答案】 （1）解：当t=3秒时， 

点P走过的路程为： ，

∵AB=4，

∴点P运动到线段BC上，

∴BP=6-4=2

（2）解：∵矩形ABCD的面积= ，  

∴△ABP的面积= ，

∵AB=4，

∴△ABP的高为： ，

如图：

当点P在BC上时，有BP=4，

∴时间为： s；

当点P在AD上时，有AP=4，

∴时间为： s；

∴当时间t=4s或t=8s时，△ABP的面积为长方形的面积三分之一

（3）解：根据题意，如图，连接CQ，有AB=CD=4，∠A=∠B=∠C=∠D=90°，DQ=5， 

∴要使得一个三角形与△DCQ全等，则另一直角边必须等于DQ.

①当点P运动到P1时，CP1=DQ=5，此时△DCQ≌△CDP1  ，

∴点P的路程为：AB+BP1=4+1=5，

∴时间 ；

②当点P运动到P2时，BP2= DQ=5，此时△CDQ≌△ABP2  ，

∴点P的路程为：AB+BP2=4+5=9，

∴时间 ；

③当点P运动到P3时，AP3= DQ=5，此时△CDQ≌△ABP3  ，

∴点P的路程为：AB+BC+CD+DP3=4+6+4+1=15，

∴时间 ；

④当点P运动到P4时，即P与Q重合时，DP4=DQ=5，△CDQ≌△CDP4  ，

∴点P的路程为：AB+BC+CD+DP4=4+6+4+5=19，

∴时间 ；

综合上述，时间t的值可以是：t=2.5秒，4.5秒，7.5秒或9.5秒.