2021年重庆市中考二轮复习第23题函数图像专练专题（四）

2021年重庆考二轮复习第23题

函数图像专练:专题 (四)

1.学习函数时，我们经历了列表，描点，连线画出函数图象，观察分析图象特征，概括函数性质的过程.结合已有的学习经验，下面我们对函数y=||展开探索，请将以下探索|x+2 |过程补充完整:

(1)选取适当的值补全表格;描点，连线，在所给的平面直角坐标系中画出函数y=||的图象.

(2)写出函数y=||的一条性质:           ;

(3)结合函数图象，请直接写出y=||=-x+2的解:         ( 结果保留1位小数，误差不超过0.2).

2.数学活动:

问题情境:有这样一个问题:探究函数y=+1的图象与性质，小明根据学习函数的经验，对函数y=+1的图象与性质进行了探究.问题解决:下面是小明的探究过程，请补充完整:

(1)函数y=+1的自变量x的取值范围是           .

(2)表是y与x的几组对应值.

求m的值;

(3)如图，在平面直角坐标系中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象.

(4)结合函数的图象，写出该函数的性质(两条即可)

3.小林在学习完一次函数与反比例函数的图象与性质后，对函数图象与性质研究饶有兴趣,便想着将一次函数与反比例函数的解析式进行组合研究.他选取特殊的一次函数y=k1x (k1≠0)与反比例函数y=(k2≠0)，相加后，得到一个新的函数y=k1x+(k1,k2≠0).已知，这个新函数满足:当x=时，y=;当x=时，y=

(1)求出小林研究的这个组合函数的解析式;

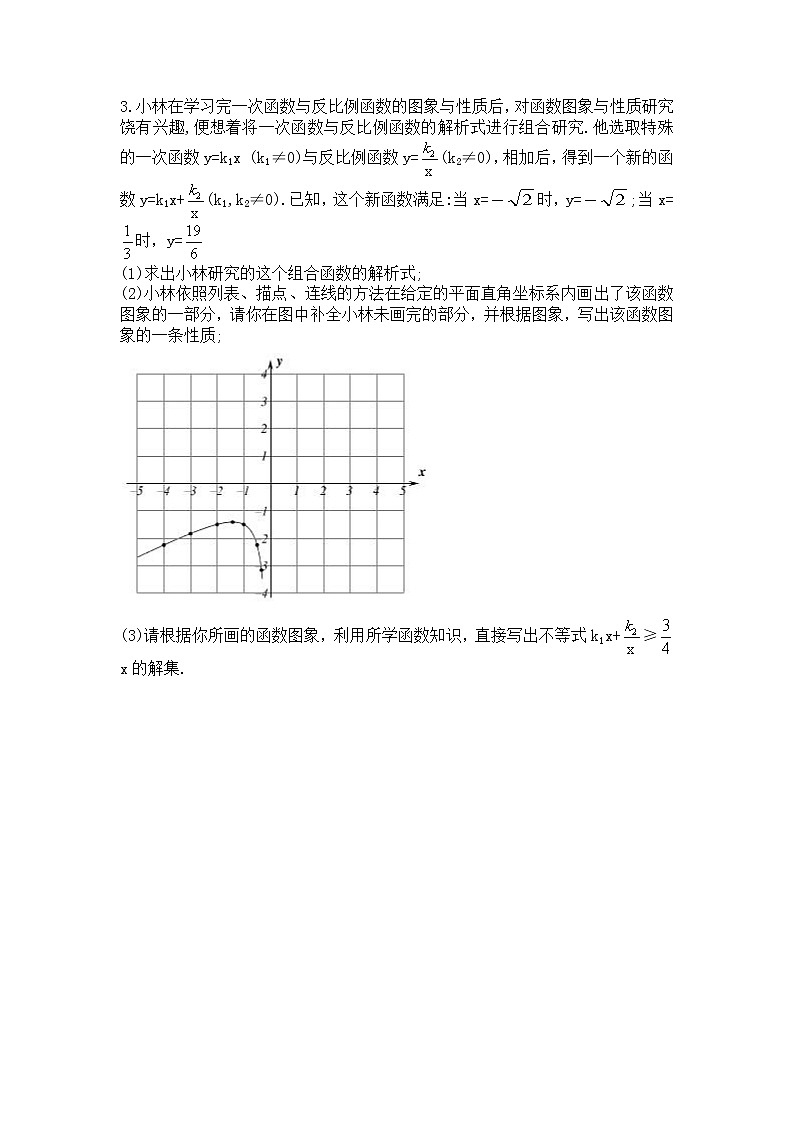
(2)小林依照列表、描点、连线的方法在给定的平面直角坐标系内画出了该函数图象的一部分，请你在图中补全小林未画完的部分，并根据图象，写出该函数图象的一条性质;

(3)请根据你所画的函数图象，利用所学函数知识，直接写出不等式k1x+≥x的解集.

4.已知函数y=|-b|，其中b>0，当x=3时，y=0;当x=0时，y=3;

(1)根据给定的条件，则a=        ，b=           .

(2)在给出的平面直角坐标系中，画出函数图像;

(3)①结合所画的图像，直接写出方程x+3=|-b|的解,解为         .(精确到十分位).

②若--次函数y=kx+3的图像与y=|-b|的图像有且只有三个交点,则k的取值范围是                     .

5.已知函数y=，方程y-a=0有三个根，且x1<x2<x3;

(1)在右图坐标系中画出函数y的图像，并写出a的取值范围;

(2)求x1+x2+x3;的取值范围.

6.某数学兴趣小组的同学在研究函数y=+1的图象时，先对函数y=的图象进行了如下探索.

(1)①列表:列出,与x的几组对应值如下:

②描点:根据表中数据描点如图所示;

③连线:请在图中画出函数y= 的图象;

④观察图象，写出两条关于该函数的性质.

(2)根据以.上探究结果,完成下列问题:

①函数y=+1中，自变建x的取值范围为                         ;

②函数y=+1的图象可由函数y=的图像经过怎样的变换得到?

③写出两条关于函数y=+1的性质;

④直接写出不等式+1＞2的解集.

7.有这样一个问题:探究函数y=+x的图象与性质，张聪根据学习函数的经验对函y=+x“的图象与性质进行了探究，下面是张聪的探究过程，请补充完整:

(1)函数y=+x中自量x的取值范围是                       .

(2)是y与的几组对应值，请直接写出m的值                   .

(3)在平面直角坐标系x0y中，描出了以上表中各对应值为坐标的点，根据描出的点，画出该函数的图象;

(4)根据画出的函数图象，发现下列特征:

①该函数的图象是中心对称图形,对称中心的坐标是                  .

②该函数的图象与直线x=2越来越事近而永不相交,读函数的图象还与          .直线越来越靠近而永不相交.

8.已知常数a (a是整数)满足下面两个要求:

①关于x的一元二次方程ax2+3x-1=0有两个不相等的实数根;

②反比例函数y=的图象在二，四象限.

(1)求a的值;

(2)在所给直角坐标系中用描点法画出y=的图象，并根据图象写出:当x>4时，y的取值范围;当y<1时，x的取值范围是.

9.某班数学兴迎小组根据学习函数的经验，通过列表、描点、连线的方法对函数y=的图象与性质进行了研究，研究过程如下，请补充完整.

(1) y与x的几组对应值如下表:

函数y=的自变量x的取值范围是            ，m的值为             ；

(2)在给出的平面直角坐标系中，描出以上表中各组对应值为坐标的点,画出函数y=的大致图象，并写出该函数的两条性质;

(3)在同一坐标系中画出函数y1=x的图象，并根据图象直接写出当y>y1时，自变里x的取值范围.

10.有这样一个问题:探究函数y=x-1+的图象与性质.下面是小东的探究过程，请补充完成:

(1)函数y=x-1+的自变量x的取值范围是                  .

(2)在平面直角坐标系xOy中描出了图象上的一些点，请你画出函数的图象;下表是y与x的几组对应值.

(3)求m的值;

(4)根据图象写出此函数教的一条性质.

11.问题呈现:我们知道板比例函数y=(x＞0)的图象是双曲线，那么函数y=+n(k、m、n为常数且k≠0)的图象还是双曲线吗?它与反比例函数y=(x＞0)的图象有怎样的关系呢?让我们一起开启探索之旅....

探索思考:我们可以值鉴以前研究函数的方法，首先探索函数y=的图象.

(1)填写下表，并画出函数y=的图象.

①列表:

②描点并连线.

（2）观察图象，写出该函教图象的两条不同类型的特征:①        ②        

理解运用:函数y=的图象是由团数y=的图象向       平移      一个单位，其对称中心的坐标为                            .

灵活应用:根据上述画函图象的经验，想一想函数y=+2的图象大致位置，并根据图像指出，当x满足         时，y≥3.

12.已知函数y=+b(a 、b为常数且a≠0)中，当x=2时，y=4;当x=-1时，y=1.请对该函数及其图像进行如下探究:

(1)求该函救的解析式，并直接写出该函数自变重x的取值范围：

(2)请在下列直角坐标系中画出函数的图像：

列表如下:

描点连线：

(3)请结合所画函教图象，写出函数图象的两条性质

(4)请你在上方直角坐标系中画画出函数y=2x的图像，结合上述函数的图像，写出不等式.+b≥2x的解集.

13.某班数学兴遇小组对函数y=x2-2|x|-3的图象和性质进行了探究，探究过程如下，请补充完整:

(1)自变量x的取值范围是全体实数，x与y”的几组对应值如下:

其中，m=                .

(2)根据表中数据,在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请画出该函数图象的另一部分.

(3)观察函数y=x2-2|x|-3图象，回答下列问题:

①函数图像的对称性是:                 .

②当x>0时，写出y随x的变化规律:                 .

(4)进一步探究函数图象发现:方程x2-2|x|-3=-3有       个实数根.

14.某班“数学兴趣小组对函数y=-x2+2|x|+1 的图象和性质进行了探究，探究过程如下，请补充完整.

(1)自变量x的取值范围是全体实数，x与y的几组对应值列表如下:

其中，m=               .

(2)根据上表数据，在如图所示的平面直角坐标系中描点，画出了函数图象的一部分，请画出该函数图象的另一部分 .

(3)观察函数图象，写出两条函数的性质.

(4)进一步探究函数图象发现:

①方程-x2+2|x|+1=0有     个实数根;

②关于x的方程-x2+2|x|+1=a有4个实数根时，a的取值范围是           .

15.在函数学习中，我们经历“确定函数表法式-画数图象-利用函数图象研究函数性质一利用图象解决问题”的学习过程.画函数图象时，我们常通过描点或平移或翻折的方法画函数图象.请根据你学到的函数知识探究函数的图象与性质并利用图象解决如下问题:

列出y1与x的几组对应的值:

(1)根据表格中x、y1的对应关系可得m=        ; n=           .

(2)用你喜欢的方式画出该函数图象;根据函数图象;写出该函数的一条性质:               .

(3)直接写出当函数y1的图象与直线y2=kx+1有三个交点时，k的取值范围为                .