2020年湖北省十堰市中考数学试卷

这是一份2020年湖北省十堰市中考数学试卷，共19页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。


2020年湖北省十堰市中考数学试卷
题号
一
二
三
四
总分
得分






一、选择题（本大题共10小题，共30.0分）
1. 的倒数是（　　）
A. 4 B. -4 C. D. -
2. 某几何体的三视图如图所示，则此几何体是（　　）
A. 圆锥
B. 圆柱
C. 长方体
D. 四棱柱


3. 如图，将一副三角板重叠放在起，使直角顶点重合于点O．若∠AOC=130°，则∠BOD=（　　）
A. 30°
B. 40°
C. 50°
D. 60°


4. 下列计算正确的是（　　）
A. a+a2=a3 B. a6÷a3=a2
C. （-a2b）3=a6b3 D. （a-2）（a+2）=a2-4
5. 一家鞋店在一段时间内销售了某种女鞋30双，各种尺码鞋的销售量如下表所示：
鞋的尺码/cm
22
22.5
23
23.5
24
24.5
25
销售量双
1
2
5
11
7
3
1
若每双鞋的销售利润相同，则该店主最应关注的销售数据是下列统计量中的（　　）
A. 平均数 B. 方差 C. 众数 D. 中位数
6. 已知平行四边形ABCD中，下列条件：①AB=BC；②AC=BD；③AC⊥BD；④AC平分∠BAD，其中能说明平行四边形ABCD是矩形的是（　　）
A. ① B. ② C. ③ D. ④
7. 某厂计划加工180万个医用口罩，第一周按原计划的速度生产，一周后以原来速度的1.5倍生产，结果比原计划提前一周完成任务．若设原计划每周生产x万个口罩，则可列方程为（　　）
A. =+1 B. =-1
C. =+2 D. =-2
8. 如图，点A，B，C，D在⊙O上，OA⊥BC，垂足为E．若∠ADC=30°，AE=1，则BC=（　　）
A. 2
B. 4
C.
D. 2


9. 根据图中数字的规律，若第n个图中出现数字396，则n=（　　）


A. 17 B. 18 C. 19 D. 20
10. 如图，菱形ABCD的顶点分别在反比例函数y=和y=的图象上，若∠BAD=120°，则||=（　　）

A. B. 3 C. D.
二、填空题（本大题共6小题，共18.0分）
11. 已知x+2y=3，则1+2x+4y=______．
12. 如图，在△ABC中，DE是AC的垂直平分线．若AE=3，△ABD的周长为13，则△ABC的周长为______．


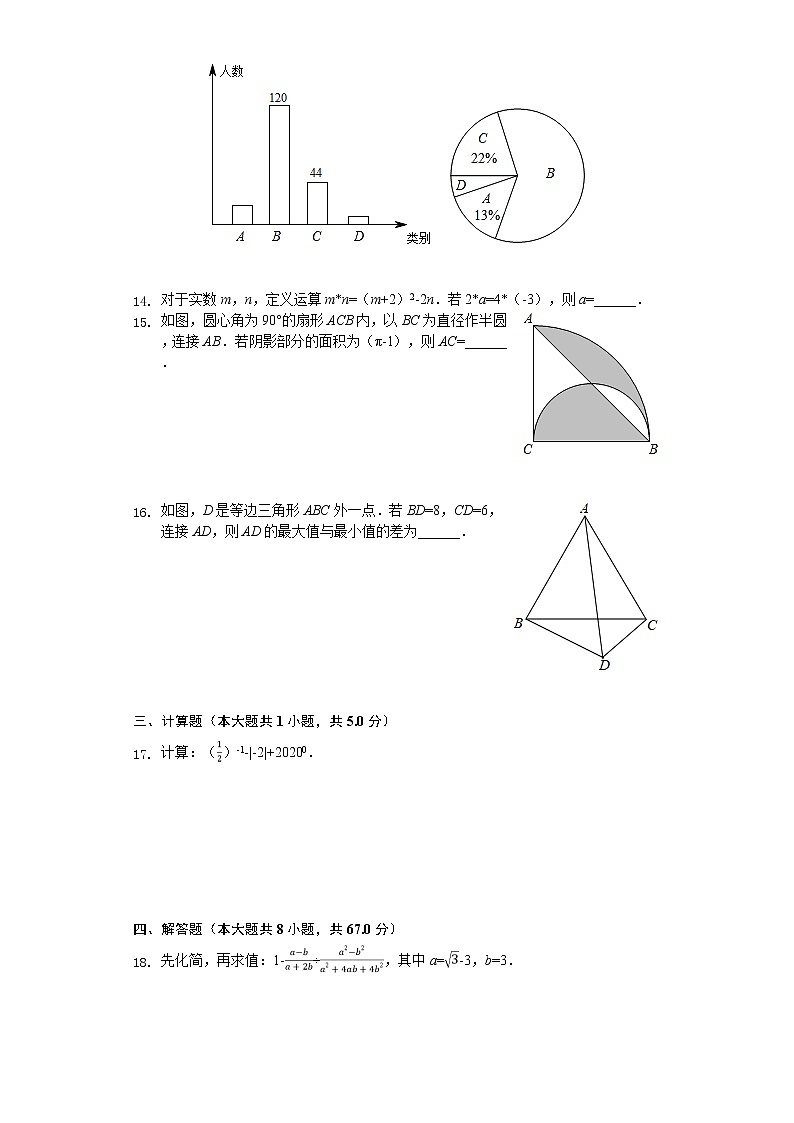
13. 某校即将举行30周年校庆，拟定了A，B，C，D四种活动方案，为了解学生对方案的意见，学校随机抽取了部分学生进行问卷调查（每人只能赞成一种方案），将调查结果进行统计并绘制成如图两幅不完整的统计图．若该校有学生3000人，请根据以上统计结果估计该校学生赞成方案B的人数为______．



14. 对于实数m，n，定义运算m*n=（m+2）2-2n．若2*a=4*（-3），则a=______．
15. 如图，圆心角为90°的扇形ACB内，以BC为直径作半圆，连接AB．若阴影部分的面积为（π-1），则AC=______．







16. 如图，D是等边三角形ABC外一点．若BD=8，CD=6，连接AD，则AD的最大值与最小值的差为______．









三、计算题（本大题共1小题，共5.0分）
17. 计算：（）-1-|-2|+20200．







四、解答题（本大题共8小题，共67.0分）
18. 先化简，再求值：1-÷，其中a=-3，b=3．







19. 如图，要想使人安全地攀上斜靠在墙面上的梯子的顶端，梯子与地面所成的角α一般要满足50°≤α≤75°，现有一架长为6m的梯子，当梯子底端离墙面2m时，此时人是否能够安全使用这架梯子（参考数据：sin50°≈0.77，cos50°≈0.64，sin75°≈0.97，cos75°=0.26）？









20. 某校开展“爱国主义教育”诵读活动，诵读读本有《红星照耀中国》、《红岩》、《长征》三种，小文和小明从中随机选取一种诵读，且他们选取每一种读本的可能性相同．
（1）小文诵读《长征》的概率是______；
（2）请用列表或画树状图的方法求出小文和小明诵读同一种读本的概率．







21. 已知关于x的一元二次方程x2-4x-2k+8=0有两个实数根x1，x2．
（1）求k的取值范围；
（2）若x13x2+x1x23=24，求k的值．







22. 如图，AB为半圆O的直径，C为半圆O上一点，AD与过点C的切线垂直，垂足为D，AD交半圆O于点E．
（1）求证：AC平分∠DAB；
（2）若AE=2DE，试判断以O，A，E，C为顶点的四边形的形状，并说明理由．







23. 某企业接到生产一批设备的订单，要求不超过12天完成．这种设备的出厂价为1200元/台，该企业第一天生产22台设备，第二天开始，每天比前一天多生产2台．若干天后，每台设备的生产成本将会增加，设第x天（x为整数）的生产成本为m（元/台），m与x的关系如图所示．
（1）若第x天可以生产这种设备y台，则y与x的函数关系式为______，x的取值范围为______；
（2）第几天时，该企业当天的销售利润最大？最大利润为多少？
（3）求当天销售利润低于10800元的天数．







24. 如图1，已知△ABC≌△EBD，∠ACB=∠EDB=90°，点D在AB上，连接CD并延长交AE于点F．
（1）猜想：线段AF与EF的数量关系为______；
（2）探究：若将图1的△EBD绕点B顺时针方向旋转，当∠CBE小于180°时，得到图2，连接CD并延长交AE于点F，则（1）中的结论是否还成立？若成立，请证明；若不成立，请说明理由；
（3）拓展：图1中，过点E作EG⊥CB，垂足为点G．当∠ABC的大小发生变化，其它条件不变时，若∠EBG=∠BAE，BC=6，直接写出AB的长．










25. 已知抛物线y=ax2-2ax+c过点A（-1，0）和C（0，3），与x轴交于另一点B，顶点为D．
（1）求抛物线的解析式，并写出D点的坐标；
（2）如图1，E为线段BC上方的抛物线上一点，EF⊥BC，垂足为F，EM⊥x轴，垂足为M，交BC于点G．当BG=CF时，求△EFG的面积；
（3）如图2，AC与BD的延长线交于点H，在x轴上方的抛物线上是否存在点P，使∠OPB=∠AHB？若存在，求出点P的坐标；若不存在，请说明理由．










答案和解析
1.【答案】A

【解析】解：的倒数是4
故选：A．
根据倒数的概念进行求解即可．
本题考查了倒数的概念，理解倒数的概念是解决本题的关键．
2.【答案】B

【解析】解：∵主视图和左视图都是长方形，
∴此几何体为柱体，
∵俯视图是一个圆，
∴此几何体为圆柱，
故选：B．
根据三视图的主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形进行分析可知几何体的名称．
此题考查了由三视图判断几何体，用到的知识点为：由主视图和左视图可得几何体是柱体，椎体还是球体，由俯视图可确定几何体的具体形状．
3.【答案】C

【解析】解：∵∠AOC=130°，
∴∠BOC=∠AOC-∠AOB=40°，
∴∠BOD=∠COD-∠BOC=50°．
故选：C．
根据角的和差关系求解即可．
本题考查角度的计算问题．弄清角与角之间的关系是解题的关键．
4.【答案】D

【解析】解：A、a与a2不是同类项，不能合并，原计算错误，故此选项不符合题意；
B、a6÷a3=a3，原计算错误，故此选项不符合题意；
C、（-a2b）3=-a6b3，原计算错误，故此选项不符合题意；
D、（a-2）（a+2）=a2-4，原计算正确，故此选项符合题意，
故选：D．
根据合并同类项法则、同底数幂的除法法则、积的乘方法则，平方差公式计算后，得出结果，作出判断．
此题主要考查了整式的运算，解题的关键是熟知公式和运算法则．
5.【答案】C

【解析】解：因为众数是在一组数据中出现次数最多的数，
又根据题意，每双鞋的销售利润相同，鞋店为销售额考虑，应关注卖出最多的鞋子的尺码，这样可以确定进货的数量，
所以该店主最应关注的销售数据是众数．
故选：C．
根据题意，联系商家最关注的应该是最畅销的鞋码，则考虑该店主最应关注的销售数据是众数．
本题主要考查数据的收集和处理．解题关键是熟悉统计数据的意义，并结合实际情况进行分析．根据众数是在一组数据中出现次数最多的数，再联系商家最关注的应该是最畅销的鞋码，则考虑该店主最应关注的销售数据是众数．
6.【答案】B

【解析】解：A．AB=BC，邻边相等的平行四边形是菱形，故A错误；
B．AC=BD，对角线相等的平行四边形是矩形，故B正确；
C．AC⊥BD，对角线互相垂直的平行四边形是菱形，故C错误；
D．AC平分∠BAD，对角线平分其每一组对角的平行四边形是菱形，故D错误．
故选：B．
根据矩形的判定进行分析即可．
本题考查了矩形的判定，熟知矩形从边，角，对角线三个方向的判定是解题的关键．
7.【答案】A

【解析】解：∵原计划每周生产x万个口罩，一周后以原来速度的1.5倍生产，
∴一周后每周生产1.5x万个口罩，
依题意，得：=+1．
故选：A．
由原计划每周生产的口罩只数结合一周后提高的速度，可得出一周后每周生产1.5x万个口罩，根据工作时间=工作总量÷工作效率结合实际比原计划提前一周完成任务（第一周按原工作效率），即可得出关于x的分式方程，此题得解．
本题考查了由实际问题抽象出分式方程，找准等量关系，正确列出分式方程是解题的关键．
8.【答案】D

【解析】解：连接OC，如图，
∵∠ADC=30°，
∴∠AOC=60°，
∵OA⊥BC，
∴CE=BE，
在Rt△COE中，OE=OC，CE=OE，
∵OE=OA-AE=OC-1，
∴OC-1=OC，
∴OC=2，
∴OE=1，
∴CE=，
∴BC=2CE=2．
故选：D．
连接OC，根据圆周角定理求得∠AOC=60°，在Rt△COE中可得OE=OC=OC-1得到OC=2，从而得到CE=，然后根据垂径定理得到BC的长．
本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了垂径定理．
9.【答案】B

【解析】解：根据图形规律可得：
上三角形的数据的规律为：2n（1+n），若2n（1+n）=396，解得n不为正整数，舍去；
下左三角形的数据的规律为：n2-1，若n2-1=396，解得n不为正整数，舍去；
下中三角形的数据的规律为：2n-1，若2n-1=396，解得n不为正整数，舍去；
下右三角形的数据的规律为：n（n+4），若n（n+4）=396，解得n=18，或n=-22，舍去
故选：B．
观察上三角形，下左三角形，下中三角形，下右三角形各自的规律，让其等于396，解得n为正整数即成立，否则舍去．
本题考查了图形有关数字的规律，能准确观察到相关规律是解题的关键
10.【答案】B

【解析】解：根据对称性可知，反比例函数，的图象是中心对称图形，菱形是中心对称图形，
∴菱形ABCD的对角线AC与BD的交点即为原点O，OD⊥OC，
如图：作CM⊥x轴于M，DN⊥x轴于N．连接OD，OC．
∵DO⊥OC，
∴∠COM+∠DON=90°，∠DON+∠ODN=90°，
∴∠COM=∠ODN，
∵∠CMO=∠DNO=90°，
∴△COM∽△ODN，
∴，
∵菱形ABCD的对角线AC与BD的交点即为原点O，∠BAD=120°，
∴∠OCD=60°，∠COD=90°，
∴，
∴，
∴，
∴．
故选：B．
据对称性可知，反比例函数，的图象是中心对称图形，菱形是中心对称图形，推出菱形ABCD的对角线AC与BD的交点即为原点O．如图：作CM⊥x轴于M，DN⊥x轴于N．连接OD，OC．证明△COM∽△ODN，利用相似三角形的性质可得答案．
本题考查菱形的性质、反比例函数的图象与性质、相似三角形的判定与性质，锐角三角函数等知识，解题的关键是灵活运用所学知识解决问题．
11.【答案】7

【解析】解：∵x+2y=3，
∴2（x+2y）=2x+4y=2×3=6，
∴1+2x+4y=1+6=7，
故答案为：7．
由x+2y=3可得到2x+4y=6，然后整体代入1+2x+4y计算即可．
本题考查了代数式的求值问题，注意整体代入的思想是解题的关键．
12.【答案】19

【解析】解：∵DE是AC的垂直平分线，AE=3，
∴AC=2AE=6，AD=DC，
∵AB+BD+AD=13，
∴△ABC的周长=AB+BC+AC=AB+BD+AD+AC=13+6=19．
故答案为：19．
由线段的垂直平分线的性质可得AC=2AE，AD=DC，从而可得答案．
本题考查的是线段的垂直平分线的性质，掌握线段的垂直平分线的性质是解题的关键．
13.【答案】1800人

【解析】解：根据条形统计图和扇形统计图可知赞成C方案的有44人，占样本的22%，
∴样本容量为：44÷22%=200（人），
∴赞成方案B的人数占比为：，
∴该校学生赞成方案B的人数为：3000×60%=1800（人），
故答案为：1800人．
根据条形统计图和扇形统计图可知赞成C方案的有44人，占样本的22%，可得出样本容量，即可得到赞成方案B的人数占比，用样本估计总体即可求解．
本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．
14.【答案】-13

【解析】解：∵m*n=（m+2）2-2n，
∴2*a=（2+2）2-2a=16-2a，4*（-3）=（4+2）2-2×（-3）=42，
∵2*a=4*（-3），
∴16-2a=42，
解得a=-13，
故答案为：-13．
根据给出的新定义分别求出2*a与4*（-3）的值，根据2*a=4*（-3）得出关于a的一元一次方程，求解即可．
本题考查解一元一次方程、新定义下实数的运算等内容，理解题干中给出的新定义是解题的关键．
15.【答案】2

【解析】解：将原图区域划分为四部分，阴影部分分别为S1，S2；两块空白分别为S3，S4，连接DC，如下图所示：
由已知得：三角形ABC为等腰直角三角形，S1+S2=π-1，
∵BC为直径，
∴∠CDB=90°，即CD⊥AB，
故CD=DB=DA，
∴D点为中点，由对称性可知与弦CD围成的面积与S3相等．
设AC=BC=x，
则S扇ACB-S3-S4=S1+S2，
其中，
，
故：，
求解得：x1=2，x2=-2（舍去）
故答案：2．

本题可利用扇形面积公式以及三角形面积公式，用大扇形面积减去空白部分面积求得阴影部分面积，继而根据已知列方程求解．
本题考查几何图形面积的求法，常用割补法配合扇形面积公式以及三角形面积公式求解．
16.【答案】12

【解析】解：如图，以CD为边向外作等边△CDE，连接BE，

∵△CDE和△ABC是等边三角形，
∴CE=CD，CB=CA，∠ECD=∠BCA=60°，
∴∠ECB=∠DCA，
在△ECB和△DCA中，，
∴△ECB≌△DCA（SAS），
∴BE=AD，
∵DE=CD=6，BD=8，
∴在△BDE中，BD-DE＜BE＜BD+DE，
即8-6＜BE＜8+6，
∴2＜BE＜14，
∴2＜AD＜14．
∴则AD的最大值与最小值的差为14-2=12．
故答案为：12．
以CD为边向外作等边△CDE，连接BE，可证得△ECB≌△DCA从而得到BE=AD，再根据三角形的三边关系即可得出结论．
本题考查了全等三角形的判定与性质、等边三角形的性质以及三角形的三边关系，解题关键在于添加辅助线构建全等三角形把AD转化为BE从而求解，是一道较好的中考题．
17.【答案】解：
=2-2+1
=1．

【解析】根据负整数指数幂，绝对值的运算，0次幂分别计算出每一项，再计算即可．
本题考查负整数指数幂，绝对值的运算，0次幂等知识点，熟练掌握运算法则是解题的关键．
18.【答案】解：原式=1-÷
=1-•
=1-
=
=-，
当a=-3，b=3时，原式=-=-．

【解析】利用完全平方公式、平方差公式和通分等方法将原分式化简成-，再将a、b的值代入化简后的分式中即可得出结论．
本题考查分式的化简求值，掌握分式的运算法则是解题的关键．
19.【答案】解：在Rt△ABC中，
∵cosα=，
∴AC=AB•cosα，
当α=50°时，AC=AB•cosα≈6×0.64≈3.84m；
当α=75°时，AC=AB•cosα≈6×0.26≈1.56m；
所以要想使人安全地攀上斜靠在墙面上的梯子的顶端，梯子底端与墙面的距离应该在1.56m～3.84m之间，
故当梯子底端离墙面2m时，此时人能够安全使用这架梯子．

【解析】分别求出当α=50°时和当α=75°时梯子底端与墙面的距离AC的长度，再进行判断即可．
本题考查解直角三角形的应用，求出人能够安全使用这架梯子时，梯子底端与墙面的安全距离的范围是解题的关键．
20.【答案】

【解析】解：（1）P（小文诵读《长征》）=；
故答案为：；

（2）记《红星照耀中国》、《红岩》、《长征》分别为A、B、C，
列表如下：

A
B
C
A
（A，A）
（A，B）
（A，C）
B
（B，A）
（B，B）
（B，C）
C
（C，A）
（C，B）
（C，C）
由表格可知，共有9种等可能性结果，其中小文和小明诵读同一种读本的有3种结果，
∴小文和小明诵读同一种读本的概率为．
（1）根据概率公式即可求解；
（2）根据题意画出树状图，利用概率公式即可求解．
本题考查了用列表法或画树形图法求随机事件的概率，用到的知识点为：概率=所求情况数与总情况数之比；得到所求的情况数是解决本题的关键．
21.【答案】解：（1）由题意可知，△=（-4）2-4×1×（-2k+8）≥0，
整理得：16+8k-32≥0，
解得：k≥2，
∴k的取值范围是：k≥2．
故答案为：k≥2．
（2）由题意得：，
由韦达定理可知：x1+x2=4，x1x2=-2k+8，
故有：（-2k+8）[42-2（-2k+8）]=24，
整理得：k2-4k+3=0，
解得：k1=3，k2=1，
又由（1）中可知k≥2，
∴k的值为k=3．
故答案为：k=3．

【解析】（1）根据△≥0建立不等式即可求解；
（2）先提取公因式对等式变形为，再结合韦达定理求解即可．
本题考查了一元二次方程根的判别式、根与系数的关系、韦达定理、一元二次方程的解法等知识点，当△＞0时，方程有两个不相等的实数根；当△=0时，方程有两个相等的实数根；当△＜0时，方程没有实数根．
22.【答案】解：（1）证明：连接OC，如下图所示：
∵CD为圆O的切线，∴∠OCD=90°，
∴∠D+∠OCD=180°，
∴OC∥AD，
∴∠DAC=∠ACO，
又OC=OA，
∴∠ACO=∠OAC，
∴∠DAC=∠OAC，
∴AC平分∠DAB．
（2）四边形EAOC为菱形，理由如下：
连接EC、BC、EO，过C点作CH⊥AB于H点，如下图所示，
由圆内接四边形对角互补可知，∠B+∠AEC=180°，
又∠AEC+∠DEC=180°，
∴∠DEC=∠B，
又∠B+∠CAB=90°，
∠DEC+∠DCE=90°，
∴∠CAB=∠DCE，
又∠CAB=∠CAE，
∴∠DCE=∠CAE，且∠D=∠D，
∴△DCE∽△DAC，
设DE=x，则AE=2x，AD=AE+DE=3x，
∴，∴CD2=AD•DE=3x2，
∴，
在Rt△ACD中，，
∴∠DAC=30°，
∴∠DAO=2∠DAC=60°，且OA=OE，
∴△OAE为等边三角形，
由同弧所对的圆周角等于圆心角的一半可知：∠EOC=2∠EAC=60°，
∴△EOC为等边三角形，
∴EA=AO=OE=EC=CO，
即EA=AO=OC=CE，
∴四边形EAOC为菱形．

【解析】（1）连接OC，由切线的性质可知∠OCD+∠D=180°，进而得到OC∥AD，得到∠DAC=∠ACO，再由OC=OA得到∠ACO=∠OAC，进而得到∠DAC=∠OAC即可证明；
（2）连接EC、BC、EO，过C点作CH⊥AB于H点，先证明∠DCE=∠CAE，进而得到△DCE∽△DAC，再由AE=2DE结合三角函数求出∠EAC=30°，最后证明△EAO和△ECO均为等边三角形即可求解．
本题考查了圆周角定理、相似三角形的判定和性质、三角函数、菱形的判定等知识点，属于综合题，熟练掌握其性质和定理是解决本题的关键．
23.【答案】y=2x+20  1≤x≤12

【解析】解：（1）根据题意，得y与x的解析式为：y=22+2（x-1）=2x+20（1≤x≤12），
故答案为：y=2x+20，1≤x≤12；
（2）设当天的销售利润为w元，
则当1≤x≤6时，
w=（1200-800）（2x+20）=800x+8000，
∵800＞0，
∴w随x的增大而增大，
∴当x=6时，w最大值=800×6+8000=12800．
当6＜x≤12时，
设m=kx+b，将（6，800）和（10，1000）代入得：
，
解得：，
∴m与x的关系式为：m=50x+500，
∴w=[1200-（50x+500）]×（2x+20）
=-100x2+400x+14000
=-100（x-2）2+14400．
∵此时图象开口向下，在对称轴右侧，w随x的增大而减小，天数x为整数，
∴当x=7时，w有最大值，为11900元，
∵12800＞11900，
∴当x=6时，w最大，且w最大值=12800元，
答：该厂第6天获得的利润最大，最大利润是12800元．
（3）由（2）可得，
1≤x≤6时，800x+8000＜10800，
解得：x＜3.5
则第1-3天当天利润低于10800元，
当6＜x≤12时，-100（x-2）2+14400＜10800，
解得x＜-4（舍去），或x＞8，
∴第9-12天当天利润低于10800元，
故当天销售利润低于10800元的天数有7天．
（1）根据题意确定一次函数的解析式，实际问题中x的取值范围要使实际问题有意义；
（2）求出当天利润与天数的函数解析式，确定其最大值即可；
（3）根据（2）中的函数解析式列出不等式方程即可解答．
本题主要考查了一次函数和二次函数的应用，解题的关键在于理解题意、利用待定系数法确定函数的解析式并分类讨论．
24.【答案】AF=EF

【解析】解：（1）延长DF到K点，并使FK=DC，连接KE，如图1所示，
∵△ABC≌△EBD，
∴DE=AC，BD=BC，
∴∠CDB=∠DCB，且∠CDB=∠ADF，
∴∠ADF=∠DCB，
∵∠ACB=90°，
∴∠ACD+∠DCB=90°，
∵∠EDB=90°，
∴∠ADF+∠FDE=90°，
∴∠ACD=∠FDE，
∵FK+DF=DC+DF，
∴DK=CF，
在△ACF和△EDK中，，
∴△ACF≌△EDK（SAS），
∴KE=AF，∠K=∠AFC，
又∠AFC=∠KFE，
∴∠K=∠KFE
∴KE=EF
∴AF=EF，
故AF与EF的数量关系为：AF=EF．
故答案为：AF=EF；

（2）仍旧成立，理由如下：
延长DF到K点，并使FK=DC，连接KE，如图2所示，
设BD延长线DM交AE于M点，
∵△ABC≌△EBD，
∴DE=AC，BD=BC，
∴∠CDB=∠DCB，且∠CDB=∠MDF，
∴∠MDF=∠DCB，
∵∠ACB=90°，
∴∠ACD+∠DCB=90°，
∵∠EDB=90°，
∴∠MDF+∠FDE=90°，
∴∠ACD=∠FDE，
∵FK+DF=DC+DF，
∴DK=CF，
在△ACF和△EDK中，，
∴△ACF≌△EDK（SAS），
∴KE=AF，∠K=∠AFC，
又∠AFC=∠KFE，
∴∠K=∠KFE，
∴KE=EF，
∴AF=EF，
故AF与EF的数量关系为：AF=EF．

（3）如图3所示，延长DF到K点，并使FK=DC，连接KE，过点E作EG⊥BC交CB的延长线于G，
∵BA=BE，
∴∠BAE=∠BEA，
∵∠BAE=∠EBG，
∴∠BEA=∠EBG，
∴AE∥CG，
∴∠AEG+∠G=180°，
∴∠AEG=90°，
∴∠ACG=∠G=∠AEG=90°，
∴四边形AEGC为矩形，
∴AC=EG，且AB=BE，
∴Rt△ACB≌Rt△EGB（HL），
∴BG=BC=6，∠ABC=∠EBG，
又∵ED=AC=EG，且EB=EB，
∴Rt△EDB≌Rt△EGB（HL），
∴DB=GB=6，∠EBG=∠ABE，
∴∠ABC=∠ABE=∠EBG=60°，
∴∠BAC=30°，
∴在Rt△ABC中，由30°所对的直角边等于斜边的一半可知：AB=2BC=12．
（1）延长DF到K点，并使FK=DC，连接KE，证明△ACF≌△EDK，进而得到△KEF为等腰三角形，即可证明AF=KE=EF；
（2）证明原理同（1），延长DF到K点，并使FK=DC，连接KE，证明△ACF≌△EDK，进而得到△KEF为等腰三角形，即可证明AF=KE=EF；
（3）补充完整图后证明四边形AEGC为矩形，进而得到∠ABC=∠ABE=∠EBG=60°即可求解．
本题属于几何变换综合题，考查了三角形全等的性质和判定，矩形的性质和判定，本题的关键是延长DF到K点并使FK=DC，进而构造全等三角形．
25.【答案】（1）把点A（-1，0），C（0，3）代入y=ax2-2ax+c中，，
解得，
∴y=-x2+2x+3，
当时，y=4，
∴D（1，4）；

（2）如图1，∵抛物线y=-x2+2x+3，
令y=0，
∴x=-1，或x=3，
∴B（3，0）．
设BC的解析式为y=kx+b（k≠0），
将点C（0，3），B（3，0）代入，得，
解得，
∴y=-x+3．
∵EF⊥CB．
设直线EF的解析式为y=x+b，设点E的坐标为（m，-m2+2m+3），
将点E坐标代入y=x+b中，得b=-m2+m+3，
∴y=x-m2+m+3．
∴．
∴．
把x=m代入y=-x+3，得y=-m+3，
∴G（m，-m+3）．
∵BG=CF．
∴BG2=CF2，即．
解得m=2或m=-3．
∵点E是BC上方抛物线上的点，
∴m=-3，舍去．
∴点E（2，3），F（1，2），G（2，1），，
∴；

（3）如图2，过点A作AN⊥HB，
∵点D（1，4），B（3，0），
∴yDB=-2x+6．
∵点A（-1，0），点C（0，3），
∴yAC=3x+3，
∴，
∴．
设，把（-1，0）代入，得b=，
∴，
∴，
∴，
∴=，
∴AN=HN．
∴∠H=45°．
设点p（n，-n2+2n+3）．
过点P作PR⊥x轴于点R，在x轴上作点S使得RS=PR，
∴∠RSP=45°且点S的坐标为（-n2+3n+3，0）．
若∠OPB=∠AHB=45°
在△OPS和△OPB中，∠POS=∠POB，∠OSP=∠OPB，
∴△OPS∽△OPB．
∴．
∴OP2=OB•OS．
∴n2+（n+1）2（n-3）2=3•（-n2+2n+3）．
∴n=0或．
∴P1（0，3），，．

【解析】（1）利用待定系数法求出a的值即可得到解析式，进而得到顶点D坐标；
（2）先求出BC的解析式y=-x+3，再设直线EF的解析式为y=x+b，设点E的坐标为（m，-m2+2m+3），联立方程求出点F，G的坐标，根据BG2=CF2列出关于m的方程并求解，然后求得G的坐标，再利用三角形面积公式求解即可；
（3）过点A作AN⊥HB，先求得直线BD，AN的解析式，得到H，N的坐标，进而得到∠H=45°，设点p（n，-n2+2n+3），过点P作PRx轴于点R，在x轴上作点S使得RS=PR，证明△OPS∽△OPB，根据相似三角形对应边成比例得到关于n的方程，求得后即可得到点P的坐标．
本题考查的是二次函数的综合，涉及到的知识点较多，运算较复杂，第3问的解题关键在于添加适当的辅助线，利用数形结合的思想列出方程求解．