

- 2021届高三文科数学《大题精练》 (2) 试卷 3 次下载
- 2021届高三文科数学《大题精练》 (3) 试卷 2 次下载
- 2021届高三文科数学《大题精练》 (5) 试卷 2 次下载
- 2021届高三文科数学《大题精练》 (6) 试卷 2 次下载
- 2021届高三文科数学《大题精练》 (7) 试卷 2 次下载
2021届高三文科数学《大题精练》 (4)
展开2021届高三数学(文)“大题精练”4
17.(本小题满分12分)
已知等差数列中,为其前项和,;等比数列的前项和
(I)求数列的通项公式;
(II)当各项为正时,设,求数列的前项和.
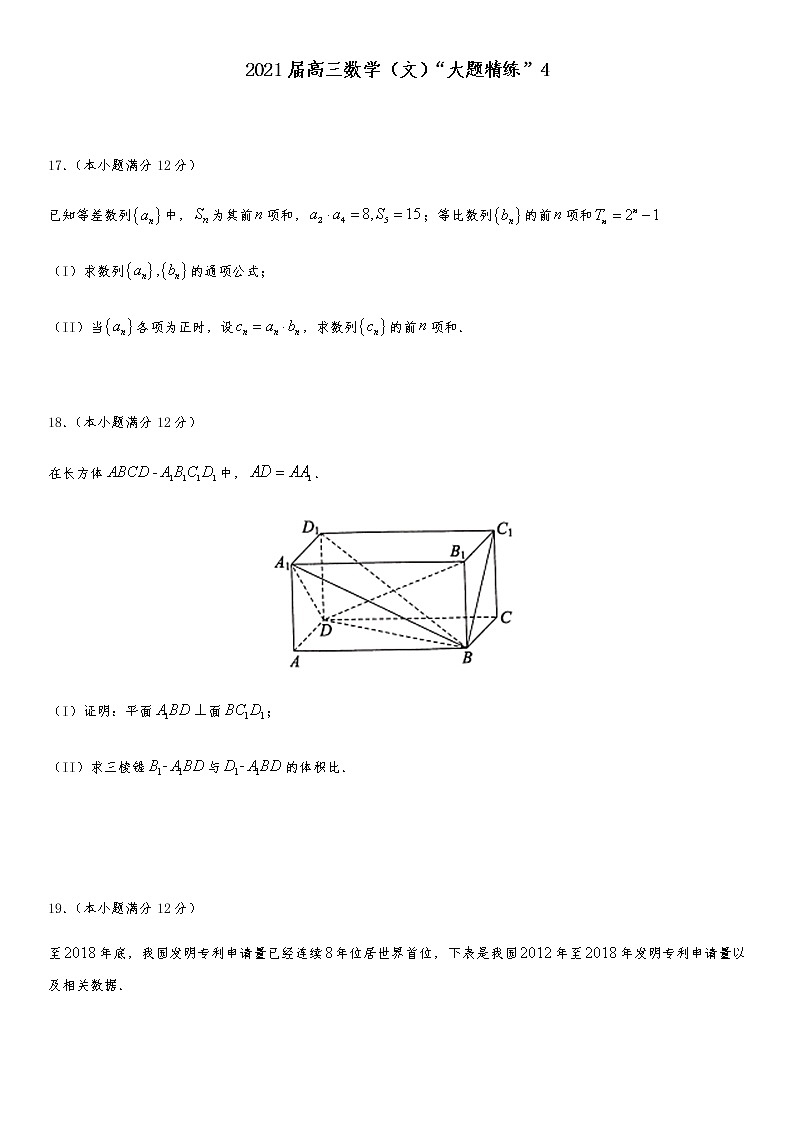
18.(本小题满分12分)
在长方体中,.
(I)证明:平面面;
(II)求三棱锥与的体积比.
19.(本小题满分12分)
至年底,我国发明专利申请量已经连续年位居世界首位,下表是我国年至年发明专利申请量以及相关数据.
注:年份代码~分别表示~.
(I)可以看出申请量每年都在增加,请问这几年中哪一年的增长率达到最高,最高是多少?
(II)建立关于的回归直线方程(精确到),并预测我国发明专利申请量突破万件的年份.
参考公式:回归直线的斜率和截距的最小二乘法估计分别为,
20.(本小题满分12分)
已知抛物线的焦点为,若过且倾斜角为的直线交于,两点,满足.
(I)求抛物线的方程;
(II)若为上动点,,在轴上,圆内切于,求面积的最小值.
21.(本小题满分12分)
已知函数.
(I)求函数在上的最大值;
(II)若函数有两个零点,证明:.
请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分.
22.选修4-4:坐标系与参数方程(本小题满分10分)
在直角坐标系中,曲线的参数方程为为参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系.
(I)求曲线的极坐标方程;
(II)设为曲线上不同两点(均不与重合),且满足,求的最大面积.
23.选修4-5:不等式选讲(本小题满分10分)
设函数
(I)解不等式;
(II)当,时,证明:.
2020届高三数学(文)“大题精练”4(答案解析)
17.(本小题满分12分)
已知等差数列中,为其前项和,;等比数列的前项和
(I)求数列的通项公式;
(II)当各项为正时,设,求数列的前项和.
【解析】(I)设等差数列的首项为,公差为,
则,
,,
当时,;当时,也满足上式,∴.
(II)由题可知,,
,
,
,故.
18.(本小题满分12分)
在长方体中,.
(I)证明:平面面;
(II)求三棱锥与的体积比.
【解析】(I)证明:连接,∵,∴四边形是正方形,∴,
由题,∵,∴,
又,,平面,∴平面,
又平面,∴平面平面.
(II)解:连结,由题,∵,∴平面,∴,到平面的距离相等,
故三棱锥与的体积比为1:1.
19.(本小题满分12分)
至年底,我国发明专利申请量已经连续年位居世界首位,下表是我国年至年发明专利申请量以及相关数据.
注:年份代码~分别表示~.
(I)可以看出申请量每年都在增加,请问这几年中哪一年的增长率达到最高,最高是多少?
(II)建立关于的回归直线方程(精确到),并预测我国发明专利申请量突破万件的年份.
参考公式:回归直线的斜率和截距的最小二乘法估计分别为,
【解析】(I)由表格可知2013,2014,2015,2016,2017,2018年的增长率分别如下:,
∴2013年的增长率最高,达到了26%.
(II)由表格可计算出:,,关于的回归直线方程为.
令,
∴根据回归方程可预测,我国发明专利申请量将在2021年突破200万件.
20.(本小题满分12分)
已知抛物线的焦点为,若过且倾斜角为的直线交于,两点,满足.
(I)求抛物线的方程;
(II)若为上动点,,在轴上,圆内切于,求面积的最小值.
【解析】(I)抛物线的焦点为,则过点且斜率为1的直线方程为,
联立抛物线方程,消去得:,
设,则,
由抛物线的定义可得,解得,∴抛物线的方程为.
(II)设,,,不妨设,,化简得:,
圆心到直线的距离为1,故,
即,不难发现,
上式又可化为,同理有,
∴可以看做关于的一元二次方程的两个实数根,
,,
由条件:,
,当且仅当时取等号,
∴面积的最小值为8.
21.(本小题满分12分)
已知函数.
(I)求函数在上的最大值;
(II)若函数有两个零点,证明:.
【解析】(I)∵,则.
令,解得.
当时,;
当时,,
故函数的增区间为,减区间为.
当,即时,在区间上单调连增,则;
当,即时,在区间上单调递墙,在区间上单调递减,则;
当,即时,在区间上单调递减,则.
(II)证明:若函数有两个零点,则,可得.
则,此时,由此可得,故,即.
又∵,∴,则.
请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分.
22.选修4-4:坐标系与参数方程(本小题满分10分)
在直角坐标系中,曲线的参数方程为为参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系.
(I)求曲线的极坐标方程;
(II)设为曲线上不同两点(均不与重合),且满足,求的最大面积.
【解析】(I)设曲线上任意点的极坐标为,由题意,曲线的普通方程为,即,则,故曲线的极坐标方程为.
(II)设,则,故,
∵点在曲线上,则,,
,
故时,取到最大面积为.
23.选修4-5:不等式选讲(本小题满分10分)
设函数
(I)解不等式;
(II)当,时,证明:.
【解析】(I)由已知可得:,
当时,成立;
当时,,即,则.
∴的解集为.
(II)由(I)知,,
由于,则,当且仅当,即时取等号,则有.
2021届高三文科数学《大题精练》 (5): 这是一份2021届高三文科数学《大题精练》 (5),共12页。试卷主要包含了选修4-4,选修4-5,024,635等内容,欢迎下载使用。
2021届高三文科数学《大题精练》 (9): 这是一份2021届高三文科数学《大题精练》 (9),共11页。试卷主要包含了已知函数,.等内容,欢迎下载使用。
2021届高三文科数学《大题精练》 (13): 这是一份2021届高三文科数学《大题精练》 (13),共13页。试卷主要包含了已知数列的前项和为,.,646,82亿吨等内容,欢迎下载使用。












