2020年湖南省邵阳市中考数学试卷

这是一份2020年湖南省邵阳市中考数学试卷，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2020年湖南省邵阳市中考数学试卷
题号
一
二
三
总分
得分





一、选择题（本大题共10小题，共30.0分）
1. 2020的倒数是（　　）
A. -2020 B. 2020 C. D. -
2. 下列四个立体图形中，它们各自的三视图都相同的是（　　）
A. B. C. D.
3. 2020年6月23日，中国第55颗北斗导航卫星成功发射，标志着拥有全部知识产权的北斗导航系统全面建成．据统计：2019年，我国北斗卫星导航与位置服务产业总体产值达3450亿元，较2018年增长14.4%．其中，3450亿元用科学记数法表示为（　　）
A. 3.45×1010元 B. 3.45×109元 C. 3.45×108元 D. 3.45×1011元
4. 设方程x2-3x+2=0的两根分别是x1，x2，则x1+x2的值为（　　）
A. 3 B. - C. D. -2
5. 已知正比例函数y=kx（k≠0）的图象过点（2，3），把正比例函数y=kx（k≠0）的图象平移，使它过点（1，-1），则平移后的函数图象大致是（　　）
A. B.
C. D.
6. 下列计算正确的是（　　）
A. 5+=8 B. （-2a2b）3=-6a2b3
C. （a-b）2=a2-b2 D. =a-2
7. 如图，四边形ABCD是平行四边形，点E，B，D，F在同一条直线上，请添加一个条件使得△ABE≌△CDF，下列不正确的是（　　）

A. AE=CF B. ∠AEB=∠CFD C. ∠EAB=∠FCD D. BE=DF
8. 已知a+b＞0，ab＞0，则在如图所示的平面直角坐标系中，小手盖住的点的坐标可能是（　　）
A. （a，b）
B. （-a，b）
C. （-a，-b）
D. （a，-b）


9. 如图①所示，平整的地面上有一个不规则图案（图中阴影部分），小明想了解该图案的面积是多少，他采取了以下办法：用一个长为5m，宽为4m的长方形，将不规则图案围起来，然后在适当位置随机地朝长方形区域扔小球，并记录小球落在不规则图案上的次数（球扔在界线上或长方形区域外不计实验结果），他将若干次有效实验的结果绘制成了②所示的折线统计图，由此他估计不规则图案的面积大约为（　　）


A. 6m2 B. 7m2 C. 8m2 D. 9m2
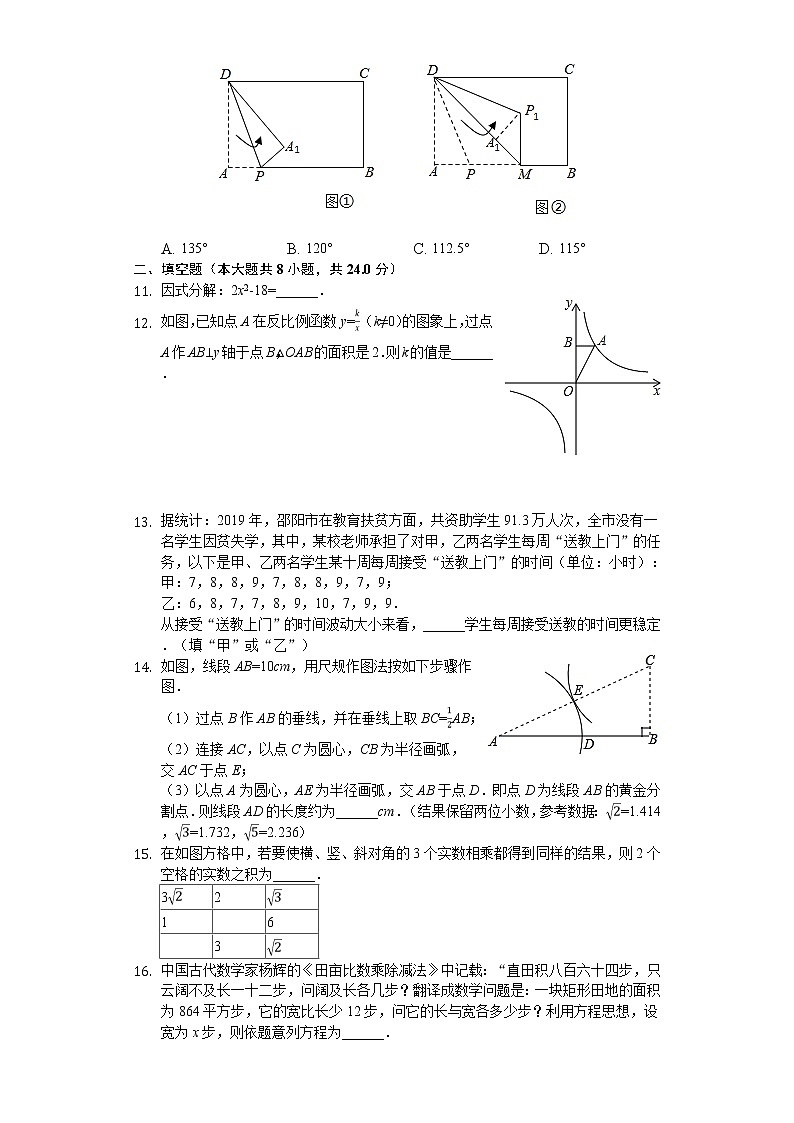
10. 将一张矩形纸片ABCD按如图所示操作：
（1）将DA沿DP向内折叠，使点A落在点A1处，
（2）将DP沿DA1向内继续折叠，使点P落在点P1处，折痕与边AB交于点M．
若P1M⊥AB，则∠DP1M的大小是（　　）


A. 135° B. 120° C. 112.5° D. 115°
二、填空题（本大题共8小题，共24.0分）
11. 因式分解：2x2-18=______．
12. 如图，已知点A在反比例函数y=（k≠0）的图象上，过点A作AB⊥y轴于点B，△OAB的面积是2．则k的值是______．







13. 据统计：2019年，邵阳市在教育扶贫方面，共资助学生91.3万人次，全市没有一名学生因贫失学，其中，某校老师承担了对甲，乙两名学生每周“送教上门”的任务，以下是甲、乙两名学生某十周每周接受“送教上门”的时间（单位：小时）：
甲：7，8，8，9，7，8，8，9，7，9；
乙：6，8，7，7，8，9，10，7，9，9．
从接受“送教上门”的时间波动大小来看，______学生每周接受送教的时间更稳定．（填“甲”或“乙”）
14. 如图，线段AB=10cm，用尺规作图法按如下步骤作图．
（1）过点B作AB的垂线，并在垂线上取BC=AB；
（2）连接AC，以点C为圆心，CB为半径画弧，交AC于点E；
（3）以点A为圆心，AE为半径画弧，交AB于点D．即点D为线段AB的黄金分割点．则线段AD的长度约为______cm．（结果保留两位小数，参考数据：=1.414，=1.732，=2.236）
15. 在如图方格中，若要使横、竖、斜对角的3个实数相乘都得到同样的结果，则2个空格的实数之积为______．
3
2

1

6

3

16. 中国古代数学家杨辉的《田亩比数乘除减法》中记载：“直田积八百六十四步，只云阔不及长一十二步，问阔及长各几步？翻译成数学问题是：一块矩形田地的面积为864平方步，它的宽比长少12步，问它的长与宽各多少步？利用方程思想，设宽为x步，则依题意列方程为______．
17. 如图①是山东舰航徽的构图，采用航母45度破浪而出的角度，展现山东舰作为中国首艘国产舰母橫空出世的气势，将舰徽中第一条波浪抽象成几何图形，则是一条长为10π的弧，若该弧所在的扇形是高为12的圆锥侧面展开图（如图②），则该圆锥的母线长AB为______．



18. 如图，在Rt△ABC中，∠ACB=90°，斜边AB=，过点C作CF∥AB，以AB为边作菱形ABEF，若∠F=30°，则Rt△ABC的面积为______．


三、解答题（本大题共8小题，共66.0分）
19. 计算：（-1）2020+（）-1+|-1+|-2sin60°．







20. 已知：|m-1|+=0，
（1）求m，n的值；
（2）先化简，再求值：m（m-3n）+（m+2n）2-4n2．







21. 如图，在等腰△ABC中，AB=AC，点D是BC上一点，以BD为直径的⊙O过点A，连接AD，∠CAD=∠C．
（1）求证：AC是⊙O的切线；
（2）若AC=4，求⊙O的半径．












22. 2019年12月23日，湖南省政府批准，全国“十三五”规划重大水利工程--邵阳资水犬木塘水库，将于2020年开工建设施工测绘中，饮水干渠需经过一座险峻的石山，如图所示，AB，BC表示需铺设的干渠引水管道，经测量，A，B，C所处位置的海拔AA1，BB1，CC1分别为62m，100m，200m．若管道AB与水平线AA2的夹角为30°，管道BC与水平线BB2夹角为45°，求管道AB和BC的总长度（结果保留根号）．









23. “新冠病毒”疫情防控期间，我市积极开展“停课不停学”网络教学活动，为了了解和指导学生有效进行网络学习，某校对学生每天在家网络学习时间进行了随机问卷调查（问卷调查表如图所示），并用调查结果绘制了图①，图②两幅统计图（均不完整），请根据统计图解答以下问题：

xx学校“停课不停学”网络学习时间
调查表
亲爱的同学，你好！
为了了解和更好地指导你进行“停课不停学”网络学习，请在表格中选择一项符合你学习时间的选项，在其后的空格内打“√”．
平均每天利用网络学习时间问卷调查表
选项
学习时间（小时）

A
0＜t≤1

B
1＜t≤3

C
3＜t≤5

D
t＞5


（1）本次接受问卷调查的学生共有______人；
（2）请补全图①中的条形统计图；
（3）图②中，D选项所对应的扇形圆心角为______度；
（4）若该校共有1500名学生，请你估计该校学生“停课不停学”期间平均每天利用网络学习时间在C选项的有多少人？







24. 2020年5月，全国“两会”召开以后，应势复苏的“地摊经济”带来了市场新活力，小丹准备购进A、B两种类型的便携式风扇到地摊一条街出售．已知2台A型风扇和5台B型风扇进价共100元，3台A型风扇和2台B型风扇进价共62元．
（1）求A型风扇、B型风扇进货的单价各是多少元？
（2）小丹准备购进这两种风扇共100台，根据市场调查发现，A型风扇销售情况比B型风扇好，小丹准备多购进A型风扇，但数量不超过B型风扇数量的3倍，购进A、B两种风扇的总金额不超过1170元．根据以上信息，小丹共有哪些进货方案？







25. 已知：如图①，将一块45°角的直角三角板DEF与正方形ABCD的一角重合，连接AF，CE，点M是CE的中点，连接DM．
（1）请你猜想AF与DM的数量关系是______．
（2）如图②，把正方形ABCD绕着点D顺时针旋转α角（0°＜α＜90°）．
①AF与DM的数量关系是否仍成立，若成立，请证明；若不成立，请说明理由；（温馨提示：延长DM到点N，使MN=DM，连接CN）
②求证：AF⊥DM；
③若旋转角α=45°，且∠EDM=2∠MDC，求的值．（可不写过程，直接写出结果）









26. 如图，在平面直角坐标系中，矩形ABCD的边BC与x轴、y轴的交点分别为C（8，0），B（0，6），CD=5，抛物线y=ax2-x+c（a≠0）过B，C两点，动点M从点D开始以每秒5个单位长度的速度沿D→A→B→C的方向运动到达C点后停止运动．动点N从点O以每秒4个单位长度的速度沿OC方向运动，到达C点后，立即返回，向CO方向运动，到达O点后，又立即返回，依此在线段OC上反复运动，当点M停止运动时，点N也停止运动，设运动时间为t．
（1）求抛物线的解析式；
（2）求点D的坐标；
（3）当点M，N同时开始运动时，若以点M，D，C为顶点的三角形与以点B，O，N为顶点的三角形相似，求t的值；
（4）过点D与x轴平行的直线，交抛物线的对称轴于点Q，将线段BA沿过点B的直线翻折，点A的对称点为A'，求A'Q+QN+DN的最小值．









答案和解析
1.【答案】C

【解析】解：∵2020×=1
∴2020的倒数是，
故选：C．
根据倒数的定义求解即可
本题考查倒数的定义，熟记倒数的定义是解题的关键．
2.【答案】A

【解析】解：A、球的三视图都是圆，故本选项符合题意；
B、圆锥的主视图和左视图是三角形，俯视图是带有圆心的圆，故本选项不符合题意；
C、圆柱的主视图和左视图是矩形，俯视图是圆，故本选项不符合题意；
D、三棱柱的主视图和左视图是矩形，俯视图是三角形，故本选项不符合题意；
故选：A．
根据主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形解答即可．
本题考查的是几何体的三视图，理解主视图、左视图、俯视图是分别从物体正面、左面和上面看所得到的图形是解题的关键．
3.【答案】D

【解析】解：根据科学记数法的表示形式为a×10n，其中1≤|a|＜10，n为整数，则3450亿=345000000000=3.45×1011．
故选：D．
科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．
本题主要考查利用科学记数法表示较大的数的方法，掌握科学记数法的表示方法是解答本题的关键，这里还需要注意n的取值．
4.【答案】A

【解析】解：由x2-3x+2=0可知，其二次项系数a=1，一次项系数b=-3，
由根与系数的关系：x1+x2=，
故选：A．
本题可利用根与系数的关系，求出该一元二次方程的二次项系数以及一次项系数的值，代入公式求解即可．
本题考查一元二次方程根与系数的关系，求解时可利用常规思路求解一元二次方程，也可以通过韦达定理提升解题效率
5.【答案】D

【解析】解：把点（2，3）代入y=kx（k≠0）得2k=3，
解得，
∴正比例函数解析式为，
设正比例函数平移后函数解析式为，
把点（1，-1）代入得，
∴，
∴平移后函数解析式为，
故函数图象大致为：
．
故选：D．
先求出正比例函数解析式，再根据平移和经过点（1，-1）求出一次函数解析式，即可求解．
本题考查了求正比例函数，一次函数解析式，一次函数图象与性质，根据正比例函数求出平移后一次函数解析式是解题关键．
6.【答案】D

【解析】解：A.，故A选项错误；
B．（-2a2b）3=（-2）3（a2）3b3=-8a6b3，故B选项错误；
C．（a-b）2=a2-2ab+b2，故C选项错误；
D.，故D选项正确．
故选：D．
分别运用二次根式、整式和分式的运算法则逐项排除即可．
本题考查了二次根式、整式和分式的运算，熟练掌握相关运算法则是解题的关键．
7.【答案】A

【解析】解：∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，
∴∠ABD=∠BDC，
∵∠ABE+∠ABD=∠BDC+∠CDF，
∴∠ABE=∠CDF，
A．若添加AE=CF，则无法证明△ABE≌△CDF，故选项A符合题意；
B．若添加∠AEB=∠CFD，运用AAS可以证明△ABE≌△CDF，故选项B不符合题意；
C．若添加∠EAB=∠FCD，运用ASA可以证明△ABE≌△CDF，故选项C不符合题意；
D．若添加BE=DF，运用SAS可以证明△ABE≌△CDF，故选项D不符合题意．
故选：A．
根据平行四边形的性质结合全等三角形的判定，逐项进行判断即可．
本题考查平行四边形的性质、全等三角形的判定和性质等知识，解题的关键是准确寻找全等三角形解决问题，属于中考常考题型．
8.【答案】B

【解析】解：∵a+b＞0，ab＞0，∴a＞0，b＞0．
A、（a，b）在第一象限，因为小手盖住的点在第二象限，故此选项不符合题意；
B、（-a，b）在第二象限，因为小手盖住的点在第二象限，故此选项符合题意；
C、（-a，-b）在第三象限，因为小手盖住的点在第二象限，故此选项不符合题意；
D、（a，-b）在第四象限，因为小手盖住的点在第二象限，故此选项不符合题意；
故选：B．
因为ab＞0，所以a、b同号，又a+b＞0，所以a＞0，b＞0，观察图形判断出小手盖住的点在第二象限，然后解答即可．
本题考查了点的象限的判断，熟练判断a，b的正负是解题的关键．
9.【答案】B

【解析】解：假设不规则图案面积为x，
由已知得：长方形面积为20，
根据几何概率公式小球落在不规则图案的概率为：，
当事件A实验次数足够多，即样本足够大时，其频率可作为事件A发生的概率估计值，故由折线图可知，小球落在不规则图案的概率大约为0.35，
综上有：，解得x=7．
故选：B．
本题分两部分求解，首先假设不规则图案面积为x，根据几何概率知识求解不规则图案占长方形的面积大小；继而根据折线图用频率估计概率，综合以上列方程求解．
本题考查几何概率以及用频率估计概率，并在此基础上进行了题目创新，解题关键在于清晰理解题意，能从复杂的题目背景当中找到考点化繁为简，创新题目对基础知识要求极高
10.【答案】C

【解析】解：∵折叠，且∠P1MA=90°，
∴∠DMP1=∠DMA=45°，即∠ADM=45°，
∵折叠，
∴∠MDP1=∠ADP=∠PDM=∠ADM=22.5°，
∴在△DP1M中，∠DP1M=180°-45°-22.5°=112.5°，
故选：C．
由折叠前后对应角相等且∠P1MA=90°可先求出∠DMP1=∠DMA=45°，进一步求出∠ADM=45°，再由折叠可求出∠MDP1=∠ADP=∠PDM=22.5°，最后在△DP1M中由三角形内角和定理即可求解．
此题主要考查了平行线的性质，本题借助矩形的性质考查了折叠问题、三角形内角和定理等，记牢折叠问题的特点：折叠前后对应边相等，对应角相等即可解题．
11.【答案】2（x+3）（x-3）

【解析】解：2x2-18=2（x2-9）=2（x+3）（x-3），
故答案为：2（x+3）（x-3）．
提公因式2，再运用平方差公式因式分解．
本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．
12.【答案】4

【解析】解：设点A的坐标为（xA，yA），AB⊥y，
由题意可知：，
∴yA•xA=4，
又点A在反比例函数图象上，
故有k=xA•yA=4．
故答案为：4．
根据△OAB的面积等于2，即可得到线段OB与线段AB的乘积，进而得到A点横坐标与纵坐标的乘积，进而求出k值．
本题考查了反比例函数系数k的几何意义，三角形的面积公式等，熟练掌握反比例函数的图形和性质是解决此类题的关键．
13.【答案】甲

【解析】解：甲的“送教上门”时间的平均数为：，
乙的“送教上门”时间的平均数为：，
甲的方差：，
乙的方差：，
因为，
所以甲的方差小，故甲学生每周接受送教的时间更稳定．
故答案为：甲．
先算出甲、乙送教上门时间的平均数，进而求出方差，方差越小，则接受送教的时间更稳定．
本题主要考查方差，熟练掌握方差的意义：方差越小，数据的密集度越高，波动幅度越小是解题的关键．
14.【答案】6.18

【解析】解：由作图得△ABC为直角三角形，CE=BC=AB=5cm，AE=AD，
∴AC=cm，
∴AE=AC-CE=5cm，
∴cm．
故答案为：6.18．
根据作图得△ABC为直角三角形，CE=BC=AB=5cm，AE=AD，根据勾股定理求出AC，再求出AE，即可求出AD．
本题考查了尺规作图，勾股定理等知识，根据作图步骤得到相关已知条件是解题关键．
15.【答案】

【解析】解：由题意可知，第一行三个数的乘积为：，
设第二行中间数为x，则，解得，
设第三行第一个数为y，则，解得，
∴2个空格的实数之积为．
故答案为：．
先将表格中最上一行的3个数相乘得到，然后中间一行的三个数相乘以及最后一行的三个数相等都是，即可求解．
本题考查了二次根数的乘法运算法则，熟练掌握二次根式的加减乘除运算法则是解决此类题的关键．
16.【答案】x（x+12）=864

【解析】解：∵矩形的宽为x，且宽比长少12，
∴矩形的长为（x+12）．
依题意，得：x（x+12）=864．
故答案为：x（x+12）=864．
由矩形的宽及长与宽之间的关系可得出矩形的长为（x+12），再利用矩形的面积公式即可得出关于x的一元二次方程，此题得解．
本题考查了由实际问题抽象出一元二次方程以及数学常识，找准等量关系，正确列出一元二次方程是解题的关键．
17.【答案】13

【解析】解：∵圆锥底面周长=侧面展开后扇形的弧长=10π，
∴OB=，
在Rt△AOB中，AB=，
所以该圆锥的母线长AB为13．
故答案为：13．
由扇形弧长求出底面半径，由勾股定理即可求出母线AB的长．
本题考查圆锥弧长公式的应用，解题的关键是牢记有关的公式．
18.【答案】

【解析】解：如图，分别过点E、C作EH、CG垂直AB，垂足为点H、G，

∵根据题意四边形ABEF为菱形，
∴AB=BE=，
又∵∠ABE=30°
∴在RT△BHE中，EH=，
根据题意，AB∥CF，
根据平行线间的距离处处相等，
∴HE=CG=，
∴Rt△ABC的面积为．
故答案为：．
先利用直角三角形中30°角的性质求出HE的长度，然后利用平行线间的距离处处相等，可得CG的长度，即可求出直角三角形ABC面积．
本题的辅助线是解答本题的关键，通过辅助线，利用直角三角形中的30°角所对直角边是斜边一半的性质，求出HE，再利用平行线间的距离处处相等这一知识点得到HE=CG，最终求出直角三角形面积．
19.【答案】解：原式=1+2+（-1）-2×
=1+2+-1-
=2．

【解析】原式利用零指数幂、负整数指数幂法则，绝对值的代数意义，以及特殊角的三角函数值计算即可求出值．
此题主要考查了根式运算，指数计算，绝对值，三角函数值等知识点，正确应用记住它们的化简规则是解题关键．
20.【答案】解：（1）根据非负数得：m-1=0且n+2=0，
解得：m=1，n=-2，
（2）原式=m2-3mn+m2+4mn+4n2-4n2=2m2+mn，
当m=1，n=-2，原式=2×1+1×（-2）=0．

【解析】（1）m=1，n=-2；
（2）2m2+mn；0．
本题考查了绝对值与二次根式的非负性、整式的化简求值，还涉及去括号法则、完全平方公式、合并同类项法则等知识，熟练掌握非负数的性质以及运算法则是解答的关键．
21.【答案】（1）证明：如图：连接OA，
∵OA=OB，
∴∠OBA=∠OAB，
∵AB=AC，
∴∠OBA=∠C，
∴∠OAB=∠C，
∵∠CAD=∠C，
∴∠OAB=∠CAD，
∵BD是直径，
∴∠BAD=90°，
∵∠OAC=∠BAD-∠OAB+∠CAD=90°，
∴AC是⊙O的切线；

（2）解：由（1）可知AC是⊙O的切线，
∴∠OAC=90°，∠AOD=2∠B，
∵AB=AC，
∴∠B=∠C，
∴∠AOC+∠C=2∠B+∠C=3∠C=90°，
∴∠B=∠C=30°，
在Rt△ABD中，BD===，
∴OB=，
∴⊙O的半径为．

【解析】（1）连接OA，由圆的性质可得OA=OB，即∠OBA=∠OAB；再由AB=AC，即∠OBA=∠C，再结合∠CAD=∠C，可得∠OAB=∠CAD，然后由∠BAD=90°说明∠OAC=90°即可完成证明；
（2）根据等腰三角形的性质和圆的性质即可得到结论．
本题考查了圆的切线的判定，相似三角形的判定和性质，证得∠OAC=90°是解答本题的关键．
22.【答案】解：根据题意知，四边形AA1B1O和四边形BB1C1B2均为矩形，
∴OB1=AA1=62m，B2C1=BB1=100m，
∴BO=BB1-OB1=100-62=38m，CB2=CC1-B2C1=200-100=100m，
在Rt△AOB中，∠AOB=90°，∠BAO=30°，BO=38m，
∴AB=2BO=2×38=76m；
在Rt△CBB2中，∠CB2B=90°，∠CBB2=45°，CB2=100m，
∴，
∴，
即管道AB和BC的总长度为：．

【解析】先根据题意得到BO，CB2的长，在Rt△ABO中，由三角函数可得AB的长度，在Rt△BCB2中，由三角函数可得BC的长度，再相加即可得到答案．
考查了解直角三角形的应用，关键是根据三角函数得到AB和BC的长度．
23.【答案】100  18

【解析】解：（1）15÷15%=100（人）．
故答案为：100；

（2）如图，选B的人数：100-40-15-5=40（人）．
条形图补充如下：


（3）图②中，D选项所对应的扇形圆心角为：360o×=18o．
故答案为：18；

（4）1500×=600（人）．
故估计该校学生“停课不停学”期间平均每天利用网络学习时间在C选项的有600人．
（1）根据选A的有50人，占15%，从而求得本次接受问卷调查的学生总数；
（2）根据各组人数之和等于数据总数求得选B的人数，从而可以将条形统计图补充完整；
（3）用360°乘以D选项所占百分比可得所对应扇形圆心角的度数；
（4）利用样本估计总体，用1500乘以样本中学习时间在C选项的人数所占的百分比即可．
本题考查的是条形统计图和扇形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．也考查了利用样本估计总体．
24.【答案】解：（1）设A型风扇进货的单价是x元，B型风扇进货的单价是y元，
依题意，得：，
解得：．
答：A型风扇进货的单价是10元，B型风扇进货的单价是16元；
（2）设购进A型风扇m台，则购进B型风扇（100-m）台，
依题意，得：，
解得：71≤m≤75，
又∵m为正整数，
∴m可以取72、73、74、75，
∴小丹共有4种进货方案，方案1：购进A型风扇72台，B型风扇28台；方案2：购进A型风扇73台，B型风扇27台；方案3：购进A型风扇74台，B型风扇26台；方案4：购进A型风扇75台，B型风扇25台．

【解析】（1）设A型风扇进货的单价是x元，B型风扇进货的单价是y元，根据“2台A型风扇和5台B型风扇进价共100元，3台A型风扇和2台B型风扇进价共62元”，即可得出关于x，y的二元一次方程组，解之即可得出结论；
（2）设购进A型风扇m台，则购进B型风扇（100-m）台，根据“购进A型风扇不超过B型风扇数量的3倍，购进A、B两种风扇的总金额不超过1170元”，即可得出关于m的一元一次不等式组，解之即可得出m的取值范围，再结合m为正整数即可得出各进货方案．
本题考查了二元一次方程组的应用以及一元一次不等式组的应用，解题的关键是：（1）找准等量关系，正确列出二元一次方程组；（2）根据各数量之间的关系，正确列出一元一次不等式组．
25.【答案】AF=2DM

【解析】解：（1）猜想AF与DM的数量关系是AF=2DM，
理由：∵四边形ABCD是正方形，
∴CD=AD，∠ADC=90°，
在△ADF和△CDE中，
，
∴△ADF≌△CDE（SAS），
∴AF=CE，
∵M是CE的中点，
∴CE=2DM，
∴AF=2DM，
故答案为：AF=2DM；

（2）①AF=2DM仍然成立，
理由如下：延长DM到点N，使MN=DM，连接CN，
∵M是CE中点，
∴CM=EM，
又∠CMN=∠EMD，
∴△MNC≌△MDE（SAS），
∴CN=DE=DF，∠MNC=∠MDE，
∴CN∥DE，
又AD∥BC
∴∠NCB=∠EDA，
∵四边形ABCD是正方形，
∴AD=DC，∠BCD=90°=∠EDF，
∴∠ADF=∠DCN，
∴△ADF≌△DCN（SAS），
∴AF=DN，
∴AF=2DM；
②∵△ADF≌△DCN，
∴∠NDC=∠FAD，
∵∠CDA=90°，
∴∠NDC+∠NDA=90°，
∴∠FAD+∠NDA=90°，
∴AF⊥DM；
③∵α=45°，
∴∠EDC=90°-45°=45°
∵∠EDM=2∠MDC，
∴∠EDM=∠EDC=30°，
∴∠AFD=30°，
过A点作AG⊥FD的延长线于G点，∴∠ADG=90°-45°=45°，

∴△ADG是等腰直角三角形，
设AG=k，则DG=k，AD=AG÷sin45°=k，
FG=AG÷tan30°=k，
∴FD=ED=k-k，
故=．
（1）根据题意合理猜想即可；
（2）①延长DM到点N，使MN=DM，连接CN，先证明△MNC≌△MDE，再证明△ADF≌△DCN，得到AF=DN，故可得到AF=2DM；
②根据全等三角形的性质和直角的换算即可求解；
③依题意可得∠AFD=∠EDM=30°，可设AG=k，得到DG，AD，FG，ED的长，故可求解．
此题主要考查四边形综合，解题的关键是熟知正方形的性质、旋转的特点、全等三角形的判定与性质及三角函数的运用．
26.【答案】解：（1）将C（8，0），B（0，6）代入，得，
解得，
∴抛物线的解析式为：；

（2）如答图1，作DE⊥x于点E，

∵C（8，0），B（0，6），
∴OC=8，OB=6．
∴BC=10．
∵∠BOC=∠BCD=∠DEC，
∴△BOC～△CED．
∴．
∴CE=3，DE=4．
∴OE=OC+CE=11．
∴D（11，4）．

（3）若点M在DA上运动时，DM=5t，ON=4t，
当△BON～△CDM，则，即不成立，舍去；
当△BON～△MDC，则，即，解得：；
若点M在BC上运动时，CM=25-5t．
当△BON～△MCD，则，即，
∴．
当3＜t≤4时，ON=16-4t．
∴，
解得（舍去）．
当4＜t≤5时，ON=4t-16
∴，无解；
当△BON～△DCM，则，即，
∴ON=30-6t；
当3＜t≤4时，ON=16-4t，
∴30-6t=16-4t，
解得t=7（舍去）；
当4＜t≤5时，ON=4t-16，
∴30-6t=4t-16，
解得．
综上所示：当时，△BON～△MDC；时，△BON～△DCM；

（4）如答图2，作点D关于x轴的对称点F，连接QF交x轴于点N，

∵点D（11，4），
∴点F（11，-4）．
由得对称轴为x=5，
∴点Q（5，4）．
∴．
∴．
故A'Q+QN+DN的最小值为．

【解析】（1）将C（8，0），B（0，6）代入计算即可；
（2）作DE⊥x于点E，证明△BOC～△CED，可得CE，DE长度，进而得到点D的坐标；
（3）分为点M在AD，BC上两种情况讨论，当点M在AD上时，分为△BON～△CDM和△BON～△MDC两种情况讨论；当点M在BC上时，分为△BON～△MCD和△BON～△DCM两种情况讨论；
（4）作点D关于x轴的对称F，连接QF，可得QN+DN的最小值；连接BQ减去BA'可得A'Q的最小值，综上可得A'Q+QN+DN的最小值．
本题考查了二次函数与几何图形的综合，涉及相似三角形的性质与判定，最短路径问题的计算，熟知以上知识的应用是解题的关键．