山东省淄博市2021年中考数学二模试卷附答案

这是一份山东省淄博市2021年中考数学二模试卷附答案，共14页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


中考数学二模试卷
一、单选题（共12题；共24分）
1.的值等于（    ）
A.                                        B.                                        C.                                        D. 
2.下面每个图形都是由6个边长相同的正方形拼成的图形，其中能折叠成正方体的是（   ）
A.        B.        C.        D. 
3.下列结论正确的是（     ）
A. 如果a＞b，c＞d，那么a－c＞b－d                   B. 如果a＞b，那么 ＞1
C. 如果a＞b，那么 ＜                                     D. 如果 ＜ ，那么a＜b
4.如图，在 中，对角线 与 相交于点O，E是边 的中点，连接 .若 ，则 的度数为（）

A.                                        B.                                        C.                                        D. 
5.去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵，每棵产量的平均数 (单位：千克)及方差S2(单位：千克2)如表所示：

甲
乙
丙
丁

23
23
24
24
S2
2.1
1.9
2
1.9
今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植，应选的品种是(    )
A. 甲                                         B. 乙                                         C. 丙                                         D. 丁
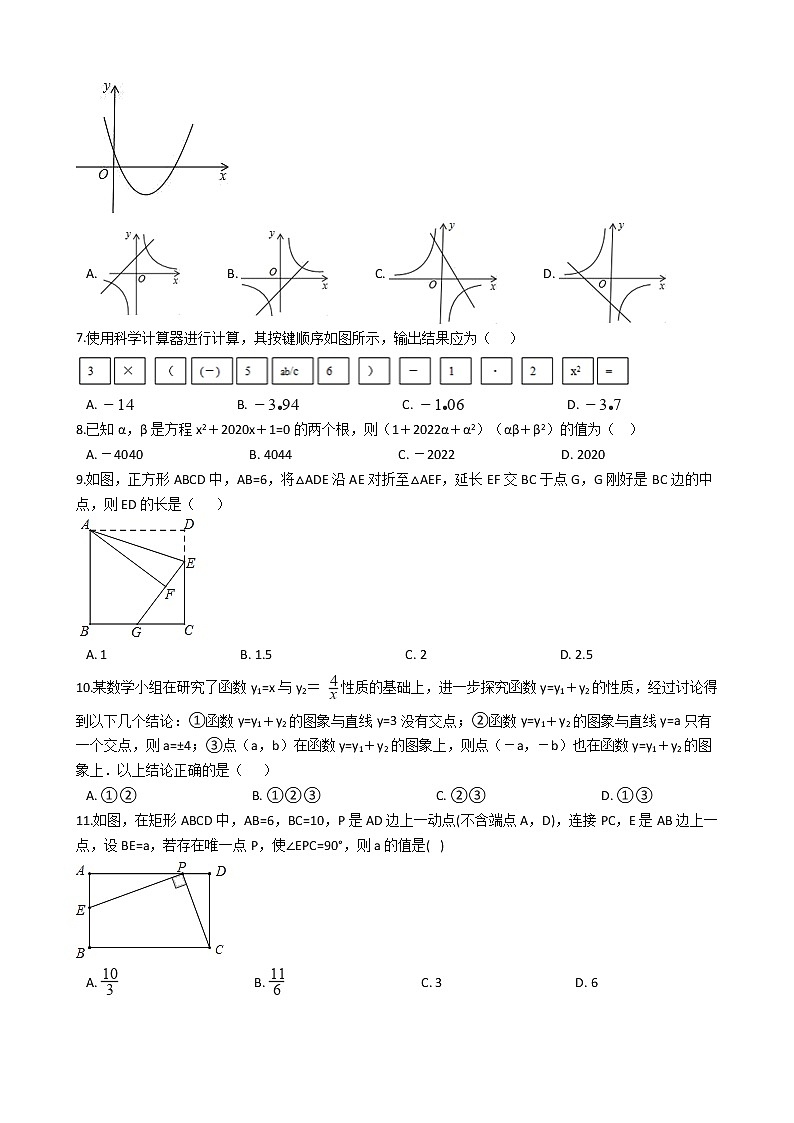
6.已知二次函数y＝ax2+bx+c的图象如图所示，则在同一直角坐标系中，一次函数y＝ax+b和反比例函数 的图象大致是（　　）

A.               B.               C.               D. 
7.使用科学计算器进行计算，其按键顺序如图所示，输出结果应为（    ）

A.                                 B.                                 C.                                 D. 
8.已知α，β是方程x2＋2020x＋1=0的两个根，则（1＋2022α＋α2）（αβ＋β2）的值为（   ）
A. －4040                                 B. 4044                                 C. －2022                                 D. 2020
9.如图，正方形ABCD中，AB=6，将△ADE沿AE对折至△AEF，延长EF交BC于点G，G刚好是BC边的中点，则ED的长是（     ）

A. 1                                          B. 1.5                                          C. 2                                          D. 2.5
10.某数学小组在研究了函数y1=x与y2＝ 性质的基础上，进一步探究函数y=y1＋y2的性质，经过讨论得到以下几个结论：①函数y=y1＋y2的图象与直线y=3没有交点；②函数y=y1＋y2的图象与直线y=a只有一个交点，则a=±4；③点（a，b）在函数y=y1＋y2的图象上，则点（－a，－b）也在函数y=y1＋y2的图象上．以上结论正确的是（     ）
A. ①②                                    B. ①②③                                    C. ②③                                    D. ①③
11.如图，在矩形ABCD中，AB=6，BC=10，P是AD边上一动点(不含端点A，D)，连接PC，E是AB边上一点，设BE=a，若存在唯一点P，使∠EPC=90°，则a的值是(   )

A.                                          B.                                          C. 3                                         D. 6
12.对于二次函数y=ax2－（2a－1）x＋a－1（a≠0），有下列结论：①其图象与x轴一定相交；②其图象与直线y=x－1有且只有一个公共点；③无论a取何值，抛物线的顶点始终在同一条直线上；④无论a取何值，函数图象都经过同一个点．其中正确结论的个数是（     ）
A. 1                                           B. 2                                           C. 3                                           D. 4
二、填空题（共5题；共5分）
13.若am=8，an=2，则am－2n的值是________．
14.如果x2+mx+6＝（x﹣2）（x﹣n），那么m+n的值为________．
15.如图，菱形ABCD，∠B=60°，AB=4，⊙O内切于菱形ABCD，则⊙O的半径为________．

16.如图，已知矩形ABCD，AB＝8，AD＝4，E为CD边上一点，CE＝5，点P从B点出发，以每秒1个单位的速度沿着BA边向终点A运动，连接PE，设点P运动的时间为t秒，则当t的值为________时，△PAE是以PE为腰的等腰三角形．

17.如图，二次函数 的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C ， 其对称轴与x轴交于点D ， 若P为y轴上的一个动点，连接PD ， 则 PC+PD的最小值为________．

三、解答题（共7题；共73分）
18.计算：
19.如图，矩形ABCD中，E是AD的中点，延长CE，与BA的延长线交于点F，连接AC，DF．请判断四边形ACDF的形状，并说明理由．

20.某校创建“环保示范学校”，为了解全校学生参加环保类社团的意愿，在全校随机抽取了50名学生进行问卷调查．问卷给出了五个社团供学生选择(学生可根据自己的爱好选择一个社团，也可以不选)，对选择了社团的学生的问卷情况进行了统计，如下表：
社团名称
A 酵素制作社团
B 回收材料小制作社团
C 垃圾分类社团
D 环保义工社团
E 绿植养护社团
人数
10
15
5
10
5

（1）根据以上信息填空：这5个数的中位数是________；扇形图中没选择的百分比为________；
（2）①补全条形统计图；②若该校有1400名学生，根据调查统计情况，请估计全校有多少学生愿意参加环保义工社团；
（3）若小诗和小雨两名同学在酵素制作社团或绿植养护社团中任意选择一个参加，请用树状图或列表法求出这两名同学同时选择绿植养护社团的概率．
21.某水果店5月份购进甲、乙两种水果共花费1700元，其中甲种水果8元/千克，乙种水果18元/千克.6月份，这两种水果的进价上调为：甲种水果10元/千克，乙种水果20元/千克.
（1）若该店6月份购进这两种水果的数量与5月份都相同，将多支付货款300元，求该店5月份购进甲、乙两种水果分别是多少千克？
（2）若6月份将这两种水果进货总量减少到120千克，且甲种水果不超过乙种水果的3倍，则6月份该店需要支付这两种水果的货款最少应是多少元？
22.如图，一次函数 ，与反比例函数 交于点A（3，1）、B（-1，n），y1交y轴于点C，交x轴于点D．

（1）求反比例函数及一次函数的解析式；
（2）求△OBD的面积；
（3）根据图象直接写出 ＞ 的解集．
23.如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，交AC于点E，过点D作FG⊥AC于点F，交AB的延长线于点G．

（1）求证：GD为⊙O切线；
（2）求证：DE2=EF·AC；
（3）若tanC=2，AB=5，求AE的长．
24.如图，在平面直角坐标系中，抛物线y=ax2+2x+c与x轴交于A（﹣1，0）B（3，0）两点，与y轴交于点C．

（1）求抛物线y=ax2+2x+c的解析式:；
（2）点D为抛物线上对称轴右侧、x轴上方一点，DE⊥x轴于点E，DF∥AC交抛物线对称轴于点F，求DE+DF的最大值；
（3）①在拋物线上是否存在点P，使以点A，P，C为顶点，AC为直角边的三角形是直角三角形？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由；
②点Q在抛物线对称轴上，其纵坐标为t，请直接写出△ACQ为锐角三角形时t的取值范围．

答案解析部分
一、单选题
1.【解析】【解答】解： ＝ ，
故答案为：A.
【分析】根据商的算术平方根等于被除式的算术平方根除以除式的算数平方根。
2.【解析】【解答】解：能折叠成正方体的是

故答案为：C．
【分析】根据正方体的展开图可知，横不过4，凹田弃之，中间四连方，两侧各一个，即可一一判断。
3.【解析】【解答】解： ,A不符合题意；
如果b<0，∵a>b，则 ,B不符合题意；
如果ab<0，∵a>b，则 ,C不符合题意；
如果 ，则 ，D符合题意．
故答案为：D．
【分析】根据不等式的性质对每个选项进行判断求解即可。
4.【解析】【解答】解： °，∠BAC=80°
∠BCA=180°-50°=50°
对角线AC与BD相交于点O，E是CD的中点，
EO是△DBC的中位线
EO∥BC
∠1=∠ACB=50°
故答案为：B.
【分析】先求出 ∠BCA=180°-50°=50°，再求出EO是△DBC的中位线，最后计算求解即可。
5.【解析】【解答】解：∵24＞23，
∴丙，丁产量更高，
又∵2＞1.9，
∴丁更稳定.
故答案为：D.
【分析】先求出丙，丁产量更高，再根据2＞1.9，最后求解即可。
6.【解析】【解答】由二次函数图象可知a＞0，c＞0，
由对称轴x＝﹣ ＞0，可知b＜0，
∴一次函数y＝ax+b的图象经过一、三、四象限，
反比例函数y＝ 的图象在一、三象限．
故答案为：B ．
【分析】先由二次函数的图象判定a＞0，c＞0，再根据其对称轴公式判定b的符号，根据一次函数和反比例函数的性质确定其所在的象限即可.
7.【解析】【解答】解：根据如图所示的按键顺序，输出结果应为3×（- ）-1.22=-2.5-1.44=-3.94，
故答案为：B．
【分析】根据按键顺序，列式计算求解即可。
8.【解析】【解答】解： 是方程 的两个根，
，
，
则 ，
，
，
，
，
故答案为：A.
【分析】由题意把x=α代入一元二次方程可得α2+2020α+1=0，将等式变形得α2=2020α-1，由一元二次方程的根与系数的关系可得αβ==1，然后把α2和αβ代入所求代数式计算即可求解.
9.【解析】【解答】解：如图，连接AG，

∵四边形ABCD是正方形，
∴AB=AD=6，∠B=∠D=90°，
由折叠得：AD=AF，∠D=∠AFE=90°，
∴∠B=∠AFG=90°，AF=AB，
∵Rt△ABG和Rt△AFG中，
AB=AF，AG=AG，
∴Rt△ABG≌Rt△AFG(HL)，
∴BG=GF，
∵G是BC边的中点，∴BG=GC=GF=3
设DE=x，则CE=6−x,CG=3,GE=GF+EF=BG+DE=3+x，
在Rt△ECG中，由勾股定理得： ，即 ，
解方程得：x=2
故答案为：C．
【分析】先求出AD=AF，∠D=∠AFE=90°，再证明Rt△ABG≌Rt△AFG，最后根据勾股定理计算求解即可。
10.【解析】【解答】解：由题意得： ，
联立 ，
整理得： ，
此方程根的判别式为 ，方程没有实数根，
则函数 的图象与直线 没有交点，结论①符合题意；
联立 ，
整理得： ，
函数 的图象与直线 只有一个交点，
关于x的一元二次方程 只有一个实数根，
此方程根的判别式 ，
解得 ，则结论②符合题意；
点 在函数 的图象上，
，
，
点 也在函数 的图象上，则结论③符合题意；
综上，结论正确的是①②③，
故答案为：B．
【分析】先求出，再根据根的判别式及交点，最后对每个结论一一判断即可作答。
11.【解析】【解答】解：∵PE⊥PC，
∴∠APE+∠DPC=90°，
∵∠D=90°，
∴∠DCP+∠DPC=90°，
∴∠APE=∠DCP，又∠A=∠D=90°，
∴△APE∽△DCP，
∴ = ，
设AP=x，AE=y，
可得x(10-x)=6y，
∴x2-10x+6y=0，
由题意△=0，
∴100-24y=0，
∴y= ，
∵BE=AB-AE=6- = ，
故答案为：B．
【分析】设AP=x，AE=y，证明△APE∽△DCP，根据相似三角形的性质得到比例式，转化为一元二次方程，利用判别式△=0，构建方程解决问题．
12.【解析】【解答】解：令ax2－（2a－1）x＋a－1=0，
则 ，
∴ax2－（2a－1）x＋a－1=0有两个不相等的实根，
∴y=ax2－（2a－1）x＋a－1（a≠0）图象与x轴一定相交，①符合题意；
令ax2－（2a－1）x＋a－1=x-1，则ax2－2ax＋a=0，
∵a≠0，∴x2－2x＋1=0，即（x-1）2=0 ，∴ ,
∴y=ax2－（2a－1）x＋a－1（a≠0）图象直线y=x－1有且只有一个公共点，②符合题意；
∵y=ax2－（2a－1）x＋a－1（a≠0）的顶点为 ，
即 ，不难看出，无论a取何值，点 总是在直线y=2(x-1)上，所以③符合题意；
∵当x=1时，y=a-(2a-1)+a-1=a-2a+1+a-1=0,所以无论a取何值，函数图象都经过同一个点（1，0），④符合题意，所以符合题意结论的个数是4．
故答案为：D．
【分析】根据根的判别式和函数图象进行求解即可。
二、填空题
13.【解析】【解答】解： ．
故答案为2．
【分析】根据同底数幂的除法进行计算求解即可。
14.【解析】【解答】解：∵（x﹣2）（x﹣n）＝x2﹣（2+n）x+2n，
∴m＝﹣（2+n），2n＝6，
∴n＝3，m＝﹣5，
∴m+n＝﹣5+3＝﹣2．
故答案为﹣2．
【分析】把（x-2）（x-n）展开，之后利用恒等变形得到方程，即可求解m、n的值，之后可计算m+n的值．
15.【解析】【解答】解：设AB和BC上的切点分别为E、F，连接OA、OE、OB、OF，则 ，

内切于菱形ABCD，

平分


同理得





故答案为：
【分析】先求出OB 平分 ， 再求出AO和OB的长度，最后根据三角形的面积公式计算求解即可。
16.【解析】【解答】解：根据题意得：BP＝t，
∵四边形ABCD是矩形，AB＝8，AD＝4，
∴CD＝AB＝8，BC＝AD＝4，
∴AP＝8﹣t，DE＝DC﹣CE＝8﹣5＝3，
由勾股定理得：AE＝ ＝5，
过E作EF⊥AB于F，

则∠EFA＝∠EFB＝90°，
∵∠C＝∠B＝90°，
∴四边形BCEF是矩形，
∴BF＝CE＝5，BC＝EF＝4，
∴PF＝5﹣t，
由勾股定理得：PE2＝EF2＋PF2＝42＋（5﹣t）2 ，
①当AE＝PE时，52＝42＋（5﹣t）2 ，
解得：t＝2，t＝8，
∵t＝8不符合题意，舍去；
②当AP＝PE时，（8﹣t）2＝42＋（5﹣t）2 ，
解得：t＝ ，
即当t的值为2或 时，△PAE是以PE为腰的等腰三角形，
故答案为：2或 ．
【分析】先求出AE＝ ＝5，再求出PF＝5﹣t，最后分类讨论，进行求解即可。
17.【解析】【解答】解：连接AC
y＝ ﹣ x﹣4与x轴交点A（﹣3，0）、B（5，0），点C（0，﹣4），
∴sin∠ACO＝ ，
作点D关于y轴的对称点D'，作点A关于y轴的对称点A'，过点D'作D'E⊥CA'交于点E ， 则D'E为所求；

由对称性可知，∠ACO＝∠OCA'，
∴sin∠OCA'＝ ，
∴ PC＝PE，
再由D'P＝DP，
∴ PC+PD的最小值为D'E，
∵A'（3，0），D'（﹣1，0），
∴A'D'＝4，CO＝4，A'O＝3，
∴CA'＝5，
∴
∴D'E＝ ；
故答案为: ；
【分析】先求出sin∠ACO＝ ，再根据锐角三角函数和点的坐标进行计算求解即可。
三、解答题
18.【解析】【分析】先算乘方运算，同时化简绝对值，代入特殊角的三角函数值，然后合并即可。
19.【解析】【分析】先求出 ∠FAE=∠CDE， 再求出 AE=DE， 最后证明 △FAE≌△CDE ，即可作答。
20.【解析】【解答】解：（1）这5个数从小到大排列：5，5，10，10，15，故中位数为10．
没有选择的占1-10%-30%-20%-10%-20%=10%
故答案为10；10%
【分析】根据扇形统计图，条形统计图和树状图进行作答求解即可。
21.【解析】【分析】（1）设该店5月份购进甲种水果x千克，购进乙种水果y千克，根据总价=单价×购进数量，即可得出关于x、y的二元一次方程组，解之即可得出结论；（2）设购进甲种水果a千克，需要支付的货款为w元，则购进乙种水果（120﹣a）千克，根据总价=单价×购进数量，即可得出w关于a的函数关系式，由甲种水果不超过乙种水果的3倍，即可得出关于a的一元一次不等式，解之即可得出a的取值范围，再利用一次函数的性质即可解决最值问题.
22.【解析】【分析】（1）利用待定系数法求函数解析式即可；
（2）先求出 OD=2， 再求出 BE=3， 最后利用三角形面积公式进行计算求解即可；
（3）根据函数图象求不等式的解集即可。
23.【解析】【分析】（1）先求出 ∠ABC=∠C， 再求出 OD⊥DF， 最后即可证明求解；
（2）先求出 BD=DE=CD， 再求出 ，即可作答；
（3）先求出 BD=DC=   ，再求出 EF=CF=1，CE=2， 最后进行计算求解即可。
24.【解析】【分析】（1）先求出 a=﹣1， 最后求函数解析式即可；
（2）先求出直线AC的解析式为y=3x+3， 再求出 抛物线对称轴为x=1， 最后进行作答求解即可；
（3）①分类讨论，解方程组求点的坐标即可；
②根据函数图象和锐角三角函数求取值范围即可。