

河南省许昌市七年级下学期数学期末考试试卷
展开
七年级下学期数学期末考试试卷
一、单选题(共10题;共20分)
1.下列式子没有意义的是( )
A. B. C. D.
2.下列方程中,属于二元一次方程的是( )
A. B. C. D.
3.我市某一天的最高气温是 ,最低气温是零下 ,则当天我市气温变化范围 是( )
A. B. C. D.
4.下列调查中,最适合采用抽样调查的是( )
A. 了解全班同学每周体育锻炼的时间 B. 对市场上某一品牌电脑使用寿命的调查
C. 对旅客上飞机前的安检 D. 对“神州十一号”运载火箭发射前的零部件质量状况的调查
5.点 为直线 外一点,点 为直线 上三点, ,则点到直线 的距离为( )
A. B. C. D. 不大于
6.点 在 轴的下方, 轴的左侧,到 轴的距离是 ,到 轴的距离是 ,则点 的坐标是( )
A. B. C. D.
7.在解方程组中 ,①-②所得的方程是( )
A. B. C. D.
8.若 是关于 的一元一次不等式,则该不等式的解集是( )
A. B. C. D.
9.某校学生来自甲、乙、丙三个地区,其人数比为2:3:5,如图所示的扇形图表示上述分布情况.已知来自甲地区的为180人,则下列说法不正确的是( )
A. 扇形甲的圆心角是72° B. 学生的总人数是900人
C. 丙地区的人数比乙地区的人数多180人 D. 甲地区的人数比丙地区的人数少180人
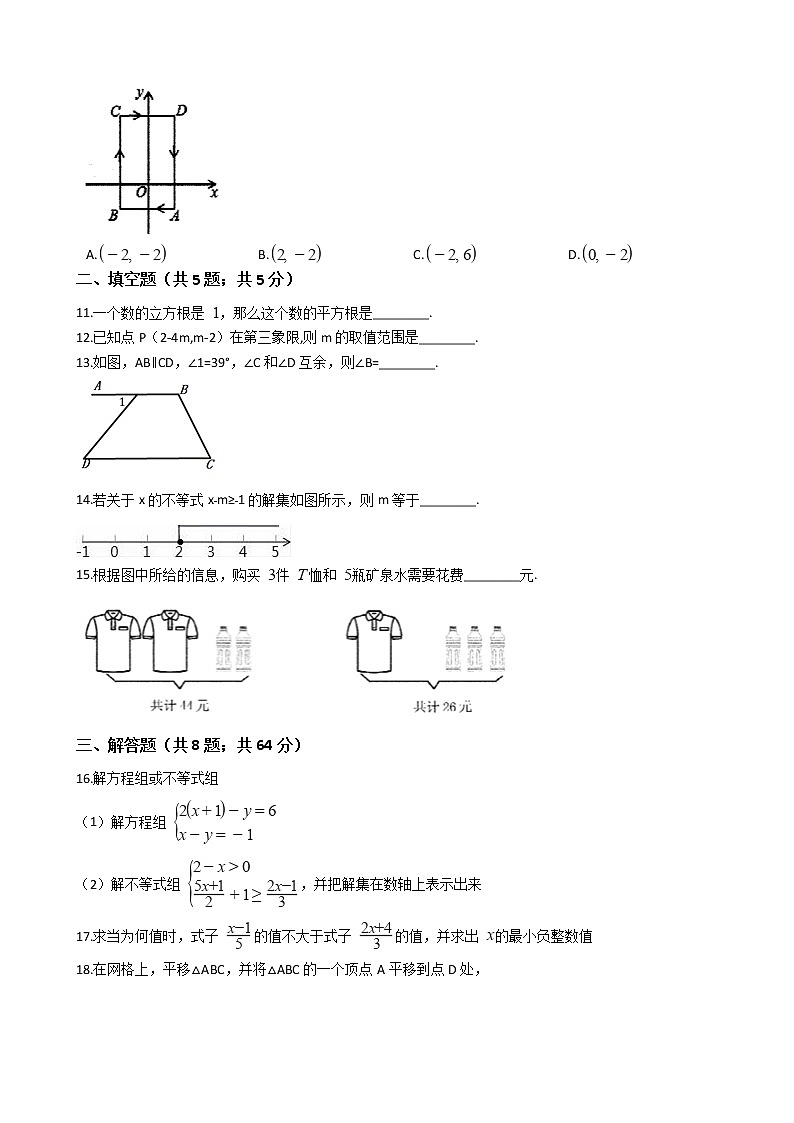
10.如图,平面直角坐标系中,一蚂蚁从 点出发,沿着 循环爬行,其中 点的坐标为 , 点的坐标为 , 点的坐标为 , 点的坐标为 ,当蚂蚁爬了 个单位时,蚂蚁所处位置的坐标为( )
A. B. C. D.
二、填空题(共5题;共5分)
11.一个数的立方根是 ,那么这个数的平方根是________.
12.已知点P(2-4m,m-2)在第三象限,则m的取值范围是________.
13.如图,AB∥CD,∠1=39°,∠C和∠D互余,则∠B=________.
14.若关于x的不等式x﹣m≥﹣1的解集如图所示,则m等于________.
15.根据图中所给的信息,购买 件 恤和 瓶矿泉水需要花费________元.
三、解答题(共8题;共64分)
16.解方程组或不等式组
(1)解方程组
(2)解不等式组 ,并把解集在数轴上表示出来
17.求当为何值时,式子 的值不大于式子 的值,并求出 的最小负整数值
18.在网格上,平移△ABC,并将△ABC的一个顶点A平移到点D处,
(1)请你作出平移后的图形△DEF;
(2)请求出△DEF的面积(每个网格是边长为1的正方形).
19.已知方程组 的解满足 为非正数, 为负数
(1)求 的取值范围
(2)化简:
20.在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了________名同学;
(2)条形统计图中,m=________,n=________;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是________度;
(4)学校计划购买课外读物6000册,请根据样本数据,估计学校购买其他类读物多少册比较合理?
21.如图,CD AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,问直线EF与AB有怎样的位置关系,为什么?
22.夏否来临,我市某电器超市购进 两种型号的电风扇,每台进价分别为 元、 元,下表是近两周的销售情况:(进价、售价均保持不变,利润=销售收入-进货成本).
销售时段 | 销售数量 | 销售收入 | |
种型号 | 种型号 | ||
第一周 | 台 | 台 | 元 |
第二周 | 台 | 台 | 元 |
(1)求 两种型号的电风扇的销售单价;
(2)若超市准备再采购这两种型号的电风扇只 台,这 台电风扇全部售出后,若利润不低于 元,求 种型号的电风扇至少要采购多少台?
23.阅读理解题
先阅读理解下面的问题,再按要求完成下列问题
例:解不等式
解:由有理数的乘法法则“两数相乘,同号得正”有① 或②
解不等式组①,得
解不等式组②,得
所以不等式 的解集为 或
解不等式:
答案解析部分
一、单选题
1.【解析】【解答】A、被开方数是正数,该式子有意义,故本选项正确,不合题意;
B、被开方数是负数,该式子无意义,故本选项错误,符合题意;
C、(-3)2=9,被开方数是正数,该式子有意义,故本选项正确,不合题意;
D、三次根式的被开方数可以是任何数,该式子有意义,故本选项正确,不合题意.
故答案为:B.
【分析】根据立方根和平方根的性质可得答案.
2.【解析】【解答】解:A. 是二元一次方程,此选项符合题意;
B. 不是整式方程,不是二元一次方程,此选项不符合题意;
C. 中xy项的次数是2,不是二元一次方程,此选项不符合题意;
D. 中 项的次数是2,不是二元一次方程,此选项不符合题意;
故答案为:A.
【分析】含有两个未知数,并且未知项的最高次是1的整式方程,叫做二元一次方程,据此逐一判断即可.
3.【解析】【解答】最高气温是 表示的是气温小于或等于 ,
最低气温是零下 表示的是气温大于或等于 ,
则当天我市气温变化范围是 ,
故答案为:D.
【分析】 由于最高气温是 , 最低气温是零下 ,直接写出范围即可.
4.【解析】【解答】A.了解全班同学每周体育锻炼的时间,适合全面调查;
B.对市场上某一品牌电脑使用寿命的调查,有破坏性,适合抽样调查;
C.对旅客上飞机前的安检,需要全面调查;
D. 对“神州十一号”运载火箭发射前的零部件质量状况的调查,需要全面调查;
【分析】一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
5.【解析】【解答】解:当PC⊥m时,PC是点P到直线m的距离,即点P到直线m的距离2cm,
当PC不垂直直线m时,点P到直线m的距离小于PC的长,即点P到直线m的距离小于2cm,
综上所述:点P到直线m的距离不大于2cm,
故答案为:D.
【分析】根据点到直线的距离是直线外的点与直线上垂足间的线段的长,再根据垂线段最短,可得答案.
6.【解析】【解答】解:∵点A在x轴的下方,y轴的左侧,
∴点A在第三象限,
∵点A到x轴的距离是3,到y轴的距离是2,
∴点A的横坐标为−2,纵坐标为−3,
∴点A的坐标是(−2,−3).
故答案为:A.
【分析】先判断出点A在第三象限,再根据点到x轴的距离等于其纵坐标的绝对值,到y轴的距离等于其横坐标的绝对值解答.
7.【解析】【解答】在解方程组 中,①−②所得的方程是x=3,
故答案为:C.
【分析】方程组中两方程相减得到结果,即可作出判断.
8.【解析】【解答】解:∵ 是关于x的一元一次不等式,
∴3+m=1,
∴m=-2,
∴-6-5x>4,
∴该不等式的解集是 ;
故答案为:C.
【分析】根据一元一次不等式的定义得出3+m=1,求出m的值,再把m的值代入原式,再解不等式即可.
9.【解析】【解答】A.根据甲区的人数是总人数的 ,则扇形甲的圆心角是: ×360°=72°,故此选项正确,不符合题意;
B.学生的总人数是:180÷ =900人,故此选项正确,不符合题意;
C.丙地区的人数为:900× =450,,乙地区的人数为:900× =270,则丙地区的人数比乙地区的人数多450-270=180人,故此选项正确,不符合题意;
D.甲地区的人数比丙地区的人数少270-180=90人,故此选项错误,符合题意.
故答案为:D.
【分析】A、利用360°乘以甲区的人数占总人数的比值即得;
B、利用甲地区的人数除以甲区的人数占总人数的比值即得;
C、先分别求出乙、丙地区的人数,然后由丙地区的人数减去乙地区人数即得;
D、先求出甲地区的人数减去丙地区的人数,然后比较即得.
10.【解析】【解答】解:∵A点坐标为(2,﹣2),B点坐标为(﹣2,﹣2),C点坐标为(﹣2,6),
∴AB=2﹣(﹣2)=4,BC=6﹣(﹣2)=8,
∴从A→B→C→D→A一圈的长度为2(AB+BC)=24.
∵2020=84×24+4,
∴当蚂蚁爬了2020个单位时,它所处位置在点A左边4个单位长度处,即(-2,﹣2).
故答案为:A
【分析】根据蚂蚁的爬行规律找到蚂蚁爬行一循环的长度是24,∵2020=84×24+4,∴当蚂蚁爬了2020个单位时,它所处位置在点A左边4个单位长度处,即可解题.
二、填空题
11.【解析】【解答】13=1,± =±1,
故答案为:±1.
【分析】根据立方跟乘方运算,可得被开方数,根据开方运算,可得平方根.
12.【解析】【解答】点在第三象限的条件是:横坐标是负数,纵坐标是负数.可得2-4m<0,m-2<0,解得 .
【分析】根据第三象限点的坐标特征:横坐标是负数,纵坐标是负数,据此得出不等式组,然后求出解集即可.
13.【解析】【解答】∵AB∥CD, ∠1=39°,
∴∠D=∠1=39°
∵∠C和∠D互余,
∴∠C=90°-39°=51°
∵AB∥CD,
∴∠B=180°-51°=129°.
故答案为 .
【分析】根据两直线平行,内错角相等,可得∠D=∠1=39°,利用余角的性质求出∠C=90°-39°=51°,利用两直线平行,同旁内角互补,可得∠B+∠C=180°,从而求出∠B的度数.
14.【解析】【解答】关于x的不等式x-m≥-1,
得x≥m-1,
由题目中的数轴表示可知:
不等式的解集是:x≥2,
因而可得到,m-1=2,
解得,m=3.
故答案是:3.
【分析】首先解得关于x的不等式x-m≥-1的解集即x≥m-1,然后观察数轴上表示的解集,求得m的值即可.
15.【解析】【解答】设每件T恤价格和每瓶矿泉水的价格分别为x元,y元,
则 ,
解得 .
故购买3件T恤和5瓶矿泉水需要花费为20×3+2×5=70元.
故答案为:70.
【分析】通过理解图形可知本题存在两个等量关系,即每件T恤价格×2+每瓶矿泉水的价格×2=44,每件T恤价格+每瓶矿泉水的价格×3=26.根据这两个等量关系可列出方程组.
三、解答题
16.【解析】【分析】(1)①−②求出x=5,把x=5代入①求出y即可;(2)先求出不等式组的解集,再在数轴上表示出不等式组的解集即可.
17.【解析】【分析】根据题意列出不等式,解之求出x的范围即可得出答案.
18.【解析】【分析】(1)根据点A到点D移动的方向和距离,可确定出点B和点C平移后对应点的位置,从而可画出平移后的图形;
(2)利用割补法,根据△DEF的面积等于一个长为4,宽为3的长方形的面积分别减去周围三个直角三角形的面积即可算出答案。
19.【解析】【分析】(1)先求出方程组的解,根据x为非正数,y为负数,组成不等式组,解不等式组,即可解答;(2)根据m的取值范围,绝对值的性质化简,即可解答.
20.【解析】【解答】解:(1)根据条形图得出文学类人数为:70,利用扇形图得出文学类所占百分比为:35%,
故本次调查中,一共调查了:70÷35%=200人,
故答案为:200;
⑵根据科普类所占百分比为:30%,
则科普类人数为:n=200×30%=60人,
m=200﹣70﹣30﹣60=40人,
故m=40,n=60;
故答案为:40,60;
⑶艺术类读物所在扇形的圆心角是: ×360°=72°,
故答案为:72;
【分析】(1)结合两个统计图,根据条形图得出文学类人数为:70,利用扇形图得出文学类所占百分比为:35%,即可得出总人数;(2)利用科普类所占百分比为:30%,则科普类人数为:n=200×30%=60人,即可得出m的值;(3)根据艺术类读物所在扇形的圆心角是: ×360°=72°;(4)根据喜欢其他类读物人数所占的百分比,即可估计6000册中其他读物的数量;
21.【解析】【分析】两直线的位置关系有两种:平行或者相交,根据图形可猜想两直线平行,然后根据已知条件探求平行的判定条件,即可证明结论.
22.【解析】【分析】(1)设 种型号的电风扇的销售单价为 元/台, 种型号的电风扇的销售单价为 元/台根据两周收入可得: ,解方程组可得;(2)设采购 种型号电风扇 台,则采购 种型号的电风扇 台,根据利润不低于 元,可得 ;
23.【解析】【分析】先根据有理数的除法法则“两数相除,异号得负”可得两个一元一次不等式组,再求出两个不等式组的解集即可得.
2021河南省许昌市一模数学试卷无答案: 这是一份2021河南省许昌市一模数学试卷无答案,共6页。
2022河南省许昌市初三一模数学试卷及答案: 这是一份2022河南省许昌市初三一模数学试卷及答案,文件包含许昌市2022年一模数学试卷pdf、九年级一模数学参考答案许昌市2022年pdf等2份试卷配套教学资源,其中试卷共10页, 欢迎下载使用。
2021年河南省许昌市中考数学二模试卷: 这是一份2021年河南省许昌市中考数学二模试卷,共27页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












