

江苏省江阴市2019-2020学年七年级下学期期末考试数学试题 (解析版)
展开2019-2020学年江苏省无锡市江阴市七年级第二学期期末数学试卷
一、选择题
1.下列运算正确的是( )
A.(x3)4=x7 B.x2•x3=x5 C.x4÷x=x4 D.x+x2=x3
2.若a<b,则下列不等式一定成立的是( )
A.a+2c<b+2c B.2c﹣a<2c﹣b C.a+2c>b+2c D.2ac<2bc
3.下列各式从左到右的变形,属于因式分解的是( )
A.(x+1)(x﹣1)=x2﹣1 B.x2﹣y2=(x+y)(x﹣y)
C.x2﹣2x+1=x(x﹣2)+1 D.x2+y2=(x+y)2
4.如图,点B、C、D在同一直线上,AB∥CE,若∠A=55°,∠ACB=65°,则∠1的值为( )
A.80° B.65° C.60° D.55°
5.一个多边形的内角和是外角和的2倍,这个多边形是( )
A.四边形 B.五边形 C.六边形 D.八边形
6.下列各式计算正确的是( )
A.(x+y)2=x2+y2 B.(x+3)(x﹣3)=x2﹣3
C.(m﹣n)(n﹣m)=n2﹣m2 D.(x﹣y)2=(y﹣x)2
7.不等式3x<﹣4(x﹣6)的正整数解的个数为( )
A.1个 B.2个 C.3个 D.4个
8.给出下列4个命题:①四边形的内角和等于外角和;②有两个角互余的三角形是直角三角形;③若|x|=2,则x=2;④同旁内角的平分线互相垂直.其中真命题的个数为( )
A.1个 B.2个 C.3个 D.4个
9.某校春季运动会比赛中,七年级(1)班、(2)班的竞技实力相当,关于比赛结果,甲同学说:(1)班与(2)班得分比为2:1;乙同学说:(1)班得分比(2)班得分多38分.若设(1)班得x分,(2)班得y分,根据题意所列的方程组应为( )
A. B.
C. D.
10.如图,长方形ABCD中,AB=3cm,BC=2cm,点P从A出发,以1cm/s的速度沿A→B→C运动,最终到达点C,在点P运动了3秒后点Q开始以2cm/s的速度从D运动到A,在运动过程中,设点P的运动时间为t,则当△APQ的面积为2cm2时,t的值( )
A.2或 B.2或 C.1或 D.1或
二、填空题(本大题共8小题,每小题2分,共16分)
11.水珠不断地滴在石头上,形成小洞,平均每年小洞增加的深度约为0.00096m,数据0.00096用科学记数法可表示为 .
12.若am=2,an=3,则am+n的值是 .
13.写出二元一次方程x+3y=11的一个整数解 .
14.命题“如果ab=0,则a=0”的逆命题是 .
15.△ABC两边a=3,b=6,则第三边c的取值范围为 .
16.若x,y互为相反数,且3x﹣y=4,则xy的值为 .
17.在一个多边形中,小于120度的内角最多有 个.
18.已知关于x的不等式组(a为整数)的所有整数解的和S满足21.6≤S<33.6,则所有这样的a的和为 .
三、解答题(本大题共8小题,共64分.解答时应写出文字说明、证明过程或演算步骤)
19.计算:
(1)(﹣1)2020+(3﹣π)0﹣()﹣1;
(2)a2•a4+a8÷a2﹣(﹣2a2)3.
20.把下面各式分解因式:
(1)x2﹣4xy+4y2;
(2)3a3﹣27a.
21.(1)解方程组
(2)解不等式组
22.先化简,再求值:(2x+y)2﹣(3x﹣y)2+5(x+y)(x﹣y),其中x=,y=2.
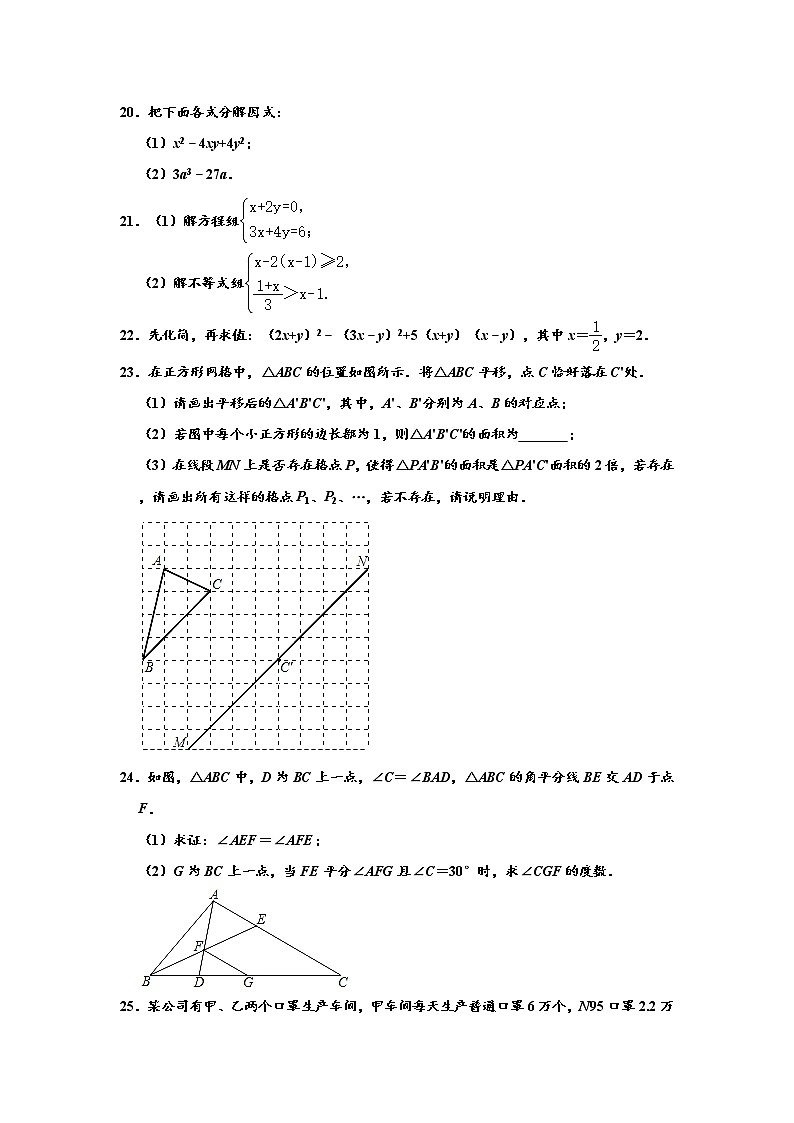
23.在正方形网格中,△ABC的位置如图所示.将△ABC平移,点C恰好落在C'处.
(1)请画出平移后的△A'B'C',其中,A'、B'分别为A、B的对应点;
(2)若图中每个小正方形的边长都为1,则△A'B'C'的面积为 ;
(3)在线段MN上是否存在格点P,使得△PA'B'的面积是△PA'C'面积的2倍,若存在,请画出所有这样的格点P1、P2、…,若不存在,请说明理由.
24.如图,△ABC中,D为BC上一点,∠C=∠BAD,△ABC的角平分线BE交AD于点F.
(1)求证:∠AEF=∠AFE;
(2)G为BC上一点,当FE平分∠AFG且∠C=30°时,求∠CGF的度数.
25.某公司有甲、乙两个口罩生产车间,甲车间每天生产普通口罩6万个,N95口罩2.2万个.乙车间每天生产普通口罩和N95口罩共10万个,且每天生产的普通口罩比N95口罩多6万个.
(1)求乙车间每天生产普通口罩和N95口罩各多少万个?
(2)现接到市防疫指挥部要求:需要该公司提供至少156万个普通口罩和尽可能多的N95口罩.因受原料和生产设备的影响,两个车间不能同时生产,且当天只能确保一个车间的生产.已知该公司恰好用20天完成防疫指挥部下达的任务.
问:①该公司至少安排乙车间生产多少天?
②该公司最多能提供多少个N95口罩?
26.如图,直角三角形纸片ABC中,∠C=90°,将纸片沿EF折叠,使得A点落在BC上点D处,连接DE,DF.△CDE中有两个内角相等.
(1)若∠A=50°,求∠BDF的度数;
(2)若△BDF中也有两个内角相等,求∠B的度数.
参考答案
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列运算正确的是( )
A.(x3)4=x7 B.x2•x3=x5 C.x4÷x=x4 D.x+x2=x3
解:∵(x3)4=x12≠x7,x2•x3=x5,x4÷x=x3≠x4,
x+x3≠x4,
∴选项B正确.
故选:B.
2.若a<b,则下列不等式一定成立的是( )
A.a+2c<b+2c B.2c﹣a<2c﹣b C.a+2c>b+2c D.2ac<2bc
解:A、∵a<b,∴a+2c<b+2c,原变形一定成立,故此选项符合题意;
B、∵a<b,∴2c﹣a>2c﹣b,原变形不成立,故此选项不符合题意;
C、∵a<b,∴a+2c<b+2c,原变形不成立,故此选项不符合题意;
D、∵a<b,∴2ac<2bc(c>0)或2ac=2bc(c=0)或2ac>2bc(c<0),原变形不一定成立,故此选项不符合题意;
故选:A.
3.下列各式从左到右的变形,属于因式分解的是( )
A.(x+1)(x﹣1)=x2﹣1 B.x2﹣y2=(x+y)(x﹣y)
C.x2﹣2x+1=x(x﹣2)+1 D.x2+y2=(x+y)2
解:A、(x+1)(x﹣1)=x2﹣1,属于整式的乘法运算,故本选项错误;
B、x2﹣y2=(x+y)(x﹣y),符合因式分解的定义,故本选项正确;
C、x2﹣2x+1=x(x﹣2)+1,不符合因式分解的定义,故本选项错误;
D、x2+2xy+y2=(x+y)2,因式分解的过程错误,故本选项错误;
故选:B.
4.如图,点B、C、D在同一直线上,AB∥CE,若∠A=55°,∠ACB=65°,则∠1的值为( )
A.80° B.65° C.60° D.55°
解:如图,∵∠A=55°,∠ACB=65°,
∴∠B=180°﹣55°﹣65°=60°.
∵AB∥CE,
∴∠1=∠B=60°.
故选:C.
5.一个多边形的内角和是外角和的2倍,这个多边形是( )
A.四边形 B.五边形 C.六边形 D.八边形
解:设所求正n边形边数为n,由题意得
(n﹣2)•180°=360°×2
解得n=6.
则这个多边形是六边形.
故选:C.
6.下列各式计算正确的是( )
A.(x+y)2=x2+y2 B.(x+3)(x﹣3)=x2﹣3
C.(m﹣n)(n﹣m)=n2﹣m2 D.(x﹣y)2=(y﹣x)2
解:A.(x+y)2=x2++2xy+y2,故本选项不合题意;
B.(x+3)(x﹣3)=x2﹣9,故本选项不合题意;
C.(m﹣n)(n﹣m)=﹣n2+2mn﹣m2,故本选项不合题意;
D.(x﹣y)2=(y﹣x)2,正确.
故选:D.
7.不等式3x<﹣4(x﹣6)的正整数解的个数为( )
A.1个 B.2个 C.3个 D.4个
解:3x<﹣4(x﹣6),
3x<﹣4x+24,
7x<24,
x<
故正整数解有3,2,1共3个,
故选:C.
8.给出下列4个命题:①四边形的内角和等于外角和;②有两个角互余的三角形是直角三角形;③若|x|=2,则x=2;④同旁内角的平分线互相垂直.其中真命题的个数为( )
A.1个 B.2个 C.3个 D.4个
解:①四边形的内角和和外角和都是360°,
∴四边形的内角和等于外角和,是真命题;
②有两个角互余的三角形是直角三角形,是真命题;
③若|x|=2,则x=±2,本说法是假命题;
④两直线平行时,同旁内角的平分线互相垂直,本说法是假命题;
故选:B.
9.某校春季运动会比赛中,七年级(1)班、(2)班的竞技实力相当,关于比赛结果,甲同学说:(1)班与(2)班得分比为2:1;乙同学说:(1)班得分比(2)班得分多38分.若设(1)班得x分,(2)班得y分,根据题意所列的方程组应为( )
A. B.
C. D.
解:设(1)班得x分,(2)班得y分,
由题意可得,,
即,
故选:D.
10.如图,长方形ABCD中,AB=3cm,BC=2cm,点P从A出发,以1cm/s的速度沿A→B→C运动,最终到达点C,在点P运动了3秒后点Q开始以2cm/s的速度从D运动到A,在运动过程中,设点P的运动时间为t,则当△APQ的面积为2cm2时,t的值( )
A.2或 B.2或 C.1或 D.1或
解:∵四边形ABCD是矩形,
∴∠BAD=90°,AD=BC=2cm,
分两种情况:
①点P在AB上时,点Q在D处,如图1所示:
∵△APQ的面积为2cm2,
∴×t×2=2,
解得:t=2;
②点P在BC上时,如图2所示:
∵△APQ的面积为2cm2,
∴×AQ×3=2,
解得:AQ=,
∴DQ=AD﹣AQ=2﹣==2(t﹣3),
解得:t=;
综上所述,当△APQ的面积为2cm2时,t的值为2或;
故选:A.
二、填空题(本大题共8小题,每小题2分,共16分)
11.水珠不断地滴在石头上,形成小洞,平均每年小洞增加的深度约为0.00096m,数据0.00096用科学记数法可表示为 .
解:0.00096=9.6×10﹣4.
故答案为:9.6×10﹣4.
12.若am=2,an=3,则am+n的值是 6 .
解:am+n=am•an=2×3=6.
故答案为:6.
13.写出二元一次方程x+3y=11的一个整数解 .
解:当x=8时,8+3y=11,
∴y=1.
故是方程x+3y=11的一个整数解;
当x=5时,5+3y=11,
∴y=2.
故是方程x+3y=11的一个整数解;
…
由于二元一次方程有无数个整数解,
所以答案不唯一.
故答案为:(答案不唯一).
14.命题“如果ab=0,则a=0”的逆命题是 .
解:命题“如果ab=0,则a=0”的逆命题是“如果a=0,则ab=0”,
故答案为:如果a=0,则ab=0.
15.△ABC两边a=3,b=6,则第三边c的取值范围为 .
解:∵△ABC两边a=3,b=6,
∴根据三角形的三边关系,得:6﹣3<c<3+6,
即:3<c<9.
故答案为:3<c<9.
16.若x,y互为相反数,且3x﹣y=4,则xy的值为 .
解:∵x,y互为相反数,
∴x+y=0,
即x=﹣y,
∵3x﹣y=4,
∴﹣3y﹣y=4,
解得y=﹣1,
∴x=1,
∴xy=﹣1×1=﹣1.
故答案为﹣1.
17.在一个多边形中,小于120度的内角最多有 个.
解:∵多边形的内角小于120°,
∴外角大于60°,
∴这个多边形小于120°的内角的个数<360°÷60°=6,
∴在一个多边形中,小于120度的内角最多有5个.
故答案为:5.
18.已知关于x的不等式组(a为整数)的所有整数解的和S满足21.6≤S<33.6,则所有这样的a的和为 .
解:,
∵解不等式①得:x>a﹣1,
解不等式②得:x≤a+5,
∴不等式组的解集为a﹣1<x≤a+5,
∴不等式组的整数解a,a+1,a+2,a+3,a+4,a+5,
∵所有整数解的和S满足21.6≤S<33.6,
∴21.6≤6a+15≤33.6,
∴1.1≤a≤3.1,
∴a的值为2,3,
∴2+3=5,
故答案为5.
三、解答题(本大题共8小题,共64分.解答时应写出文字说明、证明过程或演算步骤)
19.计算:
(1)(﹣1)2020+(3﹣π)0﹣()﹣1;
(2)a2•a4+a8÷a2﹣(﹣2a2)3.
解:(1)(﹣1)2020+(3﹣π)0﹣()﹣1
=1+1﹣2
=0;
(2)a2•a4+a8÷a2﹣(﹣2a2)3
=a6+a6+8a6
=10a6.
20.把下面各式分解因式:
(1)x2﹣4xy+4y2;
(2)3a3﹣27a.
解:(1)原式=(x﹣2y)2;
(2)原式=3a(a2﹣9)
=3a(a+3)(a﹣3).
21.(1)解方程组
(2)解不等式组
解:(1),
②﹣①×2,得:x=6,
将x=6代入①,得:6+2y=0,
解得y=﹣3,
则;
(2)解不等式x﹣2(x﹣1)≥2,得:x≤0,
解不等式>x﹣1,得:x<2,
则不等式组的解集为x≤0.
22.先化简,再求值:(2x+y)2﹣(3x﹣y)2+5(x+y)(x﹣y),其中x=,y=2.
解:原式=4x2+4xy+y2﹣(9x2﹣6xy+y2)+5(x2﹣y2)
=4x2+4xy+y2﹣9x2+6xy﹣y2+5x2﹣5y2
=10xy﹣5y2,
当x=,y=2时,原式=10××2﹣5×22=10﹣20=﹣10.
23.在正方形网格中,△ABC的位置如图所示.将△ABC平移,点C恰好落在C'处.
(1)请画出平移后的△A'B'C',其中,A'、B'分别为A、B的对应点;
(2)若图中每个小正方形的边长都为1,则△A'B'C'的面积为 ;
(3)在线段MN上是否存在格点P,使得△PA'B'的面积是△PA'C'面积的2倍,若存在,请画出所有这样的格点P1、P2、…,若不存在,请说明理由.
【解答】 解:(1)如图所示;
(2)△A'B'C'的面积为:3×4﹣2×1﹣4×1×3×3=,
故答案为:;
(3)存在,如图所示,点即为所求P1、P2.
24.如图,△ABC中,D为BC上一点,∠C=∠BAD,△ABC的角平分线BE交AD于点F.
(1)求证:∠AEF=∠AFE;
(2)G为BC上一点,当FE平分∠AFG且∠C=30°时,求∠CGF的度数.
解:(1)证明:∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABF+∠BAD=∠CBE+∠C,
∵∠AFE=∠ABF+∠BAD,∠AEF=∠CBE+∠C,
∴∠AEF=∠AFE;
(2)∵FE平分∠AFG,
∴∠AFE=∠GFE,
∵∠AEF=∠AFE,
∴∠AEF=∠GFE,
∴FG∥AC,
∵∠C=30°,
∴∠CGF=180°﹣∠C=150°.
25.某公司有甲、乙两个口罩生产车间,甲车间每天生产普通口罩6万个,N95口罩2.2万个.乙车间每天生产普通口罩和N95口罩共10万个,且每天生产的普通口罩比N95口罩多6万个.
(1)求乙车间每天生产普通口罩和N95口罩各多少万个?
(2)现接到市防疫指挥部要求:需要该公司提供至少156万个普通口罩和尽可能多的N95口罩.因受原料和生产设备的影响,两个车间不能同时生产,且当天只能确保一个车间的生产.已知该公司恰好用20天完成防疫指挥部下达的任务.
问:①该公司至少安排乙车间生产多少天?
②该公司最多能提供多少个N95口罩?
解:(1)设乙车间每天生产普通口罩x万个,乙车间每天生产N95口罩y万个,
依题意得:.
解得.
答:乙车间每天生产普通口罩8万个,乙车间每天生产N95口罩2万个;
(2)①设安排乙车间生产m天,则甲车间生产(20﹣m)天,
依题意得:8m+6(20﹣m)≥156.
解得m≥18.
答:该公司至少安排乙车间生产18天.
②由题意得,乙车间生产的天数可能是18,19或20天.即有三种生产方案:
方案一:乙车间生产18天,甲车间生产2天;
方案二:乙车间生产19天,甲车间生产1天;
方案三:乙车间生产20天,甲车间生产0天;
则生产的N95口罩=2×20=40(个).
答:该公司最多能提供40个N95口罩.
26.如图,直角三角形纸片ABC中,∠C=90°,将纸片沿EF折叠,使得A点落在BC上点D处,连接DE,DF.△CDE中有两个内角相等.
(1)若∠A=50°,求∠BDF的度数;
(2)若△BDF中也有两个内角相等,求∠B的度数.
解:(1)∵∠C=90°,且△CDE中有两个内角相等,
∴∠CED=∠CDE=45°,
∵△EDF是由△EAF翻折得到,∠A=50°,
∴∠EDF=∠A=50°,
∴∠BDF=180°﹣∠CDE﹣∠EDF=180°﹣45°﹣50°=85°;
(2)设∠EDF=∠EAF=x°,
∴∠BDF=180°﹣45°﹣x°=(135﹣x)°,∠B=(90﹣x)°,
∴∠BFD=180°﹣(135﹣x)°﹣(90﹣x)°=(2x﹣45)°,
∵△BDF中有两个内角相等,可分三种情况讨论:
①当∠BDF=∠B时,令135﹣x=90﹣x,则方程无解,
∴此情况不成立,舍去;
②当∠BFD=∠B时,令2x﹣45=90﹣x,
解得x=45,
∴∠B=90°﹣45°=45°;
③当∠BFD=∠BDF时,令2x﹣45=135﹣x,
解得x=60,
∴∠B=90°﹣60°=30°,
综上所述,若△BDF中也有两个内角相等,则∠B的度数可能为45°或30°.
天津市和平区2019-2020学年七年级下学期期末考试数学试题+解析版: 这是一份天津市和平区2019-2020学年七年级下学期期末考试数学试题+解析版,共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
江苏省江阴市长泾片2023-2024学年七年级下学期期中考试数学试题(原卷版+解析版): 这是一份江苏省江阴市长泾片2023-2024学年七年级下学期期中考试数学试题(原卷版+解析版),文件包含江苏省江阴市长泾片2023-2024学年七年级下学期期中考试数学试题原卷版docx、江苏省江阴市长泾片2023-2024学年七年级下学期期中考试数学试题解析版docx等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。
江苏省无锡市江阴市2023-2024学年八年级下学期期中数学试题(原卷版+解析版): 这是一份江苏省无锡市江阴市2023-2024学年八年级下学期期中数学试题(原卷版+解析版),文件包含江苏省无锡市江阴市2023-2024学年八年级下学期期中数学试题原卷版docx、江苏省无锡市江阴市2023-2024学年八年级下学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。












