

还剩8页未读,
继续阅读
湖北省襄阳八年级下学期数学期末考试试卷
展开
这是一份湖北省襄阳八年级下学期数学期末考试试卷,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
八年级下学期数学期末考试试卷
一、选择题(共10题;共20分)
1.二次根式 中的x的取值范围是( )
A. x<﹣2 B. x≤﹣2 C. x>﹣2 D. x≥﹣2
2.下列二次根式中能与2 合并的是( )
A. B. C. D.
3.在直角三角形中,若勾为3,股为4,则弦为( )
A. 5 B. 6 C. 7 D. 8
4.某学习小组9名学生参加“数学竞赛”,他们的得分情况如下表:
人数(人)
1
3
4
1
分数(分)
80
85
90
95
那么这9名学生所得分数的众数和中位数分别是( )
A. 90,87.5 B. 90,85 C. 90,90 D. 85,85
5.某组数据的方差 中,则该组数据的总和是( )
A. 20 B. 5 C. 4 D. 2
6.已知点(-1,y1),(1,y2),(-2,y3)都在直线y=-x上,则y1 , y2 , y3的大小关系是( )
A. .y1>y2>y3 B. y1<y2<y3 C. y3>y1>y2 D. y3<y1<y2
7.在 中,E,F是对角线AC上不同的两点,下列条件中,不能得出四边形BEDF一定为平行四边形的是( )
A. B. C. D.
8.如图,在 中, , , .点D,E,F分别是相应边上的中点,则四边形DFEB的周长等于( )
A. 8 B. 9 C. 12 D. 13
9.如图,直线y=kx+3经过点(2,0),则关于x的不等式kx+3>0的解集是( )
A. x>2 B. x<2 C. x≥2 D. x≤2
10.如图,在平面直角坐标系中,OABC的顶点A在x轴上,定点B的坐标为(8,4),若直线经过点D(2,0),且将平行四边形OABC分割成面积相等的两部分,则直线DE的表达式是( )
A. y=x-2 B. y=2x-4 C. y=x-1 D. y=3x-6
二、填空题(共6题;共7分)
11.计算6 -15 的结果是________.
12.若以二元一次方程 的解为坐标的点(x,y) 都在直线 上,则常数b=________.
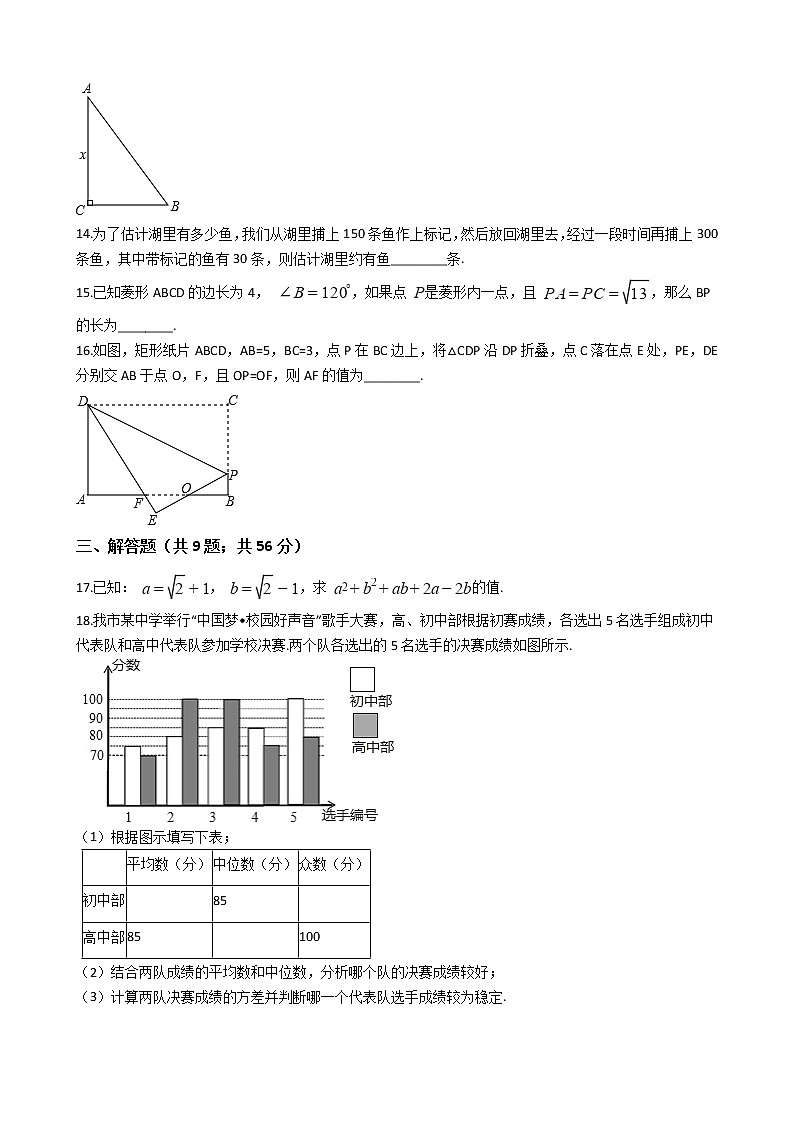
13.《九章算术》是我国古代重要的数学著作之一,在“勾股”中记载了一道“折竹抵地”问题:“今有竹高一丈,未折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长,如果设AC=x,则可列方程求出AC的长为________.
14.为了估计湖里有多少鱼,我们从湖里捕上150条鱼作上标记,然后放回湖里去,经过一段时间再捕上300条鱼,其中带标记的鱼有30条,则估计湖里约有鱼________条.
15.已知菱形ABCD的边长为4, ,如果点 是菱形内一点,且 ,那么BP的长为________.
16.如图,矩形纸片ABCD,AB=5,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE,DE分别交AB于点O,F,且OP=OF,则AF的值为________.
三、解答题(共9题;共56分)
17.已知: , ,求 的值.
18.我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
(1)根据图示填写下表;
平均数(分)
中位数(分)
众数(分)
初中部
85
高中部
85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
19.如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子 的长为13米,此人以0.5米/秒的速度收绳,6秒后船移动到点D的位置,问船向岸边移动了大约多少米?(假设绳子是直的,结果精确到0.1米,参考数据: , )
20.已知一次函数 的图象如图所示,
(1)求 的值;
(2)在同一坐标系内画出函数 的图象;
(3)利用(2)中你所面的图象,写出 时, 的取值范围.
21.如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC , AE∥DC , EF⊥CD于点F .
(1)求证:四边形AECD是菱形;
(2)若AB=5,AC=12,求EF的长.
22.如图,矩形ABCD中,E是AD的中点,延长CE、BA交于点F,连接AC、DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.
23.某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.
(1) 求y与x之间的函数表达式,并写出x的取值范围;
(2) 若该节能产品的日销售利润为W(元),求W与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第几天的日销售利润最大,最大日销售利润是多少元?
24.在正方形ABCD中,过点A引射线AH,交边CD于点H(H不与点D重合).通过翻折,使点B落在射线AH上的点G处,折痕AE交BC于E,连接E,G并延长 交 于F.
(1)如图1,当点H与点C重合时, 与 的大小关系是________; 是________三角形.
(2)如图2,当点H为边CD上任意一点时(点H与点C不重合).连接AF,猜想FG与FD的大小关系,并证明你的结论.
(3)在图2,当 , 时,求 的面积.
25.如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.
(1)菱形ABCO的边长________
(2)求直线AC的解析式;
(3)动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,
①当0<t< 时,求S与t之间的函数关系式;
②在点P运动过程中,当S=3,请直接写出t的值.
答案解析部分
一、选择题
1.【答案】 D
2.【答案】 B
3.【答案】 A
4.【答案】 C
5.【答案】 A
6.【答案】 C
7.【答案】 D
8.【答案】 B
9.【答案】 B
10.【答案】 A
二、填空题
11.【答案】 6 -
12.【答案】 2
13.【答案】
14.【答案】 1500
15.【答案】 1或3
16.【答案】
三、解答题
17.【答案】 解:∵ , ,∴ , .
∴原式 .
18.【答案】 (1)解:
平均数(分)
中位数(分)
众数(分)
初中部
85
85
85
高中部
85
80
100
(2)解:初中部成绩好些。
∵两个队的平均数都相同,初中部的中位数高,
∴在平均数相同的情况下中位数高的初中部成绩好些。
(3)解:∵ ,
,
∴ < ,因此,初中代表队选手成绩较为稳定。
19.【答案】 解:∵在 中, , , ,
∴ .
∵此人以0.5m/s的速度收绳,6s后船移动到点D的位置,
∴ .
∴ .
∴ .
答:船向岸边移动了大约3.3m.
20.【答案】 (1)由图象可知, , .
将 , 两点代入 中,
得 ,解得 .
(2)对于函数 ,
列表:
x
0
1
y
﹣2
0
图象如图:
(3)由图象可得:当 时,x的取值范围为: .
21.【答案】 (1)证明:∵AD∥BC,AE∥DC,
∴四边形AECD是平行四边形,
∵∠BAC=90°,E是BC的中点,
∴AE=CE= BC,
∴四边形AECD是菱形
(2)解:过A作AH⊥BC于点H,
∵∠BAC=90°,AB=5,AC=12,
∴BC=13,
∵ ,
∴ ,
∵点E是BC的中点,四边形AECD是菱形,
∴CD=CE,
∵S▱AECD=CE•AH=CD•EF,
∴
22.【答案】 (1)证明:∵四边形ABCD是矩形,∴AB∥CD,∴∠FAE=∠CDE.
∵E是AD的中点,∴AE=DE.
又∵∠FEA=∠CED,∴△FAE≅△CDE(AAS),
∴CD=FA.
又∵CD∥AF,
∴四边形ACDF是平行四边形.
(2)BC=2CD.
理由如下:
∵CF平分∠BCD,∴∠DCE=45°.
∵∠CDE=90°,∴△CDE是等腰直角三角形,
∴CD=DE,
∵E是AD的中点,∴AD=2CD.
∵AD=BC,∴BC=2CD.
23.【答案】 (1)设线段AB段所表示的函数关系式为y=ax+b(1≤x≤10);
BC段表示的函数关系式为y=mx+n(10<x≤30),
把(1,300)、(10,120)带入y=ax+b中得 ,解得 ,
∴线段AB表示的函数关系式为y=-20x+320(1≤x≤10);
把(10,120),(30,400)代入y=mx+n中得 ,解得 ,
∴线段BC表示的函数关系式为y=14x-20(10<x≤30),
综上所述 .
(2)由题意可知单件商品的利润为10-6=4(元/件),
∴当1≤x≤10时,w=4×(-20x+320)=-80x+1280;
当10<x≤30时,w=4×(14x-20)=56x-80,
∴ ,日销售利润不超过1040元,即w≤1040,
∴当1≤x≤10时,w=-80x+1280≤1040,解得x≥3;
当10<x≤30时,w=56x-80≤1040,解得x≤20,
∴3≤x≤20,∴日销售利润不超过1040元的天数共有18天.
(3)当5≤x≤17,第5天的日销售利润最大,最大日销售利润是880元.
24.【答案】 (1);等腰直角
(2)连接AF,
∵四边形ABCD是正方形的对角线,∴ , .
由翻折可知 , .
∵ ,∴ .
∴ .
(3)设 ,则 , .
在 中, ,即 .
解得 ,即 的长为 .
∴ ;…
∴ .…
25.【答案】 (1)5
(2)解:∵四边形ABCO是菱形,
∴OC=OA=AB=5,即C(5,0).
设直线AC的解析式y=kx+b,函数图象过点A、C,得
,解得 ,
直线AC的解析式y=﹣ x+
(3)解:设M到直线BC的距离为h,当x=0时,y= ,即M(0, ),HM=HO﹣OM=4﹣ = ,由S△ABC=S△AMB+SBMC= AB•OH= AB•HM+ BC•h,×5×4= ×5× + ×5h,解得h= ,
①当0<t< 时,BP=BA﹣AP=5﹣2t,HM=OH﹣OM= ,
S= BP•HM= × (5﹣2t)=﹣ t+ ;
②当2.5<t≤5时,BP=2t﹣5,h= ,
S= BP•h= × (2t﹣5)= t﹣ ,
把S=3代入①中的函数解析式得,3=﹣ t+ ,
解得:t= ,把S=3代入②的解析式得,3= t﹣ ,解得:t= .∴t= 或 .
八年级下学期数学期末考试试卷
一、选择题(共10题;共20分)
1.二次根式 中的x的取值范围是( )
A. x<﹣2 B. x≤﹣2 C. x>﹣2 D. x≥﹣2
2.下列二次根式中能与2 合并的是( )
A. B. C. D.
3.在直角三角形中,若勾为3,股为4,则弦为( )
A. 5 B. 6 C. 7 D. 8
4.某学习小组9名学生参加“数学竞赛”,他们的得分情况如下表:
人数(人)
1
3
4
1
分数(分)
80
85
90
95
那么这9名学生所得分数的众数和中位数分别是( )
A. 90,87.5 B. 90,85 C. 90,90 D. 85,85
5.某组数据的方差 中,则该组数据的总和是( )
A. 20 B. 5 C. 4 D. 2
6.已知点(-1,y1),(1,y2),(-2,y3)都在直线y=-x上,则y1 , y2 , y3的大小关系是( )
A. .y1>y2>y3 B. y1<y2<y3 C. y3>y1>y2 D. y3<y1<y2
7.在 中,E,F是对角线AC上不同的两点,下列条件中,不能得出四边形BEDF一定为平行四边形的是( )
A. B. C. D.
8.如图,在 中, , , .点D,E,F分别是相应边上的中点,则四边形DFEB的周长等于( )
A. 8 B. 9 C. 12 D. 13
9.如图,直线y=kx+3经过点(2,0),则关于x的不等式kx+3>0的解集是( )
A. x>2 B. x<2 C. x≥2 D. x≤2
10.如图,在平面直角坐标系中,OABC的顶点A在x轴上,定点B的坐标为(8,4),若直线经过点D(2,0),且将平行四边形OABC分割成面积相等的两部分,则直线DE的表达式是( )
A. y=x-2 B. y=2x-4 C. y=x-1 D. y=3x-6
二、填空题(共6题;共7分)
11.计算6 -15 的结果是________.
12.若以二元一次方程 的解为坐标的点(x,y) 都在直线 上,则常数b=________.
13.《九章算术》是我国古代重要的数学著作之一,在“勾股”中记载了一道“折竹抵地”问题:“今有竹高一丈,未折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长,如果设AC=x,则可列方程求出AC的长为________.
14.为了估计湖里有多少鱼,我们从湖里捕上150条鱼作上标记,然后放回湖里去,经过一段时间再捕上300条鱼,其中带标记的鱼有30条,则估计湖里约有鱼________条.
15.已知菱形ABCD的边长为4, ,如果点 是菱形内一点,且 ,那么BP的长为________.
16.如图,矩形纸片ABCD,AB=5,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE,DE分别交AB于点O,F,且OP=OF,则AF的值为________.
三、解答题(共9题;共56分)
17.已知: , ,求 的值.
18.我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
(1)根据图示填写下表;
平均数(分)
中位数(分)
众数(分)
初中部
85
高中部
85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
19.如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子 的长为13米,此人以0.5米/秒的速度收绳,6秒后船移动到点D的位置,问船向岸边移动了大约多少米?(假设绳子是直的,结果精确到0.1米,参考数据: , )
20.已知一次函数 的图象如图所示,
(1)求 的值;
(2)在同一坐标系内画出函数 的图象;
(3)利用(2)中你所面的图象,写出 时, 的取值范围.
21.如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC , AE∥DC , EF⊥CD于点F .
(1)求证:四边形AECD是菱形;
(2)若AB=5,AC=12,求EF的长.
22.如图,矩形ABCD中,E是AD的中点,延长CE、BA交于点F,连接AC、DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.
23.某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.
(1) 求y与x之间的函数表达式,并写出x的取值范围;
(2) 若该节能产品的日销售利润为W(元),求W与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第几天的日销售利润最大,最大日销售利润是多少元?
24.在正方形ABCD中,过点A引射线AH,交边CD于点H(H不与点D重合).通过翻折,使点B落在射线AH上的点G处,折痕AE交BC于E,连接E,G并延长 交 于F.
(1)如图1,当点H与点C重合时, 与 的大小关系是________; 是________三角形.
(2)如图2,当点H为边CD上任意一点时(点H与点C不重合).连接AF,猜想FG与FD的大小关系,并证明你的结论.
(3)在图2,当 , 时,求 的面积.
25.如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.
(1)菱形ABCO的边长________
(2)求直线AC的解析式;
(3)动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,
①当0<t< 时,求S与t之间的函数关系式;
②在点P运动过程中,当S=3,请直接写出t的值.
答案解析部分
一、选择题
1.【答案】 D
2.【答案】 B
3.【答案】 A
4.【答案】 C
5.【答案】 A
6.【答案】 C
7.【答案】 D
8.【答案】 B
9.【答案】 B
10.【答案】 A
二、填空题
11.【答案】 6 -
12.【答案】 2
13.【答案】
14.【答案】 1500
15.【答案】 1或3
16.【答案】
三、解答题
17.【答案】 解:∵ , ,∴ , .
∴原式 .
18.【答案】 (1)解:
平均数(分)
中位数(分)
众数(分)
初中部
85
85
85
高中部
85
80
100
(2)解:初中部成绩好些。
∵两个队的平均数都相同,初中部的中位数高,
∴在平均数相同的情况下中位数高的初中部成绩好些。
(3)解:∵ ,
,
∴ < ,因此,初中代表队选手成绩较为稳定。
19.【答案】 解:∵在 中, , , ,
∴ .
∵此人以0.5m/s的速度收绳,6s后船移动到点D的位置,
∴ .
∴ .
∴ .
答:船向岸边移动了大约3.3m.
20.【答案】 (1)由图象可知, , .
将 , 两点代入 中,
得 ,解得 .
(2)对于函数 ,
列表:
x
0
1
y
﹣2
0
图象如图:
(3)由图象可得:当 时,x的取值范围为: .
21.【答案】 (1)证明:∵AD∥BC,AE∥DC,
∴四边形AECD是平行四边形,
∵∠BAC=90°,E是BC的中点,
∴AE=CE= BC,
∴四边形AECD是菱形
(2)解:过A作AH⊥BC于点H,
∵∠BAC=90°,AB=5,AC=12,
∴BC=13,
∵ ,
∴ ,
∵点E是BC的中点,四边形AECD是菱形,
∴CD=CE,
∵S▱AECD=CE•AH=CD•EF,
∴
22.【答案】 (1)证明:∵四边形ABCD是矩形,∴AB∥CD,∴∠FAE=∠CDE.
∵E是AD的中点,∴AE=DE.
又∵∠FEA=∠CED,∴△FAE≅△CDE(AAS),
∴CD=FA.
又∵CD∥AF,
∴四边形ACDF是平行四边形.
(2)BC=2CD.
理由如下:
∵CF平分∠BCD,∴∠DCE=45°.
∵∠CDE=90°,∴△CDE是等腰直角三角形,
∴CD=DE,
∵E是AD的中点,∴AD=2CD.
∵AD=BC,∴BC=2CD.
23.【答案】 (1)设线段AB段所表示的函数关系式为y=ax+b(1≤x≤10);
BC段表示的函数关系式为y=mx+n(10<x≤30),
把(1,300)、(10,120)带入y=ax+b中得 ,解得 ,
∴线段AB表示的函数关系式为y=-20x+320(1≤x≤10);
把(10,120),(30,400)代入y=mx+n中得 ,解得 ,
∴线段BC表示的函数关系式为y=14x-20(10<x≤30),
综上所述 .
(2)由题意可知单件商品的利润为10-6=4(元/件),
∴当1≤x≤10时,w=4×(-20x+320)=-80x+1280;
当10<x≤30时,w=4×(14x-20)=56x-80,
∴ ,日销售利润不超过1040元,即w≤1040,
∴当1≤x≤10时,w=-80x+1280≤1040,解得x≥3;
当10<x≤30时,w=56x-80≤1040,解得x≤20,
∴3≤x≤20,∴日销售利润不超过1040元的天数共有18天.
(3)当5≤x≤17,第5天的日销售利润最大,最大日销售利润是880元.
24.【答案】 (1);等腰直角
(2)连接AF,
∵四边形ABCD是正方形的对角线,∴ , .
由翻折可知 , .
∵ ,∴ .
∴ .
(3)设 ,则 , .
在 中, ,即 .
解得 ,即 的长为 .
∴ ;…
∴ .…
25.【答案】 (1)5
(2)解:∵四边形ABCO是菱形,
∴OC=OA=AB=5,即C(5,0).
设直线AC的解析式y=kx+b,函数图象过点A、C,得
,解得 ,
直线AC的解析式y=﹣ x+
(3)解:设M到直线BC的距离为h,当x=0时,y= ,即M(0, ),HM=HO﹣OM=4﹣ = ,由S△ABC=S△AMB+SBMC= AB•OH= AB•HM+ BC•h,×5×4= ×5× + ×5h,解得h= ,
①当0<t< 时,BP=BA﹣AP=5﹣2t,HM=OH﹣OM= ,
S= BP•HM= × (5﹣2t)=﹣ t+ ;
②当2.5<t≤5时,BP=2t﹣5,h= ,
S= BP•h= × (2t﹣5)= t﹣ ,
把S=3代入①中的函数解析式得,3=﹣ t+ ,
解得:t= ,把S=3代入②的解析式得,3= t﹣ ,解得:t= .∴t= 或 .












