2021学年21.2.1 配方法一等奖ppt课件

这是一份2021学年21.2.1 配方法一等奖ppt课件，共22页。PPT课件主要包含了知识回顾，学习目标，配方法的应用．，课堂导入，这个方程怎么解呢，完全平方公式，知识点，新知探究，问题解决，跟踪训练等内容，欢迎下载使用。

用直接开平方法解下列方程：(1) 9x2=9； (2) (3x+2)2−49=0； (3) 81(2x−5)2−16=0．
先化成(x+p)2=m(m≥0)的形式，再直接开平方.
1．理解一元二次方程配方的方法．
2．掌握用配方法解一元二次方程．
读诗词解题： (通过列方程，算出周瑜去世时的年龄)大江东去浪淘尽，千古风流数人物．而立之年督东吴，早逝英年两位数．十位恰小个位三，个位平方与寿符．哪位学子算得快，多少年华属周瑜？
解：设周瑜去世时的年龄的个位数字为x，则十位数字为x−3．
整理，得x2−11x+30=0.
列方程，得x2=10(x−3)+x.
二次项系数为 1 的完全平方式，常数项等于一次项系数一半的平方．
x2＋2bx＋b2＝(x＋b)2 x2－2bx＋b2＝(x－b)2
a2＋2ab＋b2＝(a＋b)2 a2－2ab＋b2＝(a－b)2
根据以上公式完成填空： (1) x2–4x+____=(x–____)2 (2) x2+12x+____=(x+____)2 (3) y2–8y+____=(y–____)2
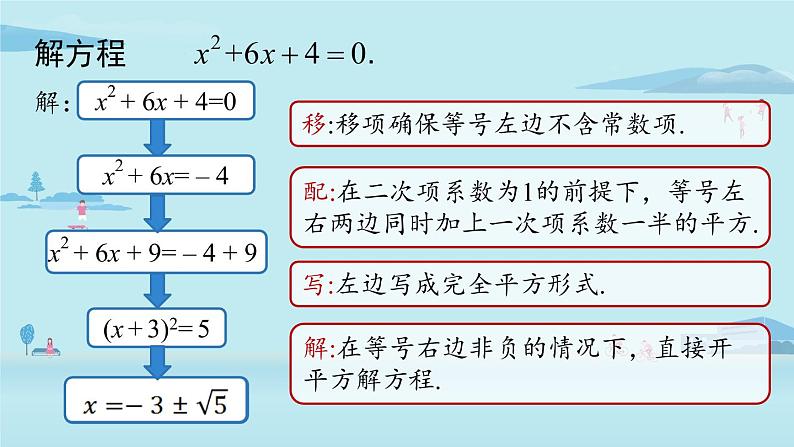
x2 + 6x + 4=0
x2 + 6x + 9= – 4 + 9
(x + 3)2= 5
移:移项确保等号左边不含常数项.
配:在二次项系数为1的前提下，等号左右两边同时加上一次项系数一半的平方.
写:左边写成完全平方形式.
解:在等号右边非负的情况下，直接开平方解方程.
x2 + 6x= – 4
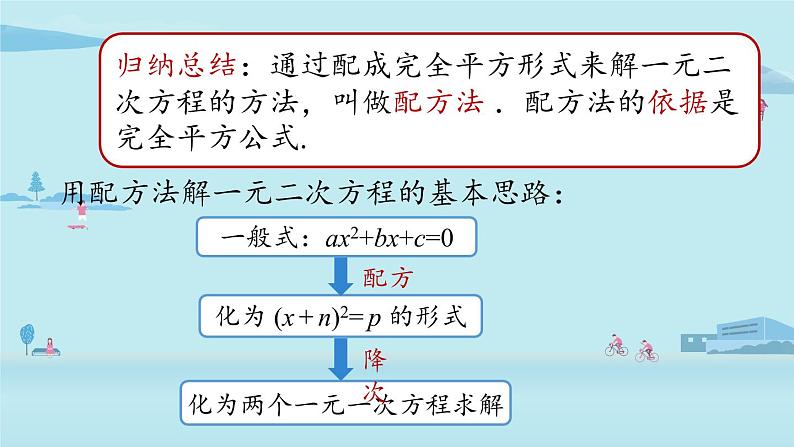
归纳总结：通过配成完全平方形式来解一元二次方程的方法，叫做配方法 ．配方法的依据是完全平方公式.
用配方法解一元二次方程的基本思路：
一般式：ax2+bx+c=0
化为 (x + n)2= p 的形式
化为两个一元一次方程求解
一般地，如果一个一元二次方程通过配方转化成 (x＋n)2＝p (Ⅱ)的形式，那么就有：
(2)当 p＝0 时，方程(Ⅱ)有两个相等的实数根 x1＝x2＝－n；
(3)当 p<0 时，因为对任意实数 x ，都有 (x＋n)2≥0，所以方程(Ⅱ)无实数根．
大江东去浪淘尽，千古风流数人物．而立之年督东吴，早逝英年两位数．十位恰小个位三，个位平方与寿符．哪位学子算得快，多少年华属周瑜？
整理,得x2−11x+30=0,
列方程,得x2=10(x−3)+x，
(通过列方程，算出周瑜去世时的年龄) ：
解得x1=5, x2=6.
当x=5时,周瑜的年龄为25岁,不到而立之年,不符合题意,舍去；当x=6时，周瑜的年龄为36岁，符合题意.所以周瑜去世时的年龄为36岁．
解：(1)移项，得x2－8x＝－1．　 　　　　　
例1 解下列方程：(1)x2－8x＋1＝0； (2)2x2＋1＝3x； (3)3x2－6x＋4＝0．
　　　 配方，得x2－8x＋42＝－1＋42，　　　　　　　 (x－4)2＝15．
(2)2x2＋1＝3x；
解：(2)移项，得2x2-3x=-1.
即 .
解：(3)移项，得 3x2－6x＝－4，　　
(3)3x2－6x＋4＝0．
注意：在(x+n)2=p中，只有当p≥0时，才能直接开平方，p<0时，直接下结论方程无实数根.
因为实数的平方不会是负数，所以x取任何实数时， (x-1)2 都是非负数,上式都不成立,即原方程无实数根．　　　　
用配方法解一元二次方程的一般步骤：
解：(2) 去括号，得x2+4x=8x+12， 移项、合并同类项，得x2－4x＝12，
配方，得x2－4x＋4＝12＋4，
即(x－2)2＝16，
由此可得x－2＝±4，
所以x1＝6，x2＝－2．
解下列方程： (1)x2－x－ ＝0； (2)x(x＋4)＝8x＋12．
1． 通过配成完全平方形式来解一元二次方程的方法,叫做配方法．
2． 用配方法解一元二次方程的一般步骤： 一移 → 二化 → 三配→ 四开．
1.已知x2-10x+y2-16y+89=0，求 的值.
解：由已知x2-10x+y2-16y+89=0，得
x2-10x+25+y2-16y+64=0，
所以(x-5)2+(y-8)2=0，
由完全平方的非负性可得x-5=0且y-8=0，
方程中二次项有两个，考虑将方程左边按字母分组，分别配方后，根据非负数的性质求x和y的值.
2.用配方法证明多项式：-2x2+6x-5的值恒小于0.
证明：-2x2+6x-5=-2(x2-3x)-5
所以-2x2+6x-5的值恒小于0.
二次多项式的配方：一提:提出二次项系数
二配:括号内先加上一次项系数一半的平方，再减去一次项系数一半的平方.
三写:写成a(x+n)2+p的形式，注意符号.
1.一元二次方程 配方后可化为( )A． B．C． D．
2.若将一元二次方程 x2－8x－9＝0 化成 (x+n)2=d 的形式，则n= ，d= ．
x2－8x－9＝0，
x2－8x+ 42 =9+ 42 ，
n=- 4，d=25．