初中数学人教版九年级上册24.1.1 圆完整版课件ppt

这是一份初中数学人教版九年级上册24.1.1 圆完整版课件ppt，共27页。PPT课件主要包含了学习目标，课堂导入，知识点1，新知探究，半径一般用r表示，有间隙吗，半径相同圆心不同，圆心相同半径不同，确定一个圆的要素，跟踪训练等内容，欢迎下载使用。

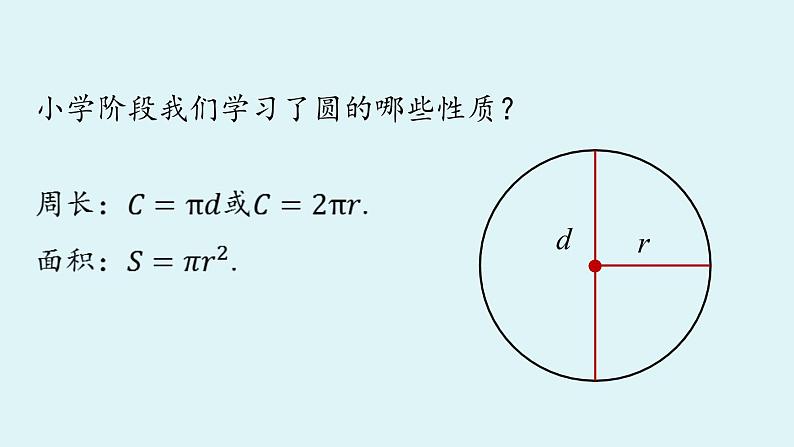
小学阶段我们学习了圆的哪些性质？
1.掌握圆的定义、表示方法及圆具有的特性。
2.理解弦、弧、半圆、优弧、劣弧、同心圆、等圆、等弧等与圆有关的概念，并了解它们之间的区别和联系.
圆是常见的图形，生活中的许多物体都给我们以圆的形象(如图).
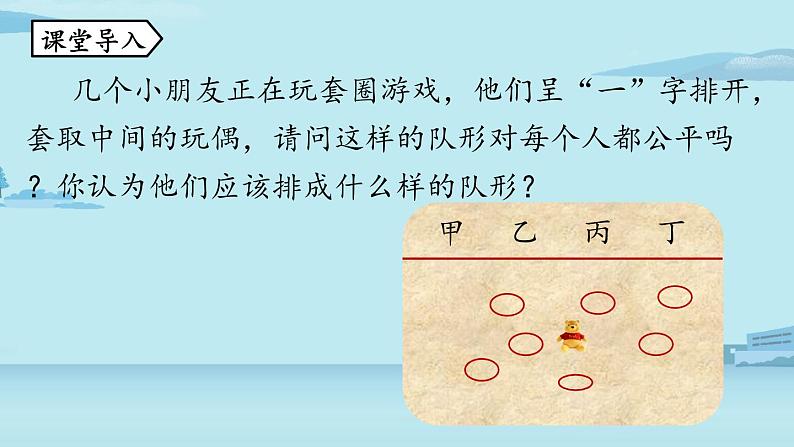
几个小朋友正在玩套圈游戏，他们呈“一”字排开，套取中间的玩偶，请问这样的队形对每个人都公平吗？你认为他们应该排成什么样的队形？
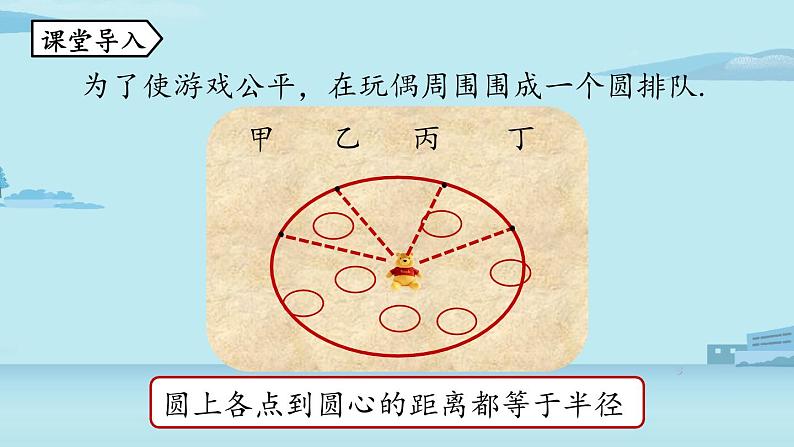
为了使游戏公平，在玩偶周围围成一个圆排队.
圆上各点到圆心的距离都等于半径
既然圆的模型在生活中有着广泛运用，下面我们一起来学习和认识圆吧.
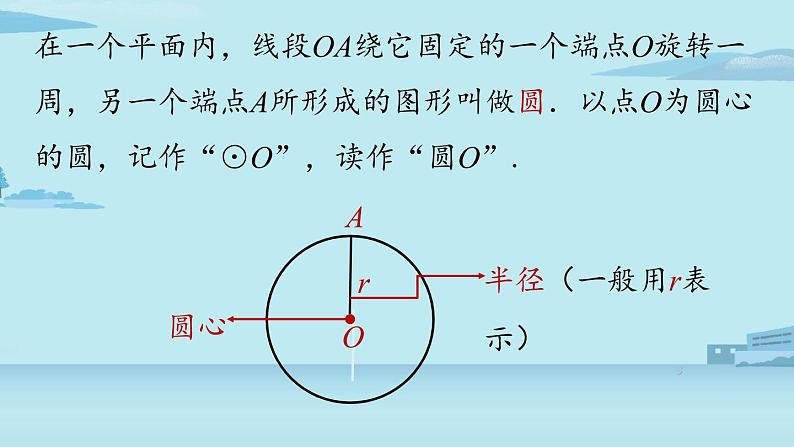
在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做圆．以点O为圆心的圆，记作“⊙O”，读作“圆O”.
圆可以看成是所有到定点（圆心）O的距离等于定长（半径）r的点的集合.
到定点的距离等于定长的点都在同一个圆上吗？
一是圆心，圆心确定圆的位置；
二是半径，半径确定圆的大小．
1.下列条件中，可以确定一个圆的是( )
A.半径为1 cm B.圆心在点O处C.半径是1 cm，且经过点P D.圆心在点O处，且直径是2 cm
2. 矩形ABCD的对角线AC,BD相交于点O.求证：点A,B,C,D在以O为圆心的同一圆上.
证明：∵四边形ABCD是矩形，
∴AO=OC，OB=OD.
∴点A,B,C,D在以点O为圆心，以OA为半径的圆上.
∴OA=OB=OC=OD.
连接圆上任意两点的线段（如图中的AC）叫做弦.
经过圆心的弦（如图中的AB）叫做直径．
注意：直径是弦，是经过圆心的特殊弦，但弦不一定是直径.
圆中最长的弦是什么？为什么？
圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆．
能够重合的两个圆叫做等圆.
在同圆或等圆中，能够互相重合的弧叫做等弧 .
注意：等弧只能出现在同圆或者等圆中.等弧是全等的，而不仅仅是弧的长度相等.
等弧是全等的，必须在同圆或等圆中，而不仅仅是弧的长度相等
1.下列语句正确的有( )①直径是弦；②弦是直径；③半径相等的两个半圆是等弧；④长度相等的两条弧是等弧；⑤半圆是弧，弧不一定是半圆.
A.1个B.2个C.3个D.4个
2.如图所示，在⊙O中，________是直径，________是弦，劣弧有________，优弧有__________．
3.若圆的半径为3，则弦AB的长度的取值范围是__________．
4.如图，点A，B，C在⊙O上，点O在线段AC上，点D在线段AB上，下列说法正确的是(　　)A. 线段AB，AC，CD，OB都是弦B. 与线段OB相等的线段有OA，OC，CDC. 图中的优弧有2条D. AC是弦，AC又是⊙O的直径， 所以弦是直径
弦是圆上任意两点的线段
直径是弦，是经过圆心的特殊弦，但弦不一定是直径
5.如图所示，AB，MN是⊙O中两条互相垂直的直径，点P在弧AM上，且不与点A，M重合，过点P作AB，MN的垂线，垂足分别是D，C.当点P在弧AM上移动时，矩形PCOD的形状、大小随之变化，则PC 2＋PD 2的值(　　)A. 逐渐变大 B. 逐渐变小C. 不变 D. 不能确定
解：如图，连接OP，CD.
∵四边形PCOD是矩形，
∴△CPD为直角三角形.
∵在矩形PCOD中，OP=CD,
∴PC²+PD²=CD².
∴ PC²+PD²=OP².
即PC²+PD²的值始终等于半径的平方.
1.如图所示，若BD,CE都是△ABC的高．求证：B，C，D，E 四点在同一个圆上．
证明：如图，取BC的中点F，连接FE，FD.
∵BD，CE都是△ ABC的高，
∴ △ BCD和△ BCE都是直角三角形，
∴DF，EF分别是Rt △ BCD和Rt △ BCE斜边上的中线，
∴DF＝EF＝BF＝CF，
∴B，C，D，E四点在以点F为圆心，BF的长为半径的圆上．
2.如图过A，C，D三点的圆的圆心为点E，过B，F，E三点的圆的圆心为点D，∠CAE＝63°，则∠CBE＝______°
∴∠ACE=∠CAE=63°，
∴∠AEC=180°-63°×2=54°.
∵DE=DB，∴∠DEB=∠CBE，
∴∠CDE=∠DEB+∠CBE=2∠CBE.
∴∠AEC=∠ECD＋∠CBE=3∠CBE.
∴∠ECD=∠CDE.
要画一个确定的圆，关键是确定圆心和半径
1.下列语句中正确的有( )①相等的圆心角所对的弧相等；②在同圆或等圆中，相等的弦所对的弧相等；③经过圆心的每一条直线都是圆的对称轴.
A.0个B.1个C.2个D.3个
2.如图，菱形ABCD的对角线AC和BD相交于点O，点E，F，G，H分别为边AB，BC，CD，DA的中点，那么点E，F，G，H是否在同一个圆上？请说明理由.
解：点E，F，G，H 在同一个圆上，理由如下：
如图所示，连接OE，OF，OG，OH．
∴AB=BC=CD=DA，OA=OC，OB=OD.
∵四边形ABCD是菱形，