
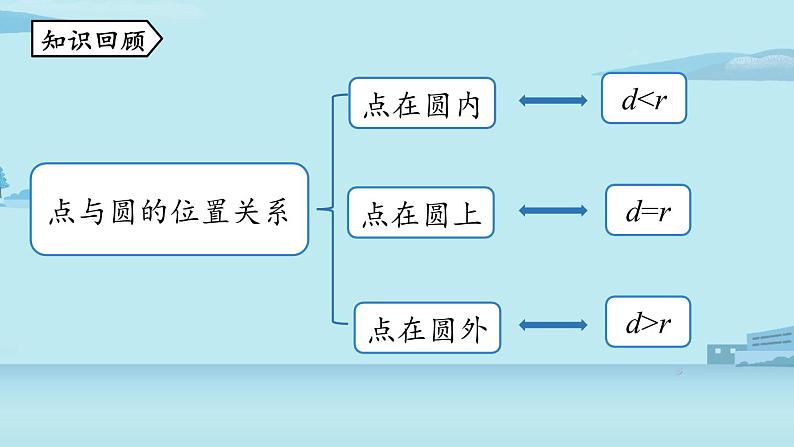


还剩18页未读,
继续阅读
所属成套资源:人教版九年级数学上册精品教学PPT(课件)
成套系列资料,整套一键下载
初中数学人教版九年级上册24.2.2 直线和圆的位置关系完美版ppt课件
展开
这是一份初中数学人教版九年级上册24.2.2 直线和圆的位置关系完美版ppt课件,共26页。PPT课件主要包含了知识回顾,学习目标,课堂导入,知识点,新知探究,位置关系,公共点个数,直线和圆相交,直线和圆相切,直线和圆相离等内容,欢迎下载使用。
1.了解直线和圆的位置关系.
2.理解直线和圆的三种位置关系时,圆心到直线的距离d和圆的半径r之间的数量关系.
3.会从公共点的个数或d和r的数量关系判定直线和圆的位置关系.
如果我们把太阳看作一个圆,把地平线看作一条直线,太阳升起的过程中,太阳和地平线会有几种位置关系?
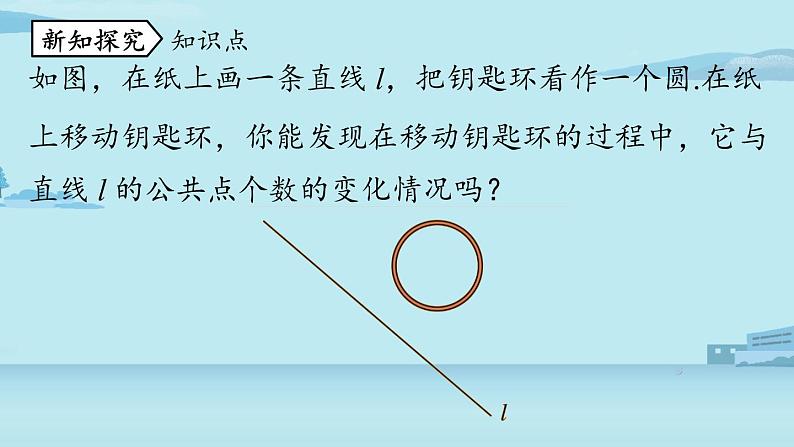
如图,在纸上画一条直线 l,把钥匙环看作一个圆.在纸上移动钥匙环,你能发现在移动钥匙环的过程中,它与直线 l 的公共点个数的变化情况吗?
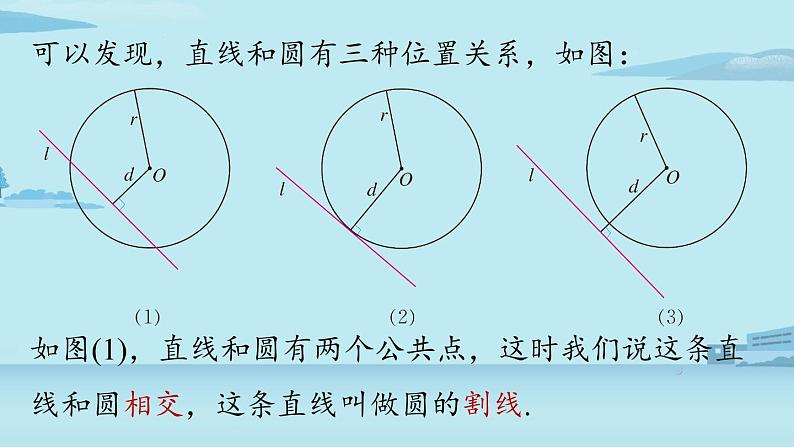
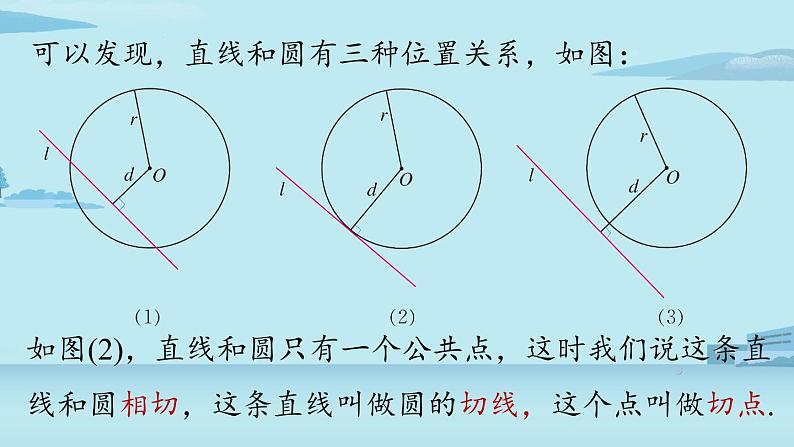
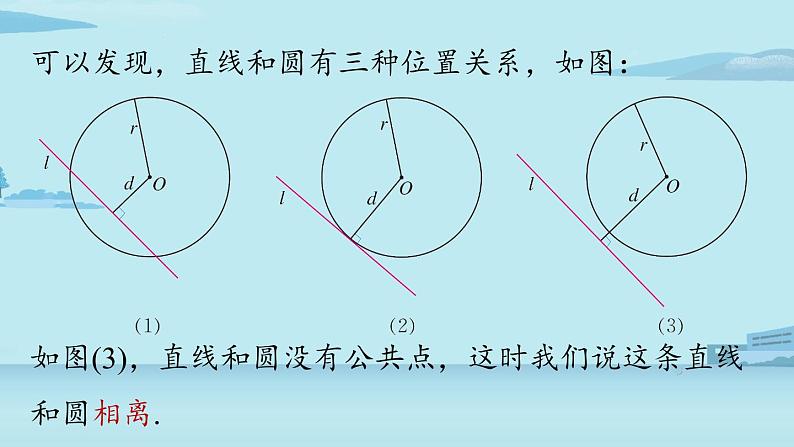
可以发现,直线和圆有三种位置关系,如图:
如图(1),直线和圆有两个公共点,这时我们说这条直线和圆相交,这条直线叫做圆的割线.
如图(2),直线和圆只有一个公共点,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.
如图(3),直线和圆没有公共点,这时我们说这条直线和圆相离.
如何用数量关系来度量这种位置关系呢?
用圆心到直线的距离d与半径r的大小关系来判断直线与圆的位置关系.
1.判断直线和圆的位置关系有两种方法: ①将圆心到直线的距离与圆的半径相比较; ②根据直线与圆的公共点的个数判定.
2.直线与圆相切是一种特殊的位置关系,一个圆有无数条切线,每一条切线与圆都只有一个公共点.
1.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=4 cm,以点C为圆心,2 cm为半径作圆,则⊙C与AB的位置关系是( ) A.相离 B.相切 C.相交 D.相切或相交
解:如图,过点C作CH⊥AB于点H,在Rt△CHB中,易得CH=2 cm,即d=r=2 cm,所以⊙C与AB的位置关系是相切.
分析:通过比较圆心到直线的距离与半径的大小来判断.
已知圆的直径为13 cm,设直线和圆心的距离为d.若d =4.5 cm,则直线与圆 ,直线与圆有 个公共点;(2) 若d =6.5 cm,则直线与圆 ,直线与圆有 个公共点;(3) 若d = 8 cm,则直线与圆 ,直线与圆有 个公共点.
2.在平面直角坐标系中,以点(3,2)为圆心,3为半径的圆,一定( )A.与x轴相切,与y轴相切B.与x轴相切,与y轴相交C.与x轴相交,与y轴相切D.与x轴相交,与y轴相交
1.已知⊙O的半径为5 cm,圆心O到直线 l 的距离为5 cm,则直线 l 与⊙O的位置关系为( )
A.相交B.相切C.相离D.无法确定
2.如图,Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm,判断以点C为圆心,下列 r 为半径的⊙C与AB的位置关系:(1) r =2 cm; (2) r=2.4 cm; (3) r =3 cm.
解:作CD⊥AB于D,如图,
(1) 当 r=2时,CD>r,所以⊙C与AB相离;(2) 当 r=2.4时,CD=r,所以⊙C与AB相切;(3) 当 r=3时,CD<r,所以⊙C与AB相交.
相离:d>r相切:d=r相交:d0个:相离;1个:相切;2个:相交
d>r:相离,d=r:相切,d相离:0个相切:1个相交:2个
1.如果直线上一点与一个圆的圆心的距离等于这个圆的半径,那么这条直线与这个圆的位置关系是( )
A.相交B.相切C.相交或相切D.以上都不正确
解:如果直线上一点与一个圆的圆心的距离等于这个圆的半径,根据垂线段最短,则圆心到直线的距离小于或等于圆的半径,从而直线和圆相交或相切.
2.已知直线 y= kx(k≠0) 经过点(12, -5),将直线向上平移m(m>0)个单位长度,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点) ,试确定m的取值范.
1.了解直线和圆的位置关系.
2.理解直线和圆的三种位置关系时,圆心到直线的距离d和圆的半径r之间的数量关系.
3.会从公共点的个数或d和r的数量关系判定直线和圆的位置关系.
如果我们把太阳看作一个圆,把地平线看作一条直线,太阳升起的过程中,太阳和地平线会有几种位置关系?
如图,在纸上画一条直线 l,把钥匙环看作一个圆.在纸上移动钥匙环,你能发现在移动钥匙环的过程中,它与直线 l 的公共点个数的变化情况吗?
可以发现,直线和圆有三种位置关系,如图:
如图(1),直线和圆有两个公共点,这时我们说这条直线和圆相交,这条直线叫做圆的割线.
如图(2),直线和圆只有一个公共点,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.
如图(3),直线和圆没有公共点,这时我们说这条直线和圆相离.
如何用数量关系来度量这种位置关系呢?
用圆心到直线的距离d与半径r的大小关系来判断直线与圆的位置关系.
1.判断直线和圆的位置关系有两种方法: ①将圆心到直线的距离与圆的半径相比较; ②根据直线与圆的公共点的个数判定.
2.直线与圆相切是一种特殊的位置关系,一个圆有无数条切线,每一条切线与圆都只有一个公共点.
1.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=4 cm,以点C为圆心,2 cm为半径作圆,则⊙C与AB的位置关系是( ) A.相离 B.相切 C.相交 D.相切或相交
解:如图,过点C作CH⊥AB于点H,在Rt△CHB中,易得CH=2 cm,即d=r=2 cm,所以⊙C与AB的位置关系是相切.
分析:通过比较圆心到直线的距离与半径的大小来判断.
已知圆的直径为13 cm,设直线和圆心的距离为d.若d =4.5 cm,则直线与圆 ,直线与圆有 个公共点;(2) 若d =6.5 cm,则直线与圆 ,直线与圆有 个公共点;(3) 若d = 8 cm,则直线与圆 ,直线与圆有 个公共点.
2.在平面直角坐标系中,以点(3,2)为圆心,3为半径的圆,一定( )A.与x轴相切,与y轴相切B.与x轴相切,与y轴相交C.与x轴相交,与y轴相切D.与x轴相交,与y轴相交
1.已知⊙O的半径为5 cm,圆心O到直线 l 的距离为5 cm,则直线 l 与⊙O的位置关系为( )
A.相交B.相切C.相离D.无法确定
2.如图,Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm,判断以点C为圆心,下列 r 为半径的⊙C与AB的位置关系:(1) r =2 cm; (2) r=2.4 cm; (3) r =3 cm.
解:作CD⊥AB于D,如图,
(1) 当 r=2时,CD>r,所以⊙C与AB相离;(2) 当 r=2.4时,CD=r,所以⊙C与AB相切;(3) 当 r=3时,CD<r,所以⊙C与AB相交.
相离:d>r相切:d=r相交:d
d>r:相离,d=r:相切,d
1.如果直线上一点与一个圆的圆心的距离等于这个圆的半径,那么这条直线与这个圆的位置关系是( )
A.相交B.相切C.相交或相切D.以上都不正确
解:如果直线上一点与一个圆的圆心的距离等于这个圆的半径,根据垂线段最短,则圆心到直线的距离小于或等于圆的半径,从而直线和圆相交或相切.
2.已知直线 y= kx(k≠0) 经过点(12, -5),将直线向上平移m(m>0)个单位长度,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点) ,试确定m的取值范.













