



人教版九年级上册24.3 正多边形和圆精品课件ppt
展开中心、半径、边心距、中心角
添加辅助线的方法:连半径,作边心距
会利用等分圆周画圆内接正多边形.
正多边形和圆有什么关系?你能借助圆画一个正多边形吗?
只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.以圆内接正五边形为例进行证明.
证明:如图,得到五边形ABCDE.∵∴AB=BC=CD=DE=EA,∴∠A=∠B. 同理可得∠B=∠C=∠D=∠E.又五边形ABCDE的顶点都在⊙O上,∴五边形ABCDE是⊙O的内接正五边形,⊙O是正五边形ABCDE的外接圆.
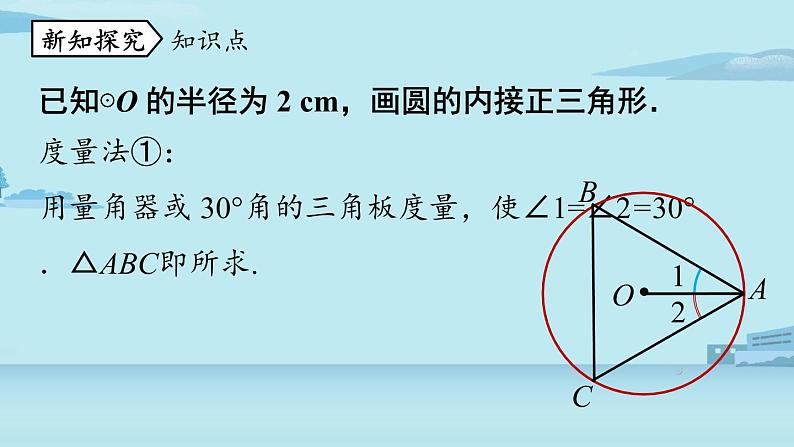
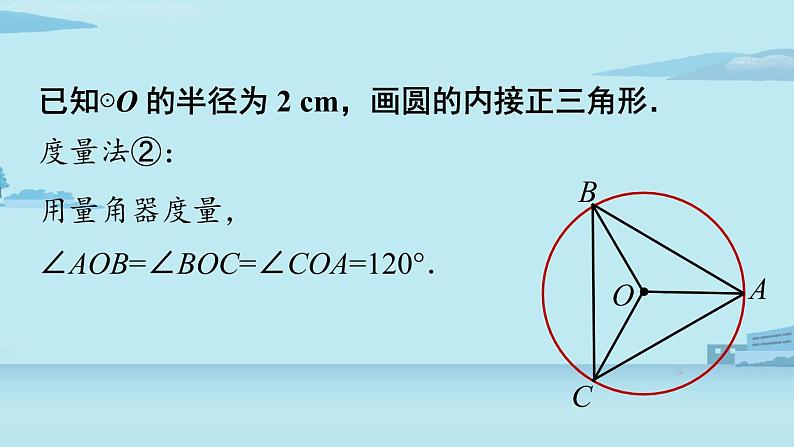
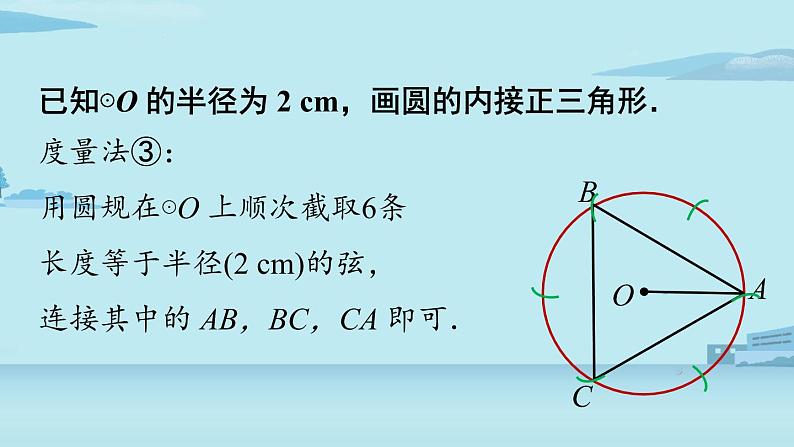
已知⊙O 的半径为 2 cm,画圆的内接正三角形.
度量法①:用量角器或 30°角的三角板度量,使∠1=∠2=30°.△ABC即所求.
度量法②:用量角器度量,∠AOB=∠BOC=∠COA=120°.
度量法③:用圆规在⊙O 上顺次截取6条长度等于半径(2 cm)的弦,连接其中的 AB,BC,CA 即可.
例如,由于正六边形的边长等于半径,所以在半径为R的圆上依次截取等于R的弦,就可以把圆六等分,顺次连接各分点即可得到半径为R的正六边形.
对于一些特殊的正多边形,还可以用圆规和直尺来作图.
再如,用直尺和圆规作两条互相垂直的直径,就可以把圆四等分,从而作出正方形.
次方法简便,且可以画任意正多边形、误差小.
②用尺规等分圆:用尺规作图的方法等分圆周,然后依次连接圆上各分点得到正多边形.
这种方法有局限性,不是任意正多边形都能用此法作图,这种方法从理论上讲是一种准确方法.
用等分圆周的方法画出下列图案.
解:(1)把圆六等分,分别以六等分点A,B,C,D,E,F为圆心,都以OA为半径画弧即可得到图案.(2)把圆五等分,分别以五等分点A,B,C,D,E为圆心,都以AB为半径画弧即可得到图案.
1.画一个半径为2 cm的正五边形,再作出这个正五边形的各条对角线,画出一个五角星.
2.面积相等的正三角形与正六边形的边长之比为 .
3.如图,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEFG…的边AB,BC上的点,且BM=CN,连接OM,ON. (1)图(1)中∠MON的度数是________;(2)图(2)中,∠MON的度数是________,图(3)中∠MON的度数是________;
(3)直接写出∠MON的度数与正n边形的边数n之间的关系式: .
(1)图①中∠MON的度数是________;(2)图②中,∠MON的度数是________,图③中∠MON的度数是________;
(3)直接写出∠MON的度数与正n边形的边数n之间的关系式: .
连接OB,OC,△OMB≌△ONC,∠MON=∠BOC.
此方法可将圆任意n等分,所以用该方法可作出任意正多边形,但边数很大时,容易产生较大的误差.
此方法是一种比较准确的等分圆的方法,但有局限性,不能将圆任意等分.
1.已知⊙O如图所示.(1) 求作⊙O的内接正方形(要求尺规作图,保留作图痕迹,不写作法);(2) 若⊙O的半径为4,求它的内接正方形的边长.
解:(1) 如图所示,正方形ABCD即为所求.(2) ⊙O的半径为4,四边形ABCD是正方形,所以 AC⊥BD,OA=OB=4,所以 AB=
作直径AC的垂直平分线.
2.如图,正五边形ABCDE的对角线AC和BE相交于点M.求证:(1) AC//ED;(2) ME=AE.
3.(2020.绥化中考)如图,正五边形ABCDE内接于⊙O,点P为 上一点(点P与点D,点E不重合),连接PC,PD,DG⊥PC,垂足为G,∠PDG等 于 度.
解:连接OC,OD,如图所示.∵四边形ABCDE是正五边形,∴∠COD=360º÷5=72º,∴∠CPD=36º.∵DG⊥PC, ∴∠PGD=90°,∴∠PDG=90º-∠CPD=90º-36º=54°.
4.(2020•随州中考)设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h,r,R,则下列结论不正确的是( )
A.h=R+r B.R=2r C. D.
解:如图,∵△ABC是等边三角形,∴△ABC的内切圆和外接圆是同心圆,圆心为O.设OE=r,AO=R,AD=h,∴h=R+r,故A正确;
人教版九年级上册第二十四章 圆24.3 正多边形和圆备课ppt课件: 这是一份人教版九年级上册第二十四章 圆24.3 正多边形和圆备课ppt课件,共12页。PPT课件主要包含了复习并导入,例题学习,变式题,能力提升,说一说自己的收获,P8978等内容,欢迎下载使用。
数学九年级上册24.3 正多边形和圆课文ppt课件: 这是一份数学九年级上册24.3 正多边形和圆课文ppt课件,共27页。PPT课件主要包含了学习目标,新课导入,圆内接四边形的性质,新课讲解,正三角形,正方形,什么叫做正多边形,知识点,正n边形与圆的关系,弧相等等内容,欢迎下载使用。
数学九年级上册24.1.1 圆习题课件ppt: 这是一份数学九年级上册24.1.1 圆习题课件ppt,共30页。PPT课件主要包含了任意两点,两点间的部分等内容,欢迎下载使用。













