



数学第二十四章 圆综合与测试获奖课件ppt
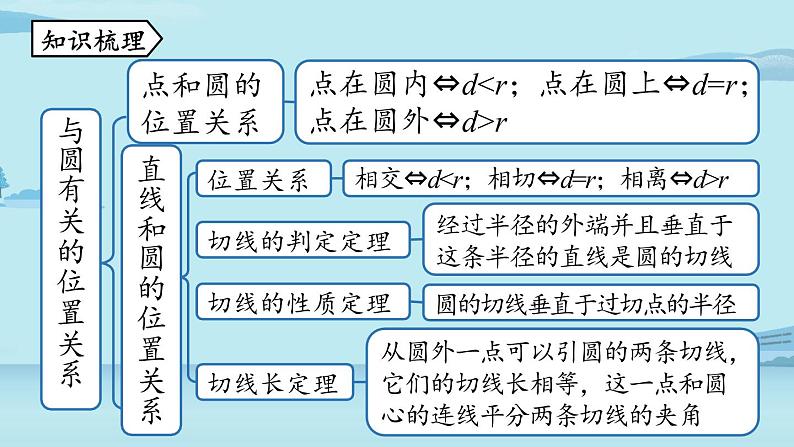
展开点在圆内⇔d
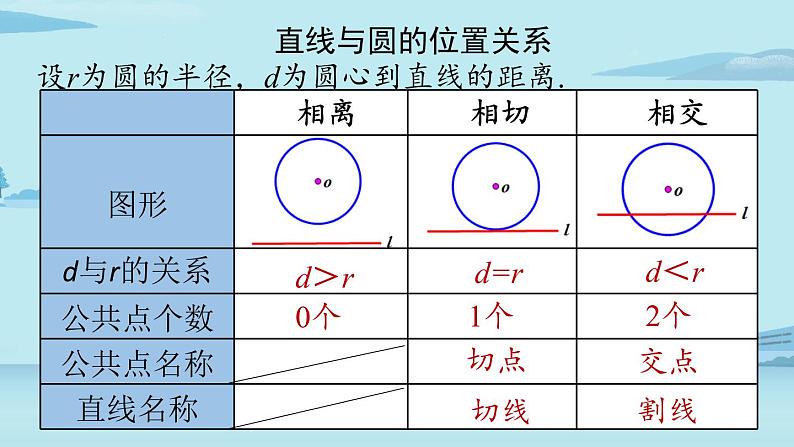
相交⇔d
经过半径的外端并且垂直于这条半径的直线是圆的切线
圆的切线垂直于过切点的半径
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角
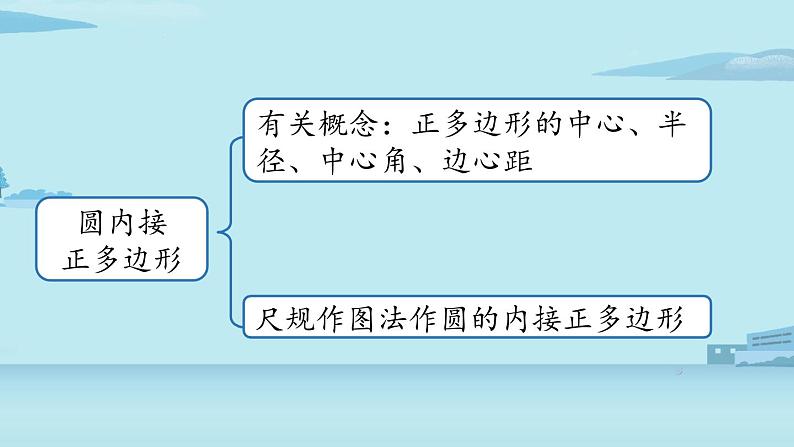
有关概念:正多边形的中心、半径、中心角、边心距
尺规作图法作圆的内接正多边形
圆锥的侧面积和全面积公式
判断点与圆的位置关系可由点到圆心的距离d与圆的半径r比较得到.设☉O的半径是r,点P到圆心的距离为d,则有
注意:点与圆的位置关系可以转化为点到圆心的距离与半径之间的关系;反过来,也可以通过这种数量关系判断点与圆的位置关系.
例:已知⊙O的半径为4 cm,A为线段OP的中点,当OP=7 cm时,点A与⊙O的位置关系是( ) A.点A在⊙O内 B.点A在⊙O上 C.点A在⊙O外 D.不能确定
解:∵ OP=7 cm,A为OP的中点,∴OA=3.5cm.∵ 3.5cm<4 cm,∴点A在⊙O内.
设r为圆的半径,d为圆心到直线的距离.
例:设⊙O的半径为2,圆心O到直线l的距离OP=m,且m使得关于x的方程 有实数根,则直线l与⊙O的位置关系是( )A.相离或相切 B.相切或相交C.相离或相交 D.无法确定
1.判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
2.性质定理:圆的切线垂直于过切点的半径.
∵l⊥OA于A,OA是半径∴l是⊙O的切线.
∵l与⊙O相切于A,∴l⊥OA.
例: 如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.(1)求证:AC是⊙O的切线;(2)若OB=10,CD=8,求BE的长.
(1)证明:连接OD,如图所示.∵BD为∠ABC的平分线,∴∠1=∠2.又∵OB,OD均为⊙O的半径,∴OB=OD,∴∠1=∠3,∴∠2=∠3,∴OD∥BC,∴∠ODA=∠C=90°,即OD⊥AC.又∵OD是⊙O的半径,∴AC是⊙O的切线.
(1)求证:AC是⊙O的切线;
(2)解:过圆心O作OF⊥BE于点F,如图所示.在Rt△BOF中,OB=10,OF=CD=8,根据勾股定理可得OB2=BF2+OF2,即102=BF2+82,解得BF=6.由垂径定理可知F为BE的中点,∴BE=2BF=12.
(2)若OB=10,CD=8,求BE的长.
3.切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
∵PA,PB分别与⊙O相切于A,B,∴PA=PB,∠APO=∠BPO.
例1: 如图,AC是⊙O的直径,PA,PB分别与⊙O相切于A,B,若∠BAC=25°,则∠P=______°.
例2: 如图,直线AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,OB=6 cm,OC=8 cm.求:(1)∠BOC的度数;(2)BE+CG的长;(3)⊙O的半径.
解: (1) 连接OF,根据切线长定理,得BE=BF, CF=CG,∠OBF=∠OBE, ∠OCF= ∠OCG.∵AB∥CD, ∴ ∠ABC+ ∠BCD = 180°,∴ ∠OBF + ∠OCF=90°, ∴∠BOC=90°.
(1)∠BOC的度数;
(2)BE+CG的长;(3)⊙O的半径.
弓形的面积=扇形的面积±三角形的面积
(1)判定直线CD与⊙O的位置关系,并说明理由;
解: (1) CD是⊙O的切线. 理由如下:连接OC.∵ EC=BC ,∴∠CAD=∠BAC.∵OA=OC,∴∠BAC=∠ACO,∴∠CAD=∠ACO,∴AD∥OC. ∵AD⊥CD,∴OC⊥CD,∴CD是⊙O的切线.
(2)若AB=4,CD= ,求图中阴影部分的面积.
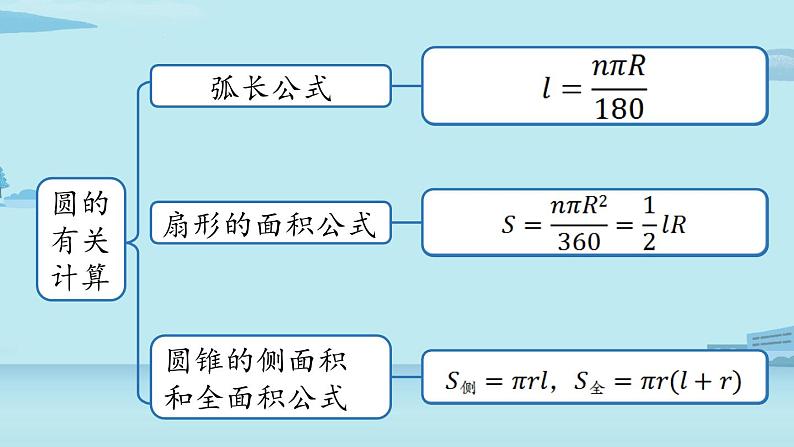
3.圆锥的侧面积为πrl.
4.圆锥的全面积为πrl+πr2.
1.圆锥的侧面展开图是一个扇形.2.如果圆锥母线长为l,底面圆的半径为r,那么这个扇形的半径为l,扇形的弧长为2πr.
例:有一块圆心角为300°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝处忽略不计),若圆锥的底面圆的直径是80 cm,则这块扇形铁皮的半径是( )A.24 cm B.48 cm C.96 cm D.192 cm
1.中心:正多边形外接圆和内切圆有公共的圆心,称其为正多边形的中心.
2.半径:外接圆的半径叫做正多边形的半径.
3.边心距:中心到正多边形一边的距离叫做正多边形的边心距.
4.中心角:正多边形每一条边所对的外接圆的圆心角都相等,叫做正多边形的中心角.
例: (2020·南京中考)如图,在边长为2cm 的正六边形ABCDEF中,点P在BC上,则△PEF的面积为 cm2.
解:连接BF, BE, 过A作AT⊥BF于T, ∵ABCDEF是正六边形, ∴CB∥EF,AB=AF,∠BAF=120°,∴S△PEF=S△BEF.
1.如图, O为正方形对角线上一点,以点O 为圆心,OA长为半径的☉O与BC相切于点M.(1) 求证:CD与☉O相切.(2) 若正方形ABCD的边长为1,求☉O的半径.
(1) 证明:过点O作ON⊥CD于N.连接OM. ∵BC与☉O相切于点M, ∴ ∠OMC=90 °, ∵四边形ABCD是正方形,点O在AC上.∴AC是∠BCD的平分线,∴ON=OM,∴CD与☉O相切.
2.如图,PA,PB是⊙O的切线,A,B为切点,过AB 上的一点C作⊙O的切线,交PA于D,交PB于E.(1) 若∠P=70°,求∠DOE的度数;(2) 若PA=4 cm,求△PDE的周长.
解:(2)∵⊙O分别切PA,PB,DE于A,B,C,∴AD=CD,BE=CE.∴ △PDE的周长=PD+PE+DE=PD +AD +PE +BE=2PA=8(cm).
2.如图,PA,PB是⊙O的切线,A,B为切点,过 AB上的一点C作⊙O的切线,交PA于D,交PB于E.(1) 若∠P=70°,求∠DOE的度数;(2) 若PA=4 cm,求△PDE的周长.
3.如图,四边形OABC为菱形,点B,C在以点O为圆心的圆上,OA=1,∠AOC=120°,∠1=∠2,求扇形OEF的面积.
4.如图所示,在正方形ABCD内有一条折线段,其中AE⊥EF,EF⊥FC,已知AE=6,EF=8,FC=10,求图中阴影部分的面积.
解:将线段FC平移到直线AE上,同理平移EF. 连接AC,如图所示.
根据平移的方法可知,四边形EFCC'是矩形.
∴ AC'=AE+EC'=AE+FC=16,CC'=EF=8.
1.☉O的半径为R,圆心到点A的距离为d,且R,d分别是方程x2-6x+8=0的两根,则点A与☉O的位置关系是( )A. 点A在☉O内部 B. 点A在☉O上C. 点A在☉O外部 D. 点A不在☉O上
解:解方程 x2-6x+8=0的两根,得R=2,d=4,或R=4,d=2,当R=2,d=4时,点A在⊙O外部;当R=4,d=2时,点A在⊙O内部;综上所述,点A不在⊙O上.
2.如图,直线AB,CD相交于点O, ∠AOD=30 °,半径为1 cm的☉P的圆心在射线OA上,且与点O的距离为6 cm,如果☉P以1 cm/s的速度沿由A向B的方向移动,那么 秒钟后☉P与直线CD相切.
解:当⊙P在射线OA上,设⊙P与CD相切于点E,P移动到P1时,连接P1E.∵⊙P与直线CD相切,∴∠OEP1=90°,∵在Rt△OP1E中,P1E=1cm,∠AOD=30°,∴OP1=2P1E=2cm,则PP1=OP-OP1=6-2=4(cm).
∵⊙P以1 cm/s的速度沿由A向B的方向移动,∴⊙P移动4秒时与直线CD相切.当⊙P移动到直线CD的右侧时,PP2=4+4=8(cm).∴⊙P移动8秒时与直线CD相切.综上,⊙P移动4秒或8秒时,与直线CD相切.
3.一条弧所对的圆心角为135 °,弧长等于半径为5 cm 的圆的周长的3倍,则这条弧的半径为 .
4.若一个正六边形的周长为24,则该正六边形的面积为______.
5.如图,已知C,D是以AB为直径的半圆周上的两点,O是圆心,半径OA=2,∠COD=120°,则图中阴影部分的面积等于_____.
6.如图,正六边形ABCDEF内接于半径为5的⊙O,四边形EFGH是正方形.(1) 求正方形EFGH的面积;(2) 连接OF,OG,求∠OGF的度数.
解:(1) ∵正六边形的边长与其外接圆半径相等,∴EF=5.∵四边形EFGH是正方形,∴FG=EF=5,∴正方形EFGH的面积是25.
初中数学人教版九年级上册第二十五章 概率初步综合与测试完整版课件ppt: 这是一份初中数学人教版九年级上册第二十五章 概率初步综合与测试完整版课件ppt,共29页。PPT课件主要包含了直接列举法,列表法,画树状图法,用列举法求概率,用频率估计概率,知识梳理,第一枚,第二枚,跟踪训练,能力提升等内容,欢迎下载使用。
初中数学人教版九年级上册第二十五章 概率初步综合与测试优质ppt课件: 这是一份初中数学人教版九年级上册第二十五章 概率初步综合与测试优质ppt课件,共21页。PPT课件主要包含了知识梳理,随机事件,重点剖析,概率的概念,不可能发生,必然发生,概率的值,概率的取值范围,跟踪练习,能力提升等内容,欢迎下载使用。
2021学年第二十四章 圆综合与测试公开课课件ppt: 这是一份2021学年第二十四章 圆综合与测试公开课课件ppt,共21页。PPT课件主要包含了圆的有关概念,确定圆的要素,直径是最长的弦,确定圆的位置,确定圆的大小,知识梳理,圆的基本性质和定理,圆的对称性,垂径定理及其推论,弧弦的关系等内容,欢迎下载使用。













