

2021年陕西省西安市中考数学一模试题(word版 含答案)
展开2021年陕西省西安市中考数学一模试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.的倒数是( )
A. B. C. D.2021
2.如图所示的几何体,其俯视图是( )
A. B. C. D.
3.截止北京时间10月5日22点前,全球新冠肺炎累计确诊病例已超过35000000例,这个数用科学记数法表示为( )
A.0.35×108 B.3.5×107 C.3.5×108 D.0.35×107
4.如图,将一个直角尺的顶点放在尺子的一边,若∠1=24°,那么∠2的度数是( )
A.24° B.56° C.66° D.76°
5.下列运算正确的是( )
A.3a2•2a3=6a5 B.(﹣a2)3=a6
C.(a﹣b)2=a2﹣b2 D.x2+x2=x4
6.在平面直角坐标系中,若一个正比例函数的图象经过A(m,2),点B(5,n)两点,则m,n一定满足的关系式为( )
A.m﹣n=3 B. C. D.mn=10
7.如图,在等边△ABC中,作点C关于直线AB的对称点P,过点P作PQ⊥BC,交CB的延长线于点Q,BQ=5,则AC的长为( )
A.5 B.5 C.10 D.15
8.如图,在矩形ABCD中,AB=4,FG=,AE平分∠BAD交BC于点E.点F,G分别是AD,AE的中点,则BC的长为( )
A.3 B.5 C.7 D.8
9.如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,若水面下降2.5m,那么水面宽度为( )m.
A.3 B.6 C.8 D.9
10.若直线y=n截抛物线y=x2+bx+c所得线段AB=4,且该抛物线与x轴只有一个交点,则n的值为( )
A.﹣1 B.2 C.25 D.4
二、填空题
11.把多项式分解因式的结果是_____________.
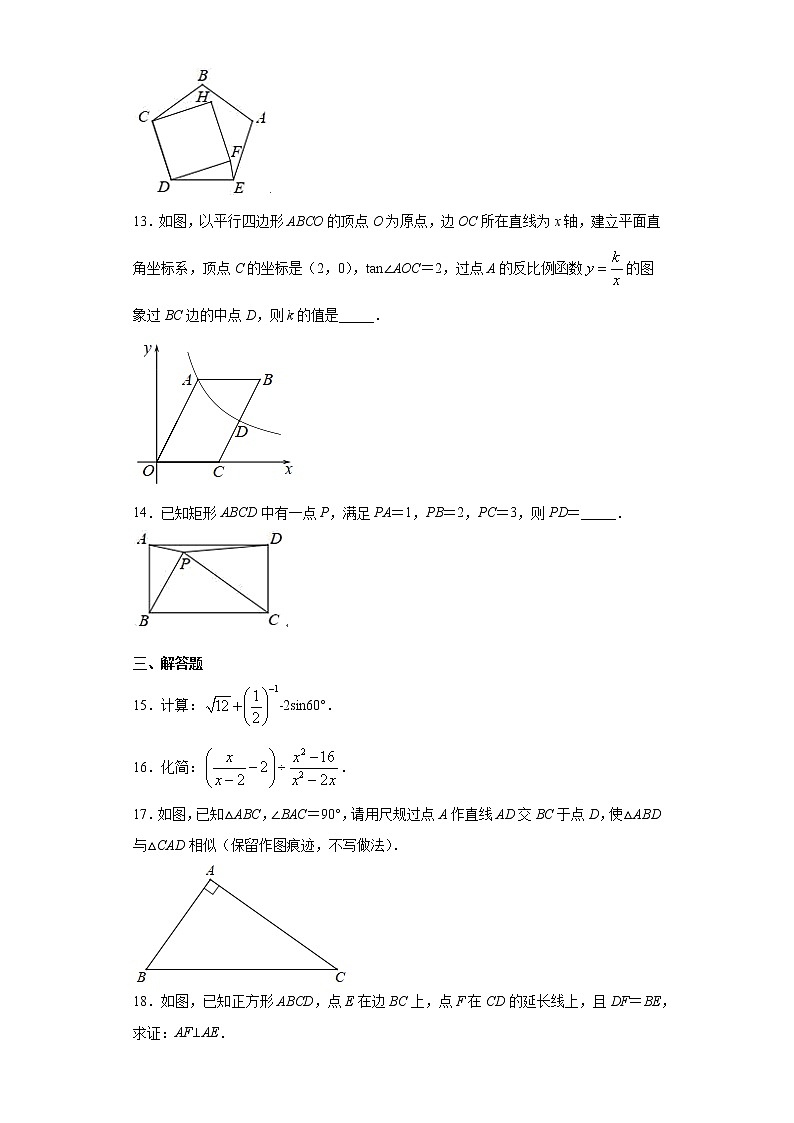
12.如图,以正五边形ABCDE的边CD为边作正方形CDFH,使点F,H在其内部,连接FE,则∠DFE=_____.
13.如图,以平行四边形ABCO的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点C的坐标是(2,0),tan∠AOC=2,过点A的反比例函数的图象过BC边的中点D,则k的值是_____.
14.已知矩形ABCD中有一点P,满足PA=1,PB=2,PC=3,则PD=_____.
三、解答题
15.计算:﹣2sin60°.
16.化简:.
17.如图,已知△ABC,∠BAC=90°,请用尺规过点A作直线AD交BC于点D,使△ABD与△CAD相似(保留作图痕迹,不写做法).
18.如图,已知正方形ABCD,点E在边BC上,点F在CD的延长线上,且DF=BE,求证:AF⊥AE.
19.某中学数学兴趣小组为了了解参加数学学科节学生的年龄情况,随机抽取了其中部分学生的年龄,经过数据整理,绘制出如下不完整的统计图,依据相关信息解答以下问题:
(1)写出被抽取的学生人数 ,并补全条形统计图.
(2)被抽取的学生的年龄的众数是 岁,中位数是 岁.
(3)若共有600名学生参加了本次数学学科节活动,请估计活动中年龄在15岁及以上的学生人数.
20.如图,AB,CD为两栋建筑物,从建物CD顶端C处测得建筑物AB顶端A的俯角为22°,BM为此时阳光下建筑物AB在地面上的影子,且获知此时刻长为1米的标杆影长为1.1米,建筑物AB顶端A在地面上的影子M与墙角D的距离为10m(B、M、D在同一直线上),建筑物CD的高28米,求建筑物AB的高度;(结果保留一位小数)参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
21.早晨六点,小张开车去距出发地路程为150km的A地,车匀速行驶,在行驶过程中,前方发生交通事故,被堵了一些时间,事故处理后,小张提高速度,继续匀速前进;整个过程中小张出发后行驶的路程y(km)与其行驶时间x(h)的函数关系如图所示,根据图象回答下列问题:
(1)求小张提高速度后y与x的函数表达式;
(2)小张能否在早晨九点之前赶到A地?请说明理由.
22.周天,苗苗准备了5盒外包装完全相同的橡皮泥,准备和好朋友一起做手工,其中2盒红色,2盒黄色,1盒绿色.
(1)若苗苗随机打开一盒橡皮泥,恰巧是红色的概率是 ;
(2)若苗苗同时打开两盒橡皮泥,请你计算两盒颜色恰好相同的概率(请用画树状图或列表的方法求解)
23.已知二次函数y=x2+bx+c(a≠0)自变量x的值和它对应的函数值y如表所示:
x
……
0
1
2
3
4
……
y
……
3
0
﹣1
0
m
……
(1)请写出关于该二次函数图象的相关信息:
抛物线解析式为 ;抛物线开口向 (填“上”或“下”);顶点坐标为 ;m的值为 .
(2)设该二次函数图象与x轴的左交点为B,它的顶点为A,该图象上点C的横坐标为4,求△ABC的面积.
24.如图,已知直线y=x﹣4与坐标轴分别交于点B、点C,二次函数y=﹣x2+2x的图像经过点C.
(1)求直线与抛物线的另一个交点A的坐标及线段AB的长;
(2)若点D在x轴的正半轴上,是否存在以点D,C,B构成的三角形与△OAB相似?若存在,求出点D的坐标;若不存在,请说明理由.
25.(1)如图1,在四边形ABCD中,已知ADBC,点M是CD的中点,连接AM并延长交BC的延长线于点E,若=10,那么= .
(2)如图2,已知,锐角∠AOB内有一点M,过点M作直线l分别交OA,OB于点P、Q,将直线l绕点M旋转时,发现:当点M恰好是PQ中点时,最小,请证明这个结论.
(3)如图3,已知在直角坐标系中,OA是第一象限的角分线,∠MOx=30°,且OM=3,过点M作直线l交OA于点P,交x轴正半轴于点Q,求的最小值及此时直线l的表达式.
参考答案
1.D
【分析】
直接利用倒数的定义分析得出答案.
【详解】
解:的倒数为:2021.
故选:D.
【点睛】
此题主要考查了倒数,正确把握倒数定义是解题关键.
2.A
【分析】
根据俯视图的定义即可求解.
【详解】
由图形可知,这个几何体的俯视图为
故选A.
【点睛】
此题主要考查俯视图的判断,解题的关键是熟知俯视图的定义.
3.B
【分析】
根据科学计数法的要求先确定a的值,再确定10的指数.
【详解】
因为35000000=3.5×107,
故选:B.
【点睛】
本题考查了绝对值大于1的数的科学计数法,记住科学计数法中a的取值范围,避免出错.
4.C
【分析】
先根据两角互余的性质求出的度数,再由平行线的性质即可得出结论.
【详解】
解:如图:
直尺的两边互相平行
故选C.
【点睛】
本题考查了平行线的性质,熟练掌握两直线平行,同位角相等是解题的关键.
5.A
【分析】
根据单项式乘单项式、幂的乘方、完全平方公式及合并同类项逐一计算可得.
【详解】
解:A.,此选项正确;
B.,此选项错误;
C. ,此选项错误;
D. ,此选项错误.
故选A.
【点睛】
本题主要考查单项式乘单项式、幂的乘方、完全平方公式及合并同类项,熟练掌握运算法则是解题的关键.
6.D
【分析】
设正比例函数解析式为y=kx(k≠0),再把A、B点的坐标代入得到mk=2,5k=n,然后消去k得到m、n的关系式.
【详解】
解:设正比例函数解析式为y=kx(k≠0),
把A(m,2),点B(5,n)代入得mk=2,5k=n,
可得,, 代入mk=2得,m•=2,
所以mn=10.
故选:D.
【点睛】
本题考查了待定系数法求正比例函数解析式:先设出正比例函数的解析式为y=kx,然后把一组对应值代入求出k即可.
7.C
【分析】
设PC与AB的交点为D,在等边△ABC中,AB=AC,∠A=∠ABC=∠ACB=60°,由点C关于直线AB的对称点P,可得CD平分∠ACB,由PQ⊥BC,可得∠Q=90°,设BC=x,利用三角函数可求CD= ,PC=,再利用三角函数列方程QC=PCcos30°即5+x=,解之即可.
【详解】
解:设PC与AB的交点为D,
在等边△ABC中,AB=AC,∠A=∠ABC=∠ACB=60°,
∵点C关于直线AB的对称点P,
∴PC⊥AB,PD=CD,
∵CD⊥AB,△ABC为等边三角形,
∴CD平分∠ACB,
∴∠DCB=
∵PQ⊥BC,
∴∠Q=90°,
设BC=x,
∴CD=BCcos30°=,
∴PC=2CD=,
∴QC=PCcos30°即5+x=,
解得:x=10.
故选择:C.
【点睛】
本题考查等边三角形选择,轴对称性质,锐角三角函数,掌握等边三角形选择,轴对称性质,锐角三角函数,利用锐角三角函数构造方程是解题关键.
8.C
【分析】
连接DE,由三角形中位线定理求出DE,再根据勾股定理求出CE,角平分线的性质得出△ABE是等腰有直角三角形,求出BE,从而求出BC.
【详解】
解:连接DE,
∵FG=且F、G分别为AD、AE中点,
∴DE=2FG=5,
∵四边形ABCD为矩形,
∴CD=AB=4,
在△CDE中,CE==3,
∵AE平分∠BAD,四边形ABCD为矩形,
∴∠BAD=∠ABE=90°,
∴∠BAE=∠BAD=45°,
在△ABE中,∠AEB=90°﹣∠AEB=45°,
∴∠BAE=∠AEB=45°,
△ABE为等腰直角三角形,
∴BE=AB=4,
又∵CE=3,
∴BC=BE+CE=4+3=7.
故选:C.
【点睛】
本题考查了矩形的性质,勾股定理,等腰直角三角形的判定与性质,三角形中位线的定理等知识;熟练掌握矩形的性质和三角形中位线定理,求出DE的长度是解题的关键.
9.B
【分析】
根据已知确定平面直角坐标系,进而求出二次函数解析式,再通过把y=﹣2.5代入抛物线解析式得出水面宽度,即可得出答案.
【详解】
解:建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,
抛物线以y轴为对称轴,且经过A,B两点,OA和OB可求出为AB的一半2米,抛物线顶点C坐标为(0,2),
设顶点式y=ax2+2,把A点坐标(﹣2,0)代入得a=﹣0.5,
∴抛物线解析式为y=﹣0.5x2+2,
当水面下降2.5米,通过抛物线在图上的观察可转化为:
当y=﹣2.5时,对应的抛物线上两点之间的距离,也就是直线y=﹣2.5与抛物线相交的两点之间的距离,
可以通过把y=﹣2.5代入抛物线解析式得出:
﹣2.5=﹣0.5x2+2,
解得:x=±3,
∴水面宽度为3﹣(﹣3)=6(m).
故选:B.
【点睛】
本题主要考查了二次函数的应用.根据已知建立坐标系从而得出二次函数解析式是解决问题的关键,学会把实际问题转化为二次函数,利用二次函数的性质解决问题.
10.D
【分析】
由抛物线与x轴只有一个交点,得出b2﹣4c=0,设A、B的交点的横坐标为x1、x2,则x1+x2=﹣b,x1x2=c﹣n,由AB=4,即可得出(x1﹣x2)2=(x1+x2)2﹣4x1x2=16,即可得出4n=16,解得n=4.
【详解】
解:∵抛物线与x轴只有一个交点,
∴b2﹣4c=0,
设A、B的交点的横坐标为x1、x2,
∴x1、x2是方程x2+bx+c=n的两个根,
∴x1+x2=﹣b,x1x2=c﹣n,
∵AB=4,
∴|x1﹣x2|=4,
∴(x1﹣x2)2=(x1+x2)2﹣4x1x2=16,
∴(﹣b)2﹣4(c﹣n)=16,即b2﹣4c+4n=16,
∴4n=16,
∴n=4,
故选:D.
【点睛】
本题考查了抛物线与x轴的交点,二次函数与方程的关系,根与系数的关系,根据题意得出(﹣b)2﹣4(c﹣n)=16,即b2﹣4c+4n=16是解题的关键.
11.3a(x+2)(x-2)
【分析】
先提取公因式3a,再根据平方差公式分解即可.
【详解】
=3a(x+2)(x-2),
故答案为:3a(x+2)(x-2).
【点睛】
此题考查因式分解的方法:提公因式法、公式法(平方差公式与完全平方公式),根据多项式的特点选择恰当的因式分解的方法是解题的关键.
12.81°
【分析】
根据正多边形的性质以及内角和求解即可.
【详解】
由正多边形的内角和公式可得:
正五边形ABCDE的内角和为,
∴,
∵四边形CDFH是以CD为边的正方形,
∴,,
∴为等腰三角形,
∴,
故答案为:81°.
【点睛】
本题考查正多边形的性质,理解基本性质是解题关键.
13.
【分析】
作AM⊥x轴于M,DN⊥x轴于N,设A(a,2a),解直角三角形表示出A、D的坐标,根据反比例函数图象上点的坐标特征得到k=a•2a=(2+)•a,解得a=,进而即可求得k的值.
【详解】
解:∵四边形ABCO是平行四边形,
∴OA∥BC,OA=BC,
∴∠DCN=∠AOC,
作AM⊥x轴于M,DN⊥x轴于N,
∵tan∠AOC=2,
∴=2,=2,
∴设A(a,2a),
∴OM=a,AM=2a,,
∵D是BC的中点,,
∴DN=a,CN=a,
∵顶点C的坐标是(2,0),
∴ON=2+a,
∴D(2+,a),
∴a•2a=(2+)•a,
解得a=或a=0(舍去),
∴k=a•2a=,
故答案为.
【点睛】
此题是反比例函数综合题,主要考查了待定系数法,平行四边形的性质以及解直角三角形,解本题的关键是求出a的值.
14.
【分析】
由ABCD是矩形,过P作GHBC交AB、CD于点G、H,过P作EFAB交AD、BC于点E、F,在所形成的直角三角形中,由勾股定理得出AP2+CP2=BP2+DP2,从而求出DP.
【详解】
解:过点P作GHBC交AB、CD于点G、H,过点P作EFAB交AD、BC于点E、F,
设AE=BF=c,AG=DH=a,GB=HC=b,ED=FC=d
,,,
PA=1,PB=2,PC=3,
即
(负值已舍去)
故答案为:.
【点睛】
本题考查了四边形的综合题,矩形的性质,勾股定理,关键是利用勾股定理列方程组.
15.
【分析】
先化简二次根式、负指数、特殊角三角函数值,再进行计算即可.
【详解】
解:﹣2sin60°,
=,
=
=.
【点睛】
本题考查了实数的运算,包括二次根式、负指数、三角函数等,解题关键是熟记三角函数值,准确运用相关知识进行计算.
16.
【分析】
根据分式运算的顺序和法则进行计算即可.
【详解】
解:,
=
=
=
=.
【点睛】
本题考查了分式的运算,解题关键是熟练运用分式运算法则进行准确计算.
17.答案见解析
【分析】
过点A作AD垂直BC于D,直线AD即为所求直线;在△ABD与△CAD中,有 再证明,从而可得△ABD∽△CAD.
【详解】
解:如图,
AD即为所求直线.
【点睛】
此题主要考查作图法和相似三角形变换,解题的关键在于理解题意,灵活运用所学知识解决问题.
18.见解析
【分析】
根据正方形的性质得到∠B=∠ADF=90°,AD=AB,求出∠ADF,根据SAS即可推出答案,再利用全等三角形的性质解答即可.
【详解】
证明:由正方形ABCD,得 AB=AD,∠B=∠ADF=∠BAD=90°.
在△ABE和△ADF中,
∴△ABE≌△ADF(SAS).
∴∠BAE=∠FAD,AE=AF.
∴∠BAD=∠BAE+∠EAD=∠FAD+∠EAD=90°.
即∠EAF=90°.
∴AF⊥AE.
【点睛】
本题主要考查对正方形的性质,全等三角形的性质和判定,垂直的判定等知识点的理解和掌握.关键在于利用SAS判定全等.
19.(1)50,图见解析;(2)15岁,14岁;(3)240人
【分析】
(1)根据12岁的人数和所占的百分比,可以计算出本次被抽查的学生人数,然后即可计算出户14岁和16岁的人数,从而可以将条形统计图补充完整;
(2)根据条形统计图中的数据,可以得到被抽取的学生的年龄的众数和中位数;
(3)根据统计图中的数据,可以计算出活动中年龄在15岁及以上的学生人数.
【详解】
解:(1)被抽取的学生人数:6÷12%=50(人),
故答案为:50,
14岁的学生有:50×28%=14(人),
16岁的学生有50﹣6﹣10﹣14﹣18=2(人),
补全的条形统计图如图所示;
(2)由条形统计图可知,
被抽取的学生的年龄15岁最多,故众数是15岁,从小到大排列后,第25、26个数据都是14岁,所以中位数是14岁,
故答案为:15,14;
(3)600×=240(人),
即估计活动中年龄在15岁及以上的学生有240人.
【点睛】
本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
20.16.7米
【分析】
过点A作AN⊥CD于点N,则四边形ABDN是矩形,设AB=x,则DN=x,根据此时刻长为1米的标杆影长为1.1米,可得AB:BM=1:1.1,所以BM=1.1x(米),可得AN=BD=BM+MD=(1.1x+10)米,CN=CD﹣DN=(28﹣x)米,根据锐角三角函数即可求出x的值.
【详解】
解:如图,过点A作AN⊥CD于点N,
则四边形ABDN是矩形,
∴AB=DN,AN=BD,
设AB=x,则DN=x,
∵此时刻长为1米的标杆影长为1.1米,
∴AB:BM=1:1.1,
∴BM=1.1x(米),
∴AN=BD=BM+MD=(1.1x+10)米,
CN=CD﹣DN=(28﹣x)米,
在Rt△ACN中,
tan∠CAN=,
∴≈0.40,
解得x≈16.7,
∴AB≈16.7(米).
答:建筑物AB的高度约为16.7米.
【点睛】
此题考查了解直角三角形应用﹣仰角俯角问题,平行投影,熟练掌握仰角俯角是解本题的关键.
21.(1)小张提速后y与x的函数表达式为y=60x﹣40;(2)小张不能在九点前赶到A地,理由见解答.
【分析】
(1)根据函数图象中的数据,可以得到小张提高速度后y与x的函数表达式;
(2)将y=150代入(1)中的函数解析式,求出对应的x的值,然后即可得到小张能否在九点之前赶到A地.
【详解】
解:(1)由图可知,
设小张提速后y与x的函数表达式为y=kx+b(k≠0),把(1.5,50),(2,80)代入得,
∴,
解得:,
即小张提速后y与x的函数表达式为y=60x﹣40;
(2)小张不能在九点前赶到A地,
理由:当y=150时,
150=60x﹣40,
解得,x=,
∵>9﹣6,
∴小张不能在九点前赶到某地.
【点睛】
本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.
22.(1);(2)
【分析】
(1)利用概率公式求解即可.
(2)列表得出所以等可能结果,从中找出符合条件的结果数,再根据概率公式求解即可.
【详解】
解:(1)若苗苗随机打开一盒橡皮泥,恰巧是红色的概率是;
(2)列表如下:
由表知,共有20中等可能结果,其中两盒颜色恰好相同的有4种结果,
∴两盒颜色恰好相同的概率为=.
【点睛】
本题考查了根据概率公式求概率,用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所以可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.
23.(1),上,,3;(2)3
【分析】
(1)根据表格中的数据和二次函数的性质,可以得到该二次函数图象的开口方向、对称轴、顶点坐标和m的值;
(2)根据表格中的数据和题意,可以写出点B,点A,点C的坐标,再求出直线AC和x轴的交点,即可得到△ABC的面积.
【详解】
解:(1)由表格可知,x=1和x=3时的函数值相同,都是0,
∴对称轴为直线x==2,
∴当x=4和x=0时的函数值相等,则m=3,顶点为(2,-1),
设抛物线解析式为,
把(0,3)代入得,3=4a-1,
则a=1,
∴抛物线解析式为,
即该二次函数图象的开口方向向上,
故答案为,上,(2,-1),3;
(2)由题意可得,
点B的坐标为(1,0),点A的坐标为(2,-1),点C的坐标为(4,3),
设直线AC的函数解析式为y=kx+b,
∴
解得,
∴直线AC的函数解析式为y=2x-5,
当y=0时,0=2x-5,
解得x=2.5,
则直线AC与x轴的交点为(2.5,0),
故S△ABC==3.
【点睛】
本题考查了抛物线与x轴的交点,二次函数的性质,求一次函数解析式.解题的关键是明确题意,利用二次函数的性质解答.
24.(1);(2)存在,或
【分析】
(1)由直线y=x﹣4与坐标轴分别交于点B、点C,求出点B、点C的坐标,由y=x﹣4与y=﹣x2+2x组成方程组,求得方程组的解即可求得点A的坐标,再由点A,B的坐标根据勾股定理,求出线段AB的长;
(2)由OB=OC=4,∠BOC=90°,可得∠BCD=∠ABO=135°,若△BCD与△OAB相似,则∠BCD与∠ABO一定是对应角,点D一定在OC的延长线上,再根据相似三角形的对应边成比例列出方程,即可求出线段CD的长,从而求得点D的坐标.
【详解】
解:(1)∵直线y=x﹣4与坐标轴分别交于点B、点C,
∴B(0,-4),C(4,0),
由,得,,
∴A(-2,-6),
∴AB=,
(2)存在,
∵OB=OC=4,∠BOC=90°,
∴BC=,∠OBC=∠OCB=45°,
∴∠BCD=∠ABO=135°,
如图1,当∠CBD=∠BOA时,△CBD∽△BOA,
∴,
∴,
解得CD=4,
∴OD=4+4=8,
∴D(8,0),
如图2,当∠CBD=∠BAO时,△CBD∽△BAO,
∴,
∴,
解得DC=8,
∴OD=4+8=12,
∴D(12,0),
综上所述,点D的坐标为或.
【点睛】
本题考查了二次函数图象与性质,两点之间的距离公式,解二元一次方程组,及相似三角形的判定与性质.解(2)题的关键是抓住题中OB=OC这一隐含条件,可得出∠BCD=∠ABO=135°,则∠BCD和∠ABO这两个角相等,再按照∠CBD=∠BOA或∠CBD=∠BAO分类讨论,求出点D坐标.
25.(1)10;(2)见解析;(3)的最小值为,直线l的解析式为
【分析】
(1)证明△ADM≌△ECM即可;
(2)过点M任意作直线CD,交OA于点C,交OB于点D,证明<即可;
(3)过点P作PB⊥x轴,垂足为B,过点M作MC⊥x轴,垂足为C,利用平行线分线段成比例定理,三角形的中位线定理,求得CQ,PB的长,确定直线上的点的坐标求解即可.
【详解】
(1)∵ADBC,点M是CD的中点,
∴∠ADM=∠ECM,∠DAM=∠CEM,DM=CM,
∴△ADM≌△ECM,
∴= =,
∵=10,
∴=10,
故答案为:10;
(2)过点M任意作直线CD,交OA于点C,交OB于点D,设MC>MD,过点P作PE∥OB,交CM于点E,根据(1)的结论,当M为PQ的中点时,得=,
∵+=
∴<,
∴当点M恰好是PQ中点时,最小,
(3)如图,根据(1)结论,得当PM=QM时,最小,
过点P作PB⊥x轴,垂足为B,过点M作MC⊥x轴,垂足为C,
∴MC∥PB,
∵PM=MQ,
∴QC=CB,PB=2MC,
∵∠MOC=30°,OM=3,
∴MC=OMsin30°=,OC=OMcos30°=,
∴OQ+QC=OC=,PB=3,
∴2OQ+2QC=,
∵∠POB=45°,PB=3,
∴OB=3,
∴OQ+2QC=OB=3,
∴OQ=-3,
∴==;
∵OQ=-3,PB=OB=3,
∴Q(-3,0),P(3,3),
设直线PQ的解析式为y=kx+b,根据题意,得,
解得,
∴直线PQ的解析式为y=()x.
【点睛】
本题考查了三角形的全等和性质,一次函数的解析式,三角函数,中位线定理,平行线分线段成比例定理,面积的最小值,通过构造高线,平行线,为中位线定理,平行线分线段成比例定理的使用创造条件是解题的关键.
2023年陕西省西安市碑林区中考数学一模试卷(含答案): 这是一份2023年陕西省西安市碑林区中考数学一模试卷(含答案),共24页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2023年陕西省西安市灞桥区中考数学一模试卷 (含答案): 这是一份2023年陕西省西安市灞桥区中考数学一模试卷 (含答案),共25页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
陕西省西安市2021年中考数学八模试题Word版: 这是一份陕西省西安市2021年中考数学八模试题Word版,共6页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












