2021年云南省昭通市镇雄县中考数学一模试题（word版 含答案）

这是一份2021年云南省昭通市镇雄县中考数学一模试题（word版 含答案），共23页。试卷主要包含了填空题，单选题，解答题等内容，欢迎下载使用。

2021年云南省昭通市镇雄县中考数学一模试题
学校:___________姓名：___________班级：___________考号：___________


一、填空题
1．如果一个数与﹣2021互为相反数，那么这个数是__．
2．2020年6月23日，我国的北斗卫星导航系统（BDS）星座部署完成，其中一颗中高轨道卫星高度大约是21500000米．将数字21500000用科学记数法表示为______．
3．分解因式：x3﹣4xy2=_____．
4．如图，梯子的各条横档互相平行，若，则_____．

5．某校为了丰富学生的校园生活，准备购买一批陶笛．已知A型陶笛比B型陶笛的单价低20元，用2700元购买A型陶笛与用4500元购买B型陶笛的数量相同，设A型陶笛的单价为元，根据题意列出正确的方程是_______________________．
6．如图，ABC是边长为1的等边三角形，取BC边中点E，作ED∥AB，EF∥AC，得到四边形EDAF，它的周长记作C1；取BE中点E1，作E1D1∥FB，E1F1∥EF，得到四边形E1D1FF1，它的周长记作C2．照此规律作下去，则C2021＝___．


二、单选题
7．下列各数中，是无理数的是（ ）
A．-1 B．0 C． D．
8．当为何值时，在实数范围内有意义（ ）
A． B． C． D．
9．以下甲骨文汉字中，是轴对称图形但不是中心对称图形的是（ ）
A． B． C． D．
10．下列计算正确的是（ ）
A． B． C． D．
11．下列说法正确的是（ ）
A．“买一张电影票，座号是5的倍数”是必然事件
B．了解全国快递包裹产生的包装垃圾数量适合采用全面调查（普查）方式
C．“明天降雨的概率为”，意味着明天一定有半天都在降雨
D．一组数据的方差越小，则这组数据的波动也越小
12．反比例函数与一次函数在同一平面直角坐标系中的图象可能是（ ）
A． B．
C． D．
13．如图，在ABC中，∠CAB＝70°，在同一平面内，将ABC绕点A旋转到的位置．使得，则旋转角为（　　）

A．30° B．40° C．50° D．80°
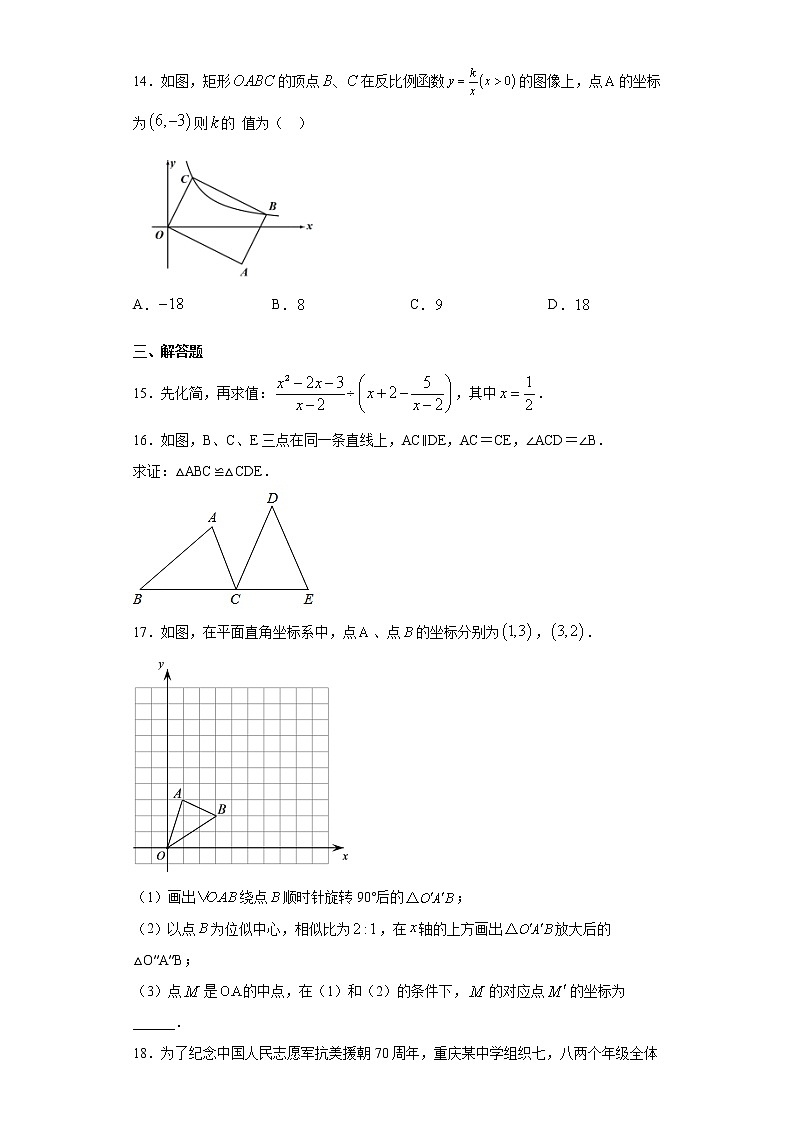
14．如图，矩形的顶点在反比例函数的图像上，点的坐标为则的 值为（ ）

A． B． C． D．

三、解答题
15．先化简，再求值：，其中．
16．如图，B、C、E三点在同一条直线上，AC∥DE，AC＝CE，∠ACD＝∠B．
求证：△ABC≌△CDE．

17．如图，在平面直角坐标系中，点、点的坐标分别为，．

（1）画出绕点顺时针旋转90°后的；
（2）以点为位似中心，相似比为，在轴的上方画出放大后的△O″A″B；
（3）点是的中点，在（1）和（2）的条件下，的对应点的坐标为______．
18．为了纪念中国人民志愿军抗美援朝70周年，重庆某中学组织七，八两个年级全体学生观看大型电视纪录片《为了和平》，并组织学生参加《中国人民志愿军抗美援朝知识知多少》测试，学校从两个年级中各随机抽取20名同学的测试成绩，并对他们的成绩（单位：分）进行统计，分析，过程如下：
收集数据：
七年级：85 80 95 100 90 95 85 65 75 85 90 90 70 90 100 80 80 90 95 75
八年级：80 60 80 95 65 100 90 85 85 80 95 75 80 90 70 80 95 75 100 90
整理数据：
成绩x（分）




七年级
2
5
8
5
八年级
3
7
5
5
分析数据：
统计量
平均数
中位数
众数
七年级
85.75
a
90
八年级
83.5
82.5
b
应用数据：
（1）请直接写出上述表中______，______；
（2）根据以上数据，你认为该校七，八年级中哪个年级学生观看完纪录片后对抗美援朝知识了解情况更好？请说明理由（写出一条理由即可）；
（3）该校七，八年级共2000名学生参与作答，估计成绩大于90分的学生人数共有多少人？
19．自从我国全面实行二孩政策后，甲、乙两个家庭都有了各自的规划，假定生男生女的概率相同，请回答下列问题：
（1）甲家庭已经有一个男孩，求第二个孩子是女孩的概率；
（2）乙家庭目前没有孩子，计划生两个孩子，请用列表法或树状图求至少有一个孩子是女孩的概率．
20．如图所示，在正方形ABCD中，对角线BD所在的直线上有两点E，F（点E，F在正方形ABCD的外部），满足BE＝DF，连接AE，AF，CE，CF．
（1）求证：四边形AECF是菱形；
（2）若AB＝4，sin∠AFE＝，求四边形AECF的面积．

21．计划对河道进行改造，现有甲乙两个工程队参加改造施工，受条件限制，每天只能由一个工程队施工．若甲工程队先单独施工天，再由乙工程队单独施工天，则可以完成米施工任务：若甲工程队先单独施工天，再由乙工程对单独施工天，则可以完成米的施工任务．
（1）求甲、乙两个工程队平均每天分别能完成多少米施工任务？
（2）该河道全长米，若两队合作工期不能超过天，乙工程队至少施工多少天？
22．如图，在△ABC中，∠C＝90°，点O在AC上，以OA为半径的⊙O交AB于点D，BD的垂直平分线交BC于点E，交BD于点F，连接DE．
（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）若AC＝3，BC＝4，OA＝1，求线段DE的长．

23．如图1，抛物线y＝﹣x2＋bx＋c与x轴相交于点A（﹣1，0）和点B，交y轴于点C，CO＝3AO，点P是抛物线上第一象限内的一动点，点Q在抛物线上．
（1）求抛物线的解析式；
（2）过点P作PD∥y轴交BC于点D，求线段PD长度的最大值；
（3）如图2，当BQ交y轴于点M，∠QBC＝∠PBC，∠BCP＝45°，求点M的坐标．



参考答案
1．2021
【分析】
直接利用相反数的定义得出答案．
【详解】
解：∵一个数与﹣2021互为相反数，
∴这个数是2021，
故答案是：2021．
【点睛】
本题考查相反数的定义，正确理解相反数是解此题的关键．
2．
【分析】
对于一个绝对值较大的数，用科学记数法写成a×10n的形式，其中1≤|a|＜10，n是比原整数位数少1的数．
【详解】
解：21500000=．
故答案为：．
【点睛】
此题考查了科学记数法的表示方法，科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．
3．x（x+2y）（x﹣2y）
【详解】
分析：原式提取x，再利用平方差公式分解即可．
详解：原式=x（x2-4y2）=x（x+2y）（x-2y），
故答案为x（x+2y）（x-2y）
点睛：此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
4．105°
【分析】
依据AB∥CD，可得∠1=∠3，根据∠1-∠2=30°，即可得到∠2=∠3-30°，再根据邻补角即可得到∠3=105°．
【详解】
解：∵AB∥CD，
∴∠1=∠3，
又∵∠1-∠2=30°，
∴∠3=∠2+30°，即∠2=∠3-30°，
又∵∠3+∠2=180°，
∴∠3+∠3-30°=180°，
∴∠3=105°，
故答案为：105°．
【点睛】
本题主要考查了平行线的性质，解题时注意：两直线平行，同位角相等．
5．
【分析】
设A型陶笛的单价为x元，则B型陶笛的单价为（x+20）元，根据用2700元购买A型陶笛与用4500元购买B型陶笛的数量相同，列方程即可．
【详解】
设A型陶笛的单价为x元，则B型陶笛的单价为（x+20）元，根据用2700元购买A型陶笛与用4500元购买B型陶笛的数量相同，可得．
故答案为：．
【点睛】
本题考查了由实际问题，抽象出分式方程，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程．
6．
【分析】
根据三角形的中位线求解C1＝4×，找规律可得∁n＝4×，据此规律可求解．
【详解】
解：∵△ABC是等边三角形，
∴AB＝BC＝AC＝1，
∵E是BC的中点，ED∥AB，
∴DE是△ABC的中位线，
∴DE＝AB＝，AD＝AC＝，
∵EF∥AC，
∴四边形EDAF是菱形，
∴C1＝4×，…，
∴＝4×，
∴C2021＝4×＝，
故答案为：．
【点睛】
本题主要考查三角形形的中位线、菱形的判定及性质、平行线的性质、找规律，找出计算周长的规律是解题的关键．
7．D
【分析】
无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．
【详解】
解：A．-1是整数，属于有理数；
B．0是整数，属于有理数；
C．是分数，属于有理数；
D．是无理数；
故选D．
【点睛】
此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．
8．A
【分析】
根据分式的分母不等于0的条件及二次根式非负性解答．
【详解】
由题意得：x-1>0，
解得x>1，
故选：A．
【点睛】
此题考查未知数的取值范围的确定，掌握分式的分母不等于0的条件及二次根式非负性是解题的关键．
9．D
【分析】
根据轴对称图形和中心对称图形的定义，逐一判断选项，即可得到答案．
【详解】
A.既是中心对称图形又是轴对称图形，故本选项不符合题意，
B.是中心对称图形，但不是轴对称图形，故本选项不符合题意，
C.既不是中心对称图形也不是轴对称图形，故本选项不符合题意，
D.是轴对称图形但不是中心对称图形，故本选符合题意．
故选D．
【点睛】
本题主要考查轴对称图形和中心对称图形的定义，熟练掌握轴对称图形和中心对称图形的定义，是解题的关键．
10．A
【分析】
A.根据同类项的定义解题；
B.根据积的乘方解题；
C.根据多项式与多项式的乘法法则或完全平方公式解题；
D.根据同类项的定义解题．
【详解】
A. ，故A正确；
B. ，故B错误；
C. ，故C错误；
D. 与不是同类项，不能合并，故D错误，
故选：A．
【点睛】
本题考查整式的混合运算，涉及合并同类项、积的乘方、多项式乘以多项式等知识，是重要考点，难度较易，掌握相关知识是解题关键．
11．D
【分析】
根据随机事件的定义、抽样调查和全面调查、概率的计算以及方差的意义对每一项进行分析即可得出结果．
【详解】
解：、“买一张电影票，座号是5的倍数”是随机事件，故本选项不正确；
、了解全国快递包裹产生的包装垃圾数量适合采用抽样调查，故本选项不正确；
、“明天降雨的概率为”，意味着明天有可能下雨，故本选项不正确；
、一组数据的方差越小，则这组数据的波动也越小，故本选项正确；
故选：．
【点睛】
本题主要考查了方差、随机事件的定义，以及概率的计算，可能性等于所求情况数与总情况数之比，比较简单．
12．C
【分析】
先根据一次函数的性质判断出m取值，再根据反比例函数的性质判断出m的取值，二者一致的即为正确答案．
【详解】
解：A、由函数y＝mx﹣m的图象可知m>0，由函数的图象可知m<0，相矛盾，故错误；
B、由函数y＝mx﹣m的图象可知m＜0，﹣m＞0，由函数的图象可知m＞0，错误；
C、由函数y＝mx﹣m的图象可知m＞0，﹣m＜0，由函数的图象可知m＞0，正确；
D、由函数y＝mx﹣m的图象可知m＜0，﹣m＜0，由函数的图象可知m＜0，相矛盾，故错误；
故选：C．
【点睛】
本题主要考查了反比例函数的图象性质和一次函数的图象性质，要掌握它们的性质才能灵活解题．
13．B
【分析】
由平行线的性质得出∠C′CA＝∠CAB＝70°，由等腰三角形的性质得出∠ACC′＝∠AC′C，运用三角形的内角和定理求出∠CAC′＝40°即可解决问题．
【详解】
解：∵CC′∥AB，∠CAB＝70°，
∴∠C′CA＝∠CAB＝70°，
又∵C、C′为对应点，点A为旋转中心，
∴AC＝AC′，即△ACC′为等腰三角形，
∴∠ACC′＝∠AC′C，
∴∠BAB′＝∠CAC′＝180°﹣2∠C′CA＝40°．
即旋转角为40°．
故选：B．
【点睛】
本题考查了旋转的基本性质，对应点到旋转中心的距离相等，对应点与旋转中心的连线的夹角为旋转角．同时考查了平行线的性质及等腰三角形的性质．
14．B
【分析】
过点C作CD⊥x轴于点D，过点B作BE⊥CD轴于点E，过点A作AF⊥x轴于点F．通过证得△COD≌△OAF得出OD=AF=3，CD=OF=6，再证明，得到CD=2OD，故设C（a，2a），则B（a+6，2a-3），得，求出a值，可求出点C坐标，即可求得k的值．
【详解】
解：过点C作CD⊥x轴于点D，过点B作BE⊥CD轴于点E，过点A作AF⊥x轴于点F．

∵四边形OABC是矩形，
∴∠COD+∠AOD=90°=∠OAF+∠AOF，OA=CB，
∴∠COD=∠OAF，
∵∠COD+∠OCD=90°，∠OCD+∠BCE=90°，
∴∠COD=∠BCE，
∴∠BCE=∠OAF，
在△BCE和△OAF中，
,
∴△BCE≌△OAF（AAS），
∴CE=AF，BE=OF，
∵点A坐标为（6，-3），
∴AF=3，OF=6，
∴CE=3，BE=6，
∵∠COD=∠OAF，∠ODC=∠OFA=90°
∴
∴
∴
∴
设C（a，2a），则B（a+6，2a-3），
∵顶点C、B在反比例函数的图象上，
∴
∴，
∴C（2，4），
∴k=2×4=8，
故选：B．
【点睛】
本题考查了反比例函数图象上点的坐标特征，矩形的性质，相似三角形的判定与性质，全等三角形的判定与性质，求得C的坐标是解题的关键．
15．，．
【分析】
先将括号内的式子通分并计算，把通分后的分子部分运用平方差公式进行因式分解，括号外分式的分子部分用十字相乘法分解因式，然后进行化简求值即可．
【详解】
解：



当时，原式．
【点睛】
本题主要考查了分式的除法运算，运用因式分解法进行分式化简是解题关键．
16．见解析．
【分析】
首先根据AC∥DE，利用平行线的性质可得：∠ACB=∠E，∠ACD=∠D，再根据∠ACD=∠B证出∠D=∠B，再由∠ACB=∠E，AC=CE可根据三角形全等的判定定理AAS证出△ABC≌△CDE．
【详解】
证明：∵AC∥DE，
∴，．
又∵，
∴，
又∵，
∴．
【点睛】
此题主要考查了全等三角形的判定，关键是熟练掌握判定两个三角形全等的方法：SSS、SAS、ASA、AAS，选用哪一种方法，取决于题目中的已知条件．
17．（1）见解析；（2）见解析；（3）（2，7）．
【分析】
（1）根据旋转的性质即可画出△OAB绕点B顺时针旋转90°后的△O′A′B；
（2）根据位似变换即可以点B为位似中心，相似比为2：1，在x轴的上方画出△O′A′B放大后的△O″A″B；
（3）根据（2）中的图形，即可得M的对应点M′的坐标．
【详解】
解：（1）如图，△O′A′B即为所求；

（2）如图，△O″A″B即为所求；

（3）如图，∵点M是OA的中点，
∴M的对应点M′的坐标为（2，7）．
故答案为：（2，7）．
【点睛】
本题考查了作图-位似变换、作图-旋转变换，解决本题的关键是掌握位似变换和旋转变换的性质．
18．（1）87.5；80；（2）七年级更好，平均分更高；（3）500人
【分析】
（1）可分别按从低到高的顺序分别列出七、八年级的成绩，从而求解出中位数和众数；
（2）根据平均值，中位数，众数的意义任选其一进行分析即可得出结论；
（3）先求出调查的40人中成绩大于90分的学生人数的占比，再乘以总人数即可．
【详解】
（1）将所有数据从低到高排列：
七年级：65 70 75 75 80 80 80 85 85 85 90 90 90 90 90 95 95 95 100 100
八年级：60 65 70 75 75 80 80 80 80 80 85 85 90 90 90 95 95 95 100 100
∴七年的中位数，八年级的众数，
故答案为：87.5；80；
（2）七年级的学生了解更好，因为七年级的平均分高于八年级的平均分；
（3）（人），
∴成绩大于90分的学生人数共有500人．
【点睛】
本题考查求一组数据的中位数，众数和它们的意义，以及根据比例求解总体中符合条件的人数，熟记中位数，众数的求解方式是解题关键．
19．（1）；（2）．
【分析】
（1）直接利用概率公式求解；
（2）画树状图展示所有4种等可能的结果数，再找出至少有一个孩子是女孩的结果数，然后根据概率公式求解．
【详解】
解：（1）∵第二个孩子是可能是男孩，也可能是女孩，可能性相同，
∴第二个孩子是女孩的概率= ；
（2）画树状图为：

共有4种等可能的结果数，其中至少有一个孩子是女孩的结果数为3，
所以至少有一个孩子是女孩的概率=．
【点睛】
本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后利用概率公式计算事件A或事件B的概率．
20．（1）见解析；（2）32
【分析】
（1）连接AC，根据正方形的性质即可证明四边形AECF是菱形；
（2）根据正方形ABCD的性质和AB＝4，sin∠AFE＝，可得AC＝，EF＝，进而可得菱形AECF的面积．
【详解】
证明：（1）如图，连接AC，

∵四边形ABCD是正方形，
∴OA＝OC，OB＝OD，AC⊥EF，
∵BE＝DF，
∴OB+BE＝OD+DF，
即OE＝OF，
∵OA＝OC，OE＝OF，
∴四边形AECF是平行四边形，
∵AC⊥EF，
∴四边形AECF是菱形；
（2）∵四边形ABCD是正方形，AB＝4，AC⊥EF，
∴OA＝AB＝，
∴AC＝，
∵sin∠AFE＝＝，
∴，
∴AF＝2，
∴OF＝，
∴EF＝，
∴菱形AECF的面积＝AC•EF＝××＝32．
故答案为：32．
【点睛】
本题考查了菱形的判定与性质、正方形的性质、解直角三角形，解决本题的关键是综合运用以上知识．
21．（1）甲工程队每天能完成施工任务米，乙工程队每天能完成施工任务米；（2）乙工程队至少施工天
【分析】
（1）设甲工程队每天施工x米，乙工程队每天施工y米，根据等量关系列出二元一次方程组，即可求解；
（2）设乙工程队施工a天，根据不等量关系，列出一元一次不等式，即可求解．
【详解】
（1）设甲工程队每天施工x米，乙工程队每天施工y米，
根据题意得：，解得：，
答：甲工程队每天能完成施工任务米，乙工程队每天能完成施工任务米；
（2）设乙工程队施工a天，
根据题意得：80a+50（90-a）≥6000，
解得：a≥50，
答：乙工程队至少施工天
【点睛】
本题主要考查二元一次方程组与一元一次不等式的实际应用，找出等量关系和不等量关系，列出方程组和不等式，是解题的关键．
22．（1）直线DE是⊙O的切线，见解析；（2）
【分析】
（1）连接OD，根据线段垂直平分线的性质得ED＝EB，则∠EDB＝∠B，结合∠A＝∠ODA，利用等量代换计算出∠ODE＝90°，则OD⊥DE，然后根据切线的判定定理得到结论；
（2）作OH⊥AD于H，则AH＝DH，利用∠A的正弦可计算出OH＝，则AH＝，AD＝2AH＝，进而得BF＝，然后利用∠B的余弦计算出EB，从而得到ED的长．
【详解】
连接OD，
∵EF垂直平分BD，
∴ED＝EB，
∴∠EDB＝∠B，
∵OA＝OD，
∴∠A＝∠ODA，
∵∠A+∠B＝90°，
∴∠ODA+∠EDB＝90°，
∴∠ODE＝90°，
∴OD⊥DE，
∴直线DE是⊙O的切线；
（2）∵∠C＝90°，AC＝3，BC＝4，
∴AB=5，
作OH⊥AD于H，
∵OA＝OD，
∴AH＝DH，
∵在Rt△OAB中，sinA＝＝，
∴在Rt△OAH中，sinA＝，
∴OH＝，
∴AH＝＝，
∴AD＝2AH＝，
∴BD＝5﹣＝，
∴BF＝BD＝，
∵在Rt△ABC中，cosB＝，
在Rt△BEF中，cosB＝＝，
∴BE＝×＝，
∴DE= BE= ．

【点睛】
本题主要考查直角三角形的性质，切线的判定定理，中垂线的性质定理以及解直角三角形，添加合适的辅助线，构造直角三角形，熟练掌握锐角三角函数的定义，是解题的关键．
23．（1）y=﹣x2+2x+3；（2）；（3）M（0，1）．
【分析】
（1）用待定系数法即可求解；
（2）设点P（x，﹣x2+2x+3），则点D（x，﹣x＋3）（0＜x＜3），则，即可求解；
（3）证明△CMB≌△CPB（ASA），则CM＝CP＝2，OM＝3﹣2＝1，即可求解．
【详解】
解：（1）∵A（﹣1，0），则OA＝1，
又∵CO＝3AO，
∴OC＝3，C（0，3），
把A，C两点的坐标代入y＝﹣x2＋bx＋c得，
解得，
∴抛物线的解析式为y＝﹣x2+2x+3；
（2）由﹣x2+2x+3＝0得点B（3，0），设直线BC的解析式为y＝kx＋b，
将点B（3，0），C（0，3）代入得，解得，
∴直线BC的解析式为y＝﹣x＋3，
设点P（x，﹣x2+2x+3），则点D（x，﹣x＋3）（0＜x＜3），
∴，
∴当时，PD有最大值；
（3）∵B（3，0），C（0，3），
∴OC＝OB，
∴△BOC是等腰直角三角形，
∴∠BCO＝45°，
∵∠BCP＝45°，
∴∠BCP＝∠BCO＝45°，
∴CP∥OB，
设P（t，3），代入抛物线y＝﹣x2＋2x＋3得P（2，3），
故CP＝2﹣0＝2，
在△CMB和△CPB中，
，
∴△CMB≌△CPB（ASA），
∴CM＝CP＝2，
∴OM＝3﹣2＝1，
∴点M（0，1）．
【点评】
本题是二次函数综合题，主要考查了一次函数的性质、三角形全等、等腰直角三角形的性质等，有一定的综合性，难度适中．