2021年湖北省荆门市中考模拟卷-数学（附答案）

这是一份2021年湖北省荆门市中考模拟卷-数学（附答案），共5页。试卷主要包含了下列实数中的无理数是，下列式子中，计算正确的是，估计等内容，欢迎下载使用。

荆门市2021年初中毕业生学业考试命题大赛（数学）试卷
一．选择题（共12小题）
1．下面四个几何体中，其中主视图不是中心对称图形的是（　　）




2．下列实数中的无理数是（　　）
A． B． C． D．
3．下列式子中，计算正确的是（　　）
A．（﹣a﹣b）2＝a2﹣2ab+b2 B．（a+2）（a﹣2）＝a2﹣2
C．（a+5）（a﹣2）＝a2+3a﹣10 D．3a3•2a2＝6a6
4．估计（2﹣）•的值应在（　　）
A．1和2之间 B．2和3之间 C．3和4之间 D．4和5之间
5．已知x+y＝4，x﹣y＝，则式子（x﹣y+）（x+y﹣）的值是（　　）
A．48 B．12 C．16 D．12
6．如图，在平面直角坐标系中，直线l1：y＝﹣x+1与x轴，y轴分别交于点A和点B，直线l2：y＝kx（k≠0）与直线l1在第一象限交于点C．若∠BOC＝∠BCO，则k的值为（　　）
A． B． C． D．2
7．如图，平行四边形ABCD的周长是26cm，对角线AC与BD交于点O，AC⊥AB，E是BC中点，△AOD的周长比△AOB的周长多3cm，则AE的长度为（　　）
A．3cm B．4cm C．5cm D．8cm
8．若数a使关于x的不等式组，有且仅有三个整数解，且使关于y的分式方程+＝1有整数解，则满足条件的所有a的值之和是（　　）
A．﹣10 B．﹣12 C．﹣16 D．﹣18
6题图
7题图







9． 如图1，在矩形ABCD中，点E在CD上，∠AEB＝90°，点P从点A出发，沿A→E→B的路径匀速动
到点B停止，作PQ⊥CD于点Q，设点P运动的路程为x，PQ长为y，若y与x之间的函数关系图象如图2所示，当x＝6时，PQ的值是（　　）
A．2 B． C． D．1
10．如图，已知点E是矩形ABCD的对角线AC上的一动点，正方形EFGH的顶点G、H都在边AD上，若AB＝3，BC＝4，则tan∠AFE的值（　　）
A．等于 B．等于 C．等于 D．随点E位置的变化而变化
11．如图，一次函数y＝2x与反比例函数y＝（k＞0）的图象交于A，B两点，点P在以C（﹣2，0）为圆心，1为半径的⊙C上，Q是AP的中点，已知OQ长的最大值为，则k的值为（　　）
A． B． C． D．
12．如图，抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝﹣2，与x轴的一个交点在（﹣3，0）和
（﹣4，0）之间，其部分图象如图所示．则下列结论：①4a﹣b＝0；②c＜0；③﹣3a+c＞0；
④4a﹣2b＞at2+bt（t为实数）；⑤点（﹣，y1），（﹣，y2），（﹣，y3）是该抛物线上的点，
则y1＜y2＜y3，正确的个数有（　　）
A．4个 B．3个 C．2个 D．1个
12题图
11题图
10题图







二．填空题（共5小题）
13．已知一组数据﹣1，0，4，x，8，10．这组数据的众数为8，则这组数据的中位数是　 　．
14．分解因式：（x+9）（x﹣1）﹣8x= ．
15．关于x的一元二次方程x2﹣2kx+k2﹣k＝0的两个实数根分别是x1、x2，且x12+x22＝4，则x12﹣x1x2+x22的值是　 　．
16．飞机着陆后滑行的距离y（单位：m）关于滑行时间t（单位：s）的函数解析式是y＝60t﹣．在飞机着陆滑行中，最后4s滑行的距离是　 　m．
17．已知a＞0，S1＝，S2＝﹣S1﹣1，S3＝，S4＝﹣S3﹣1，S5＝，…（即当n为大于1的奇数时，Sn＝；当n为大于1的偶数时，Sn＝﹣Sn﹣1﹣1），按此规律，S2019＝　 　．
三．解答题（共8小题）
18．（1）计算：
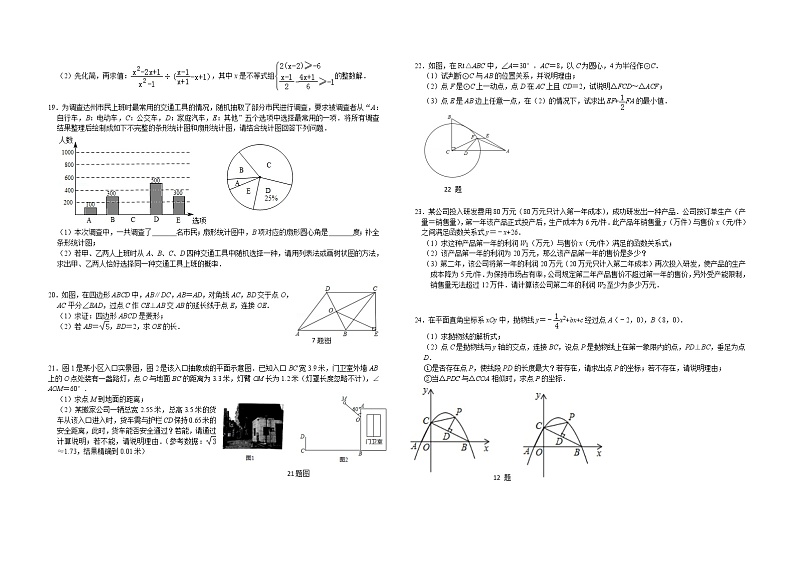
（2）先化简，再求值：，其中x是不等式组的整数解．

22题图
19．为调查达州市民上班时最常用的交通工具的情况，随机抽取了部分市民进行调查，要求被调查者从“A：自行车，B：电动车，C：公交车，D：家庭汽车，E：其他”五个选项中选择最常用的一项．将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图，请结合统计图回答下列问题．

（1）本次调查中，一共调查了　 　名市民；扇形统计图中，B项对应的扇形圆心角是　 　度；补全条形统计图；
（2）若甲、乙两人上班时从A、B、C、D四种交通工具中随机选择一种，请用列表法或画树状图的方法，求出甲、乙两人恰好选择同一种交通工具上班的概率．

7题图

20．如图，在四边形ABCD中，AB∥DC，AB＝AD，对角线AC，BD交于点O，AC平分∠BAD，过点C作CE⊥AB交AB的延长线于点E，连接OE．
（1）求证：四边形ABCD是菱形；
（2）若AB＝，BD＝2，求OE的长．



21．图1是某小区入口实景图，图2是该入口抽象成的平面示意图．已知入口BC宽3.9米，门卫室外墙AB上的O点处装有一盏路灯，点O与地面BC的距离为3.3米，灯臂OM长为1.2米（灯罩长度忽略不计），∠AOM＝60°．
21题图
（1）求点M到地面的距离；
（2）某搬家公司一辆总宽2.55米，总高3.5米的货车从该入口进入时，货车需与护栏CD保持0.65米的安全距离，此时，货车能否安全通过？若能，请通过计算说明；若不能，请说明理由．（参考数据：≈1.73，结果精确到0.01米）




22．如图，在Rt△ABC中，∠A＝30°，AC＝8，以C为圆心，4为半径作⊙C．
（1）试判断⊙C与AB的位置关系，并说明理由；
（2）点F是⊙C上一动点，点D在AC上且CD＝2，试说明△FCD～△ACF；
（3）点E是AB边上任意一点，在（2）的情况下，试求出EF+FA的最小值．









23．某公司投入研发费用80万元（80万元只计入第一年成本），成功研发出一种产品．公司按订单生产（产量＝销售量），第一年该产品正式投产后，生产成本为6元/件．此产品年销售量y（万件）与售价x（元/件）之间满足函数关系式y＝﹣x+26．
（1）求这种产品第一年的利润W1（万元）与售价x（元/件）满足的函数关系式；
（2）该产品第一年的利润为20万元，那么该产品第一年的售价是多少？
（3）第二年，该公司将第一年的利润20万元（20万元只计入第二年成本）再次投入研发，使产品的生产成本降为5元/件．为保持市场占有率，公司规定第二年产品售价不超过第一年的售价，另外受产能限制，销售量无法超过12万件．请计算该公司第二年的利润W2至少为多少万元．


24．在平面直角坐标系xOy中，抛物线y＝﹣x2+bx+c经过点A（﹣2，0），B（8，0）．
（1）求抛物线的解析式；
（2）点C是抛物线与y轴的交点，连接BC，设点P是抛物线上在第一象限内的点，PD⊥BC，垂足为点D．
①是否存在点P，使线段PD的长度最大？若存在，请求出点P的坐标；若不存在，请说明理由；
②当△PDC与△COA相似时，求点P的坐标．
12题图











参考答案与试题解析
一．选择题（共12小题）
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
C
C
B
D
B
B
B
C
A
C
B
二．填空题（共6小题）
13． 6 ；14． （x+3）（x﹣3） ；15． 　4 ；16． 24 ；17．﹣ 。
三．解答题（共8小题）
18．解：（1）原式＝2﹣3﹣1﹣2＝﹣6；
（2）解：，
解不等式①得，x≥﹣1，
解不等式②得，x≤2，
所以，不等式组的解集是﹣1≤x≤2，
∵x是整数，
∴x＝0，±1，2，
÷（﹣x+1），
＝÷，
＝•，
＝﹣，
要使分式有意义，则（x+1）（x﹣1）≠0，x≠0，
解得x≠±1，x≠0，
所以，x＝2，
原式＝﹣．
19． （1）本次调查中，一共调查了　2000　名市民；扇形统计图中，B项对应的扇形圆心角是　54　度；补全条形统计图；
（2）若甲、乙两人上班时从A、B、C、D四种交通工具中随机选择一种，请用列表法或画树状图的方法，求出甲、乙两人恰好选择同一种交通工具上班的概率．
解：（1）本次调查的总人数为500÷25%＝2000人，扇形统计图中，B项对应的扇形圆心角是360°×＝54°，
C选项的人数为2000﹣（100+300+500+300）＝800，
补全条形图如下：

故答案为：2000、54；
（2）列表如下：

A
B
C
D
A
（A，A）
（B，A）
（C，A）
（D，A）
B
（A，B）
（B，B）
（C，B）
（D，B）
C
（A，C）
（B，C）
（C，C）
（D，C）
D
（A，D）
（B，D）
（C，D）
（D，D）
由表可知共有16种等可能结果，其中甲、乙两人恰好选择同一种交通工具上班的结果有4种，
所以甲、乙两人恰好选择同一种交通工具上班的概率为＝．
20．如图，在四边形ABCD中，AB∥DC，AB＝AD，对角线AC，BD交于点O，AC平分∠BAD，过点C作CE⊥AB交AB的延长线于点E，连接OE．
（1）求证：四边形ABCD是菱形；（2）若AB＝，BD＝2，求OE的长．

解：（1）∵AB∥CD，∴∠OAB＝∠DCA，∵AC为∠DAB的平分线，
∴∠OAB＝∠DAC，∴∠DCA＝∠DAC，∴CD＝AD＝AB，
∵AB∥CD，∴四边形ABCD是平行四边形，∵AD＝AB，∴▱ABCD是菱形；
（2）∵四边形ABCD是菱形，
∴OA＝OC，BD⊥AC，∵CE⊥AB，∴OE＝OA＝OC，
∵BD＝2，∴OB＝BD＝1，在Rt△AOB中，AB＝，OB＝1，∴OA＝＝2，∴OE＝OA＝2．
21.解：（1）如图，过M作MN⊥AB于N，交BA的延长线于N，
Rt△OMN中，∠NOM＝60°，OM＝1.2，
∴∠M＝30°，∴ON＝OM＝0.6，∴NB＝ON+OB＝3.3+0.6＝3.9；
即点M到地面的距离是3.9米；
（2）取CE＝0.65，EH＝2.55，
∴HB＝3.9﹣2.55﹣0.65＝0.7，
过H作GH⊥BC，交OM于G，过O作OP⊥GH于P，
∵∠GOP＝30°，
∴tan30°＝＝，
∴GP＝OP＝≈0.404，
∴GH＝3.3+0.404＝3.704≈3.70＞3.5，
∴货车能安全通过．
22．如图，在Rt△ABC中，∠A＝30°，AC＝8，以C为圆心，4为半径作⊙C．
（1）试判断⊙C与AB的位置关系，并说明理由；
（2）点F是⊙C上一动点，点D在AC上且CD＝2，试说明△FCD～△ACF；
（3）点E是AB边上任意一点，在（2）的情况下，试求出EF+FA的最小值．

【解答】（1）解：结论：相切．
理由：作CM⊥AB于M．
在Rt△ACM中，∵∠AMC＝90°，∠CAM＝30°，AC＝8，
∴CM＝AC＝4，
∵⊙O的半径为4，
∴CM＝r，∴AB是⊙C的切线．
（2）证明：
∵CF＝4，CD＝2，CA＝8，
∴CF2＝CD•CA，
∴＝，∵∠FCD＝∠ACF，
∴△FCD∽△ACF．
（3）解：作DE′⊥AB于E′，交⊙C于F′．
∵△FCD∽△ACF，
∴＝＝，
∴DF＝AC，∴EF+AF＝EF+DF，∴欲求EF+AF的最小值，就是要求EF+DF的最小值，
当E与E′，F与F′重合时，EF+DF的值最小，最小值＝DE′＝AD＝3．
【点评】本题考查圆综合题、切线的判定和性质、相似三角形的判定和性质，垂线段最短等知识，解题的关键是学会添加常用辅助线，正确切线的证明方法，学会正确寻找相似三角形解决问题，学会利用垂线段最短解决问题，属于中考压轴题．
23． 解：（1）W1＝（x﹣6）（﹣x+26）﹣80＝﹣x2+32x﹣236．
（2）由题意：20＝﹣x2+32x﹣236．
解得：x＝16，
答：该产品第一年的售价是16元．
（3）∵公司规定第二年产品售价不超过第一年的售价，另外受产能限制，销售量无法超过12万件．
∴14≤x≤16，
W2＝（x﹣5）（﹣x+26）﹣20＝﹣x2+31x﹣150，
∵抛物线的对称轴x＝15.5，又14≤x≤16，
∴x＝14时，W2有最小值，最小值＝88（万元），
答：该公司第二年的利润W2至少为88万元．
【点评】本题考查二次函数的应用、一元二次方程的应用等知识，解题的关键是理解题意，学会构建方程或函数解决问题，属于中考常考题型．
24．【解答】解：（1）把A（﹣2，0），B（8，0）代入抛物线y＝﹣x2+bx+c，
得：，解得：，
∴抛物线的解析式为：y＝﹣x2+x+4；
（2）由（1）知C（0，4），∵B（8，0），
易得直线BC的解析式为：y＝﹣x+4，
①如图1，过P作PG⊥x轴于G，PG交BC于E，
Rt△BOC中，OC＝4，OB＝8，
∴BC＝＝4，
在Rt△PDE中，PD＝PE•sin∠PED＝PE•sin∠OCB＝PE，
∴当线段PE最长时，PD的长最大，
设P（t，﹣），则E（t，），
∴PG＝﹣，EG＝﹣t+4，
∴PE＝PG﹣EG＝（﹣）﹣（﹣t+4）＝﹣t2+2t＝﹣（t﹣4）2+4，（0＜t＜8），
当t＝4时，PE有最大值是4，此时P（4，6），
∴PD＝＝，
即当P（4，6）时，PD的长度最大，最大值是；
②∵A（﹣2，0），B（8，0），C（0，4），
∴OA＝2，OB＝8，OC＝4，
∴AC2＝22+42＝20，AB2＝（2+8）2＝100，BC2＝42+82＝80，
∴AC2+BC2＝AB2，
∴∠ACB＝90°，
∴△COA∽△BOC，
当△PDC与△COA相似时，就有△PDC与△BOC相似，
∵相似三角形的对应角相等，
∴∠PCD＝∠CBO或∠PCD＝∠BCO，
（I）若∠PCD＝∠CBO时，即Rt△PDC∽Rt△COB，
此时CP∥OB，
∵C（0，4），
∴yP＝4，
∴﹣＝4，
解得：x1＝6，x2＝0（舍），
即Rt△PDC∽Rt△COB时，P（6，4）；
（II）若∠PCD＝∠BCO时，即Rt△PDC∽Rt△BOC，
如图2，过P作x轴的垂线PG，交直线BC于F，
∴PF∥OC，
∴∠PFC＝∠BCO，
∴∠PCD＝∠PFC，
∴PC＝PF，
设P（n，﹣+n+4），则PF＝﹣+2n，
过P作PN⊥y轴于N，
Rt△PNC中，PC2＝PN2+CN2＝PF2，
∴n2+（﹣+n+4﹣4）2＝（﹣+2n）2，
解得：n＝3，
即Rt△PDC∽Rt△BOC时，P（3，）；
综上所述，当△PDC与△COA相似时，点P的坐标为（6，4）或（3，）．


【点评】本题考查二次函数综合题、一次函数的应用、勾股定理的逆定理、锐角三角函数、相似三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，学会根据方程解决问题，属于中考压轴题．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布