






还剩49页未读,
继续阅读
所属成套资源:人教B版数学必修第四册全册同步优质课件
成套系列资料,整套一键下载
高中人教B版 (2019)第十一章 立体几何初步11.1 空间几何体11.1.2 构成空间几何体的基本元素多媒体教学课件ppt
展开
这是一份高中人教B版 (2019)第十一章 立体几何初步11.1 空间几何体11.1.2 构成空间几何体的基本元素多媒体教学课件ppt,共57页。PPT课件主要包含了激趣诱思,知识点拨,答案B,解析如图,探究一,探究二,探究三,探究四,探究五,素养形成等内容,欢迎下载使用。
国家体育场的主体建筑“鸟巢”主要由巨大的门式钢架组成,共有24根桁架柱,其结构科学简单,设计新颖独特,为国际上极富特色的巨型建筑.与“鸟巢”相呼映的是“水立方”——国家游泳中心.国家游泳中心也是北京奥运会标志性建筑,它以冰晶状的亮丽身姿,装点着奥林匹克公园.你能说出它们作为一个空间几何体是由哪些基本元素构成的吗?
知识点一:空间中的点、线、面1.几何里所说的“平面”,是从课桌面、黑板面、平静的湖面这样的一些物体中抽象出来的.几何里的平面是无限延展的.2.长方体、圆柱、圆锥、球等都是几何体(几何体也简称为“体”),包围着几何体的是“面”,面与面相交给人“线”的形象,线与线相交给人“点”的形象.这就是说,可以将点、线、面看作构成空间几何体的基本元素.另外,点运动的轨迹可以是线,线运动的轨迹可以是面,面运动的轨迹可以是体.
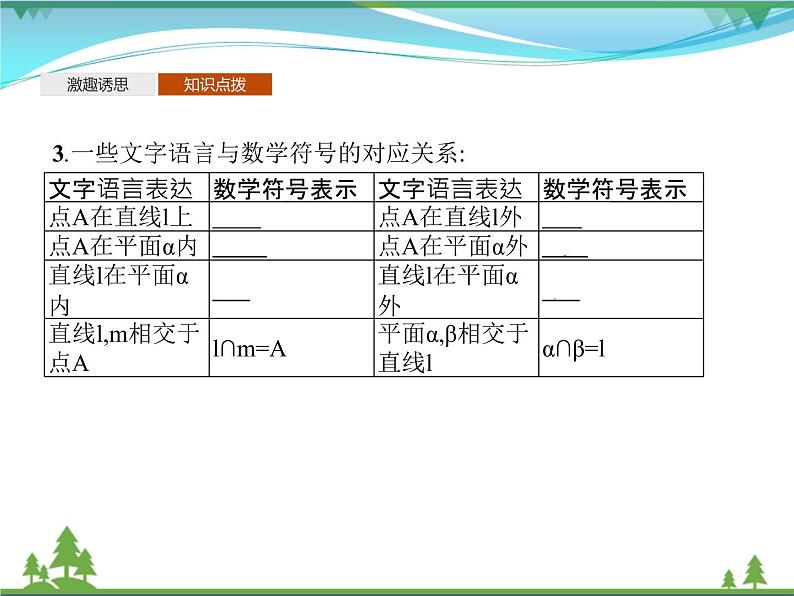
3.一些文字语言与数学符号的对应关系:
微思考平静的湖面、课桌面、黑板面、一望无垠的草原给你什么样的感觉?问题1:生活中的平面有大小之分吗?提示:有.问题2:几何中的“平面”是怎样的?提示:从物体中抽象出来的,绝对平,无大小之分.
微练习(1)图①的平面可表示为 、 、 或 .
(2)在图①中,A∈AB,B AB,C AB, (3)在图②中,E∈EF,E∈AB,则AB∩EF= .EF⊂α,EF⊂β,则α∩β= .
答案:(1)(答案不唯一)平面α 平面ABC 平面ABD 平面ABCD (2)∈ ∉ (3)E EF
知识点二:空间中点与直线、直线与直线的位置关系1.空间中点与直线的位置关系.
2.空间中直线与直线的位置关系.
名师点析 不能误认为分别在不同平面内的两条直线为异面直线.如图所示,
虽然有a⊂α,b⊂β,即a,b分别在两个不同的平面内,但是因为a∩b=O,所以a与b不是异面直线.
微判断(1)没有公共点的两条直线是平行直线.( )(2)互相垂直的两条直线是相交直线.( )(3)既不平行又不相交的两条直线是异面直线.( )(4)不在同一平面内的两条直线是异面直线.( )答案:(1)× (2)× (3)√ (4)×
微练习1若空间两条直线a和b没有公共点,则a与b的位置关系是( ) A.共面B.平行C.异面D.平行或异面答案:D解析:若直线a和b共面,则由题意可知a∥b;若a和b不共面,则由题意可知a与b是异面直线.
微练习2一条直线与两条异面直线中的一条平行,则它和另一条的位置关系是( )A.平行或异面B.相交或异面C.异面 D.相交
在长方体ABCD-A1B1C1D1中,AA1与BC是异面直线,又AA1∥BB1,AA1∥DD1,显然BB1∩BC=B,DD1与BC是异面直线.
知识点三:空间中直线与平面、平面与平面的位置关系1.直线在平面内
不难看出,图中,点A,B确定的直线l上的所有点都在平面α内,这称为直线l在平面α内(或平面α过直线l),记作l⊂α.
2.直线在平面外直线m上至少有一个点不在平面α内,这称为直线m在平面α外,记作m⊄α;图中的m与α有且只有一个公共点(称为直线m与平面α相交),一般简写为m∩α=B.
3.直线与平面平行一般地,如果l是空间中的一条直线,α是空间中的一个平面,则l∩α≠⌀与l∩α=⌀有且只有一种情况成立.而且,当l∩α≠⌀时,要么l⊂α,要么l与α只有一个公共点;当l∩α=⌀时,称直线l与平面α平行,记作l∥α.
4.平面与平面相交如图α与β有公共点,这称为平面α与平面β相交,记作α∩β≠⌀.更进一步可以看出,一个点是α与β的公共点,当且仅当这个点在直线k上,这可记作α∩β=k.
5.平面与平面平行如果α与β是空间中的两个平面,则α∩β≠⌀与α∩β=⌀有且只有一种情况成立.而且,当α∩β≠⌀时,α与β的公共点组成一条直线;当α∩β=⌀时,称平面α与平面β平行,记作α∥β.
6.直线与平面的位置关系列表比较
7.两个平面的位置关系列表比较
名师点析 1.一般地,直线a在平面α内时,应把直线a画在表示平面α的平行四边形内,切勿画出边框外;直线a与平面α相交时,应画成直线a与平面α只有一个公共点,被平面α遮住的部分画成虚线或不画;直线a与平面α平行时,应画成直线a与表示平面α的平行四边形的一条边平行,并画在表示平面α的平行四边形外.2.画两个互相平行的平面时,要注意使表示平面的两个平行四边形的对应边平行,两个平行四边形上下放置.
微思考1“直线与平面不相交”与“直线与平面没有公共点”是相同的意义吗?提示:不是.前者包括直线与平面平行及直线在平面内这两种情况;而后者仅指直线与平面平行.微思考2分别位于两个平行平面内的两条直线有什么位置关系?提示:这两条直线没有公共点,故它们的位置关系是平行或异面.
微判断(1)若直线l上有无数个点不在平面α内,则l∥α.( )(2)如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行.( )(3)若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点.( )答案:(1)× (2)× (3)√
微练习1若M∈平面α,M∈平面β,则α与β的位置关系是( )A.平行B.相交C.异面D.不确定答案:B解析:因为M∈α,M∈β,所以α与β相交于过点M的一条直线.
微练习2空间三个平面如果每两个都相交,那么它们的交线有 条. 答案:1或3解析:空间三个平面两两相交,则有一条交线或三条交线,三条交线平行或相交于一点.
知识点四:直线与平面垂直1.直线与平面垂直的定义(1)文字语言:一般地,如果直线l与平面α相交于一点A,且对平面α内的任意一条过点A的直线m,都有l⊥m,则称直线l与平面α垂直(或l是平面α的一条垂线,α是直线l的一个垂面),记作l⊥α.其中,点A称为垂足.(2)图形语言:如图.
画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.(3)符号语言:任意m⊂α,都有l⊥m⇒l⊥α.
2.投影、点到平面的距离、直线到平面的距离、两平行平面之间的距离的定义给定空间中一个平面α及一个点A,过A可以作而且只可以作平面α的一条垂线.如果记垂足为B,则称B为A在平面α内的射影(也称为投影),线段AB为平面α的垂线段,AB的长为点A到平面α的距离.特别地,当直线与平面平行时,直线上任意一点到平面的距离称为这条直线到这个平面的距离;当平面与平面平行时,一个平面上任意一点到另一个平面的距离称为这两平行平面之间的距离.
微思考鲁班是我国古代一位出色的发明家,他在做木工时,常遇到有关直角的问题.虽然他手头有画直角的矩,但用起来很费事.于是,鲁班对矩进行改进,做成一把叫做曲尺的“L”形木尺.现在木工要检查一根木棒是否和板面垂直,只需用曲尺在不同的方向(但不是相反的方向)检查两次,如图.如果两次检查时,曲尺的两边都分别与木棒和板面密合,便可以判定木棒与板面垂直.
(1)用“L”形木尺检查一次能判定木棒与板面垂直吗?(1)提示:不能.(2)上述内容说明了直线与平面垂直的条件是什么?(2)提示:直线垂直于平面内的两条相交直线.(3)若直线垂直于平面内的无数条直线,则直线与平面垂直吗?(3)提示:不一定.
微练习直线l⊥平面α,直线m⊂α,则l与m不可能( ) A.平行B.相交C.异面D.垂直答案:A解析:∵直线l⊥平面α,∴l与α相交.∵m⊂α,∴l与m相交或异面,由直线与平面垂直的定义,可知l⊥m.故l与m不可能平行.
文字、图形、符号三种语言的转化例1用符号语言表示下列语句,并画出图形.(1)三个平面α,β,γ相交于一点P,且平面α与平面β交于PA,平面α与平面γ交于PB,平面β与平面γ交于PC;(2)平面ABD与平面BCD交于BD,平面ABC与平面ADC交于AC.
解:(1)符号语言表示:α∩β∩γ=P,α∩β=PA,α∩γ=PB,β∩γ=PC.图形表示:如图①所示.
(2)符号语言表示:平面ABD∩平面BCD=BD,平面ABC∩平面ADC=AC.图形表示:如图②所示.
反思感悟 学习几何问题,三种语言间的互相转化是一种基本技能.要注意符号语言的意义,如点与直线、点与平面间的位置关系只能用“∈”或“∉”,直线与平面间的位置关系只能用“⊂”或“⊄”.由图形语言表示点、线、面的位置关系时,要注意实线和虚线的区别.
变式训练 1(1)若点M在直线a上,a在平面α内,则M,a,α间的关系可记为 . (2)根据右图,填入相应的符号:A 平面ABC,A 平面BCD,BD 平面ABC,平面ABC∩平面ACD= . (3)根据下列条件画出图形:平面α∩平面β=MN,△ABC的三个顶点满足条件A∈MN,B∈α,B∉MN,C∈β,C∉MN.
答案:(1)M∈a,a⊂α,M∈α(2)∈ ∉ ⊄ AC(3)如图所示.
空间两条直线位置关系的判定例2已知三条直线a,b,c,a与b异面,b与c异面,则a与c有什么样的位置关系?并画图说明.
解:直线a与c的位置关系有三种情况.直线a与c可能平行,如图①;可能相交,如图②;可能异面,如图③.
反思感悟 判定两条直线位置关系的方法判定两条直线的位置关系时,若要判定直线平行或相交,可用平面几何中的定义和方法来处理;判定异面直线的方法往往根据连接平面内一点与平面外一点的直线和这个平面内不经过此点的直线是异面直线来判断.
变式训练 2 如图,在正方体ABCD-A1B1C1D1中,判断下列直线的位置关系:(1)直线A1B与直线D1C的位置关系是 ; (2)直线A1B与直线B1C的位置关系是 .
答案:(1)平行 (2)异面解析:(1)因为A1D1?B1C1,B1C1?BC,所以A1D1?BC,即四边形A1D1CB为平行四边形,所以A1B∥D1C.(2)因为直线A1B⊂平面A1B,B1∈平面A1B,且B1∉直线A1B,直线CB1⊄平面A1B,所以直线A1B与直线CB1为异面直线.
直线与平面的位置关系例3下列五个命题中正确命题的个数是( )①如果a,b是两条直线,a∥b,那么a平行于经过b的任何一个平面;②如果直线a和平面α满足a∥α,那么a与平面α内的任何一条直线平行;③如果直线a,b满足a∥α,b∥α,那么a∥b;④如果直线a,b和平面α满足a∥b,a∥α,b⊄α,那么b∥α;⑤如果a与平面α上的无数条直线平行,那么直线a必平行于平面α.A.0B.1C.2D.3
反思感悟 空间中直线与平面只有三种位置关系:直线在平面内、直线与平面相交、直线与平面平行.在判断直线与平面的位置关系时,这三种情况都要考虑到,避免遗漏.正方体(长方体)是立体几何中的重要模型,直线与平面的位置关系都可以在这个模型中得到反映,故我们可以把要判断位置关系的直线、平面放在正方体(长方体)中,以便正确作出判断,避免凭空臆断.
变式训练 3下列命题中的真命题是( )A.若点A∈α,点B∉α,则直线AB与平面α相交B.若a⊂α,b⊄α,则a与b必异面C.若点A∉α,点B∉α,则直线AB∥平面αD.若a∥α,b⊂α,则a∥b
答案:A解析:选项A正确.对于选项B,如图①显然错误.对于选项C,如图②显然错误.对于选项D,如图③显然错误.故选A.
两个平面的位置关系例4α,β是两个不重合的平面,下面说法正确的是( )A.平面α内有两条直线a,b都与平面β平行,那么α∥βB.平面α内有无数条直线平行于平面β,那么α∥βC.若直线a与平面α和平面β都平行,那么α∥βD.平面α内所有的直线都与平面β平行,那么α∥β
反思感悟 判断两平面之间的位置关系时,可把文字语言转化为图形语言,搞清图形间的相对位置是确定的还是可变的,借助于直观想象能力,确定平面间的位置关系.
变式训练 4如果在两个平面内分别有一条直线,这两条直线互相平行,那么两个平面的位置关系一定是( )A.平行B.相交 C.平行或相交D.不能确定答案:C解析:由题目分别在两个平面内的两直线平行判定两平面是相交或平行.解答本题可逆向考虑画两个平行面,看是否能在此两面内画两条平行线.同样画两相交面,看是否能在此两面内画两条平行线,再作出选择(如图所示).
直线和平面垂直的定义例5直线l与平面α内的无数条直线垂直,则直线l与平面α的关系是( )A.l和平面α平行B.l和平面α垂直C.l在平面α内 D.不能确定
答案:D解析:如图所示,直线l和平面α平行,或直线l和平面α垂直或直线l在平面α内都有可能.故选D.
反思感悟 直线和平面垂直的定义是描述性定义,对直线的任意性要注意理解.实际上,“任何一条”与“所有”表达相同的含义.当直线与平面垂直时,该直线就垂直于这个平面内的任何直线.由此可知,如果一条直线与一个平面内的一条直线不垂直,那么这条直线就一定不与这个平面垂直.
变式训练 5在长方体ABCD-A1B1C1D1中,不能作为平面ABCD垂线的是( )A.AA1B.BB1C.CC1D.AD1答案:D
线、面位置关系图形的画法典例作出下列各题的图形.(1)画直线a,b,使a∩α=A,b∥α.(2)画平面α,β,γ,使α∥β,γ∩α=m,γ∩β=n.
变式训练 在图中画出三个两两相交的平面.
1.若点Q在直线b上,b在平面β内,则Q,b,β之间的关系可记作( )A.Q∈b∈βB.Q∈b⊂βC.Q⊂b⊂βD.Q⊂b∈β答案:B解析:因为点Q(元素)在直线b(集合)上,所以Q∈b.又因为直线b(集合)在平面β(集合)内,所以b⊂β.所以Q∈b⊂β.
2.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一平面的位置关系为( )A.平行 B.相交C.直线在平面内D.平行或直线在平面内答案:D解析:由题知这条直线可能在另一平面内也可能与另一平面平行.
3.长方体的一条体对角线与长方体的棱所组成的异面直线有 对.
解析:如图所示,在长方体AC1中,与对角线AC1成异面直线的是:A1D1,BC,BB1,DD1,A1B1,DC,所以组成6对异面直线.
4.下列命题:①两个平面有无数个公共点,则这两个平面重合;②若l,m是异面直线,l∥α,m∥β,则α∥β.其中错误命题的序号为 .
答案:①②解析:对于①,两个平面相交,也有无数多个公共点,故①错误;对于②,借助于正方体ABCD-A1B1C1D1,AB∥平面DCC1D1,B1C1∥平面AA1D1D,又AB与B1C1异面,而平面DCC1D1与平面AA1D1D相交,故②错误.
国家体育场的主体建筑“鸟巢”主要由巨大的门式钢架组成,共有24根桁架柱,其结构科学简单,设计新颖独特,为国际上极富特色的巨型建筑.与“鸟巢”相呼映的是“水立方”——国家游泳中心.国家游泳中心也是北京奥运会标志性建筑,它以冰晶状的亮丽身姿,装点着奥林匹克公园.你能说出它们作为一个空间几何体是由哪些基本元素构成的吗?
知识点一:空间中的点、线、面1.几何里所说的“平面”,是从课桌面、黑板面、平静的湖面这样的一些物体中抽象出来的.几何里的平面是无限延展的.2.长方体、圆柱、圆锥、球等都是几何体(几何体也简称为“体”),包围着几何体的是“面”,面与面相交给人“线”的形象,线与线相交给人“点”的形象.这就是说,可以将点、线、面看作构成空间几何体的基本元素.另外,点运动的轨迹可以是线,线运动的轨迹可以是面,面运动的轨迹可以是体.
3.一些文字语言与数学符号的对应关系:
微思考平静的湖面、课桌面、黑板面、一望无垠的草原给你什么样的感觉?问题1:生活中的平面有大小之分吗?提示:有.问题2:几何中的“平面”是怎样的?提示:从物体中抽象出来的,绝对平,无大小之分.
微练习(1)图①的平面可表示为 、 、 或 .
(2)在图①中,A∈AB,B AB,C AB, (3)在图②中,E∈EF,E∈AB,则AB∩EF= .EF⊂α,EF⊂β,则α∩β= .
答案:(1)(答案不唯一)平面α 平面ABC 平面ABD 平面ABCD (2)∈ ∉ (3)E EF
知识点二:空间中点与直线、直线与直线的位置关系1.空间中点与直线的位置关系.
2.空间中直线与直线的位置关系.
名师点析 不能误认为分别在不同平面内的两条直线为异面直线.如图所示,
虽然有a⊂α,b⊂β,即a,b分别在两个不同的平面内,但是因为a∩b=O,所以a与b不是异面直线.
微判断(1)没有公共点的两条直线是平行直线.( )(2)互相垂直的两条直线是相交直线.( )(3)既不平行又不相交的两条直线是异面直线.( )(4)不在同一平面内的两条直线是异面直线.( )答案:(1)× (2)× (3)√ (4)×
微练习1若空间两条直线a和b没有公共点,则a与b的位置关系是( ) A.共面B.平行C.异面D.平行或异面答案:D解析:若直线a和b共面,则由题意可知a∥b;若a和b不共面,则由题意可知a与b是异面直线.
微练习2一条直线与两条异面直线中的一条平行,则它和另一条的位置关系是( )A.平行或异面B.相交或异面C.异面 D.相交
在长方体ABCD-A1B1C1D1中,AA1与BC是异面直线,又AA1∥BB1,AA1∥DD1,显然BB1∩BC=B,DD1与BC是异面直线.
知识点三:空间中直线与平面、平面与平面的位置关系1.直线在平面内
不难看出,图中,点A,B确定的直线l上的所有点都在平面α内,这称为直线l在平面α内(或平面α过直线l),记作l⊂α.
2.直线在平面外直线m上至少有一个点不在平面α内,这称为直线m在平面α外,记作m⊄α;图中的m与α有且只有一个公共点(称为直线m与平面α相交),一般简写为m∩α=B.
3.直线与平面平行一般地,如果l是空间中的一条直线,α是空间中的一个平面,则l∩α≠⌀与l∩α=⌀有且只有一种情况成立.而且,当l∩α≠⌀时,要么l⊂α,要么l与α只有一个公共点;当l∩α=⌀时,称直线l与平面α平行,记作l∥α.
4.平面与平面相交如图α与β有公共点,这称为平面α与平面β相交,记作α∩β≠⌀.更进一步可以看出,一个点是α与β的公共点,当且仅当这个点在直线k上,这可记作α∩β=k.
5.平面与平面平行如果α与β是空间中的两个平面,则α∩β≠⌀与α∩β=⌀有且只有一种情况成立.而且,当α∩β≠⌀时,α与β的公共点组成一条直线;当α∩β=⌀时,称平面α与平面β平行,记作α∥β.
6.直线与平面的位置关系列表比较
7.两个平面的位置关系列表比较
名师点析 1.一般地,直线a在平面α内时,应把直线a画在表示平面α的平行四边形内,切勿画出边框外;直线a与平面α相交时,应画成直线a与平面α只有一个公共点,被平面α遮住的部分画成虚线或不画;直线a与平面α平行时,应画成直线a与表示平面α的平行四边形的一条边平行,并画在表示平面α的平行四边形外.2.画两个互相平行的平面时,要注意使表示平面的两个平行四边形的对应边平行,两个平行四边形上下放置.
微思考1“直线与平面不相交”与“直线与平面没有公共点”是相同的意义吗?提示:不是.前者包括直线与平面平行及直线在平面内这两种情况;而后者仅指直线与平面平行.微思考2分别位于两个平行平面内的两条直线有什么位置关系?提示:这两条直线没有公共点,故它们的位置关系是平行或异面.
微判断(1)若直线l上有无数个点不在平面α内,则l∥α.( )(2)如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行.( )(3)若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点.( )答案:(1)× (2)× (3)√
微练习1若M∈平面α,M∈平面β,则α与β的位置关系是( )A.平行B.相交C.异面D.不确定答案:B解析:因为M∈α,M∈β,所以α与β相交于过点M的一条直线.
微练习2空间三个平面如果每两个都相交,那么它们的交线有 条. 答案:1或3解析:空间三个平面两两相交,则有一条交线或三条交线,三条交线平行或相交于一点.
知识点四:直线与平面垂直1.直线与平面垂直的定义(1)文字语言:一般地,如果直线l与平面α相交于一点A,且对平面α内的任意一条过点A的直线m,都有l⊥m,则称直线l与平面α垂直(或l是平面α的一条垂线,α是直线l的一个垂面),记作l⊥α.其中,点A称为垂足.(2)图形语言:如图.
画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.(3)符号语言:任意m⊂α,都有l⊥m⇒l⊥α.
2.投影、点到平面的距离、直线到平面的距离、两平行平面之间的距离的定义给定空间中一个平面α及一个点A,过A可以作而且只可以作平面α的一条垂线.如果记垂足为B,则称B为A在平面α内的射影(也称为投影),线段AB为平面α的垂线段,AB的长为点A到平面α的距离.特别地,当直线与平面平行时,直线上任意一点到平面的距离称为这条直线到这个平面的距离;当平面与平面平行时,一个平面上任意一点到另一个平面的距离称为这两平行平面之间的距离.
微思考鲁班是我国古代一位出色的发明家,他在做木工时,常遇到有关直角的问题.虽然他手头有画直角的矩,但用起来很费事.于是,鲁班对矩进行改进,做成一把叫做曲尺的“L”形木尺.现在木工要检查一根木棒是否和板面垂直,只需用曲尺在不同的方向(但不是相反的方向)检查两次,如图.如果两次检查时,曲尺的两边都分别与木棒和板面密合,便可以判定木棒与板面垂直.
(1)用“L”形木尺检查一次能判定木棒与板面垂直吗?(1)提示:不能.(2)上述内容说明了直线与平面垂直的条件是什么?(2)提示:直线垂直于平面内的两条相交直线.(3)若直线垂直于平面内的无数条直线,则直线与平面垂直吗?(3)提示:不一定.
微练习直线l⊥平面α,直线m⊂α,则l与m不可能( ) A.平行B.相交C.异面D.垂直答案:A解析:∵直线l⊥平面α,∴l与α相交.∵m⊂α,∴l与m相交或异面,由直线与平面垂直的定义,可知l⊥m.故l与m不可能平行.
文字、图形、符号三种语言的转化例1用符号语言表示下列语句,并画出图形.(1)三个平面α,β,γ相交于一点P,且平面α与平面β交于PA,平面α与平面γ交于PB,平面β与平面γ交于PC;(2)平面ABD与平面BCD交于BD,平面ABC与平面ADC交于AC.
解:(1)符号语言表示:α∩β∩γ=P,α∩β=PA,α∩γ=PB,β∩γ=PC.图形表示:如图①所示.
(2)符号语言表示:平面ABD∩平面BCD=BD,平面ABC∩平面ADC=AC.图形表示:如图②所示.
反思感悟 学习几何问题,三种语言间的互相转化是一种基本技能.要注意符号语言的意义,如点与直线、点与平面间的位置关系只能用“∈”或“∉”,直线与平面间的位置关系只能用“⊂”或“⊄”.由图形语言表示点、线、面的位置关系时,要注意实线和虚线的区别.
变式训练 1(1)若点M在直线a上,a在平面α内,则M,a,α间的关系可记为 . (2)根据右图,填入相应的符号:A 平面ABC,A 平面BCD,BD 平面ABC,平面ABC∩平面ACD= . (3)根据下列条件画出图形:平面α∩平面β=MN,△ABC的三个顶点满足条件A∈MN,B∈α,B∉MN,C∈β,C∉MN.
答案:(1)M∈a,a⊂α,M∈α(2)∈ ∉ ⊄ AC(3)如图所示.
空间两条直线位置关系的判定例2已知三条直线a,b,c,a与b异面,b与c异面,则a与c有什么样的位置关系?并画图说明.
解:直线a与c的位置关系有三种情况.直线a与c可能平行,如图①;可能相交,如图②;可能异面,如图③.
反思感悟 判定两条直线位置关系的方法判定两条直线的位置关系时,若要判定直线平行或相交,可用平面几何中的定义和方法来处理;判定异面直线的方法往往根据连接平面内一点与平面外一点的直线和这个平面内不经过此点的直线是异面直线来判断.
变式训练 2 如图,在正方体ABCD-A1B1C1D1中,判断下列直线的位置关系:(1)直线A1B与直线D1C的位置关系是 ; (2)直线A1B与直线B1C的位置关系是 .
答案:(1)平行 (2)异面解析:(1)因为A1D1?B1C1,B1C1?BC,所以A1D1?BC,即四边形A1D1CB为平行四边形,所以A1B∥D1C.(2)因为直线A1B⊂平面A1B,B1∈平面A1B,且B1∉直线A1B,直线CB1⊄平面A1B,所以直线A1B与直线CB1为异面直线.
直线与平面的位置关系例3下列五个命题中正确命题的个数是( )①如果a,b是两条直线,a∥b,那么a平行于经过b的任何一个平面;②如果直线a和平面α满足a∥α,那么a与平面α内的任何一条直线平行;③如果直线a,b满足a∥α,b∥α,那么a∥b;④如果直线a,b和平面α满足a∥b,a∥α,b⊄α,那么b∥α;⑤如果a与平面α上的无数条直线平行,那么直线a必平行于平面α.A.0B.1C.2D.3
反思感悟 空间中直线与平面只有三种位置关系:直线在平面内、直线与平面相交、直线与平面平行.在判断直线与平面的位置关系时,这三种情况都要考虑到,避免遗漏.正方体(长方体)是立体几何中的重要模型,直线与平面的位置关系都可以在这个模型中得到反映,故我们可以把要判断位置关系的直线、平面放在正方体(长方体)中,以便正确作出判断,避免凭空臆断.
变式训练 3下列命题中的真命题是( )A.若点A∈α,点B∉α,则直线AB与平面α相交B.若a⊂α,b⊄α,则a与b必异面C.若点A∉α,点B∉α,则直线AB∥平面αD.若a∥α,b⊂α,则a∥b
答案:A解析:选项A正确.对于选项B,如图①显然错误.对于选项C,如图②显然错误.对于选项D,如图③显然错误.故选A.
两个平面的位置关系例4α,β是两个不重合的平面,下面说法正确的是( )A.平面α内有两条直线a,b都与平面β平行,那么α∥βB.平面α内有无数条直线平行于平面β,那么α∥βC.若直线a与平面α和平面β都平行,那么α∥βD.平面α内所有的直线都与平面β平行,那么α∥β
反思感悟 判断两平面之间的位置关系时,可把文字语言转化为图形语言,搞清图形间的相对位置是确定的还是可变的,借助于直观想象能力,确定平面间的位置关系.
变式训练 4如果在两个平面内分别有一条直线,这两条直线互相平行,那么两个平面的位置关系一定是( )A.平行B.相交 C.平行或相交D.不能确定答案:C解析:由题目分别在两个平面内的两直线平行判定两平面是相交或平行.解答本题可逆向考虑画两个平行面,看是否能在此两面内画两条平行线.同样画两相交面,看是否能在此两面内画两条平行线,再作出选择(如图所示).
直线和平面垂直的定义例5直线l与平面α内的无数条直线垂直,则直线l与平面α的关系是( )A.l和平面α平行B.l和平面α垂直C.l在平面α内 D.不能确定
答案:D解析:如图所示,直线l和平面α平行,或直线l和平面α垂直或直线l在平面α内都有可能.故选D.
反思感悟 直线和平面垂直的定义是描述性定义,对直线的任意性要注意理解.实际上,“任何一条”与“所有”表达相同的含义.当直线与平面垂直时,该直线就垂直于这个平面内的任何直线.由此可知,如果一条直线与一个平面内的一条直线不垂直,那么这条直线就一定不与这个平面垂直.
变式训练 5在长方体ABCD-A1B1C1D1中,不能作为平面ABCD垂线的是( )A.AA1B.BB1C.CC1D.AD1答案:D
线、面位置关系图形的画法典例作出下列各题的图形.(1)画直线a,b,使a∩α=A,b∥α.(2)画平面α,β,γ,使α∥β,γ∩α=m,γ∩β=n.
变式训练 在图中画出三个两两相交的平面.
1.若点Q在直线b上,b在平面β内,则Q,b,β之间的关系可记作( )A.Q∈b∈βB.Q∈b⊂βC.Q⊂b⊂βD.Q⊂b∈β答案:B解析:因为点Q(元素)在直线b(集合)上,所以Q∈b.又因为直线b(集合)在平面β(集合)内,所以b⊂β.所以Q∈b⊂β.
2.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一平面的位置关系为( )A.平行 B.相交C.直线在平面内D.平行或直线在平面内答案:D解析:由题知这条直线可能在另一平面内也可能与另一平面平行.
3.长方体的一条体对角线与长方体的棱所组成的异面直线有 对.
解析:如图所示,在长方体AC1中,与对角线AC1成异面直线的是:A1D1,BC,BB1,DD1,A1B1,DC,所以组成6对异面直线.
4.下列命题:①两个平面有无数个公共点,则这两个平面重合;②若l,m是异面直线,l∥α,m∥β,则α∥β.其中错误命题的序号为 .
答案:①②解析:对于①,两个平面相交,也有无数多个公共点,故①错误;对于②,借助于正方体ABCD-A1B1C1D1,AB∥平面DCC1D1,B1C1∥平面AA1D1D,又AB与B1C1异面,而平面DCC1D1与平面AA1D1D相交,故②错误.













