2021年山东省济宁市金乡县中考数学二模试卷

2021年山东省济宁市金乡县中考数学二模试卷

一、选择题（本题共计10小题，每题3分，共计30分）

1．计算﹣32的结果等于（　　）

A．9 B．﹣9 C．6 D．﹣6

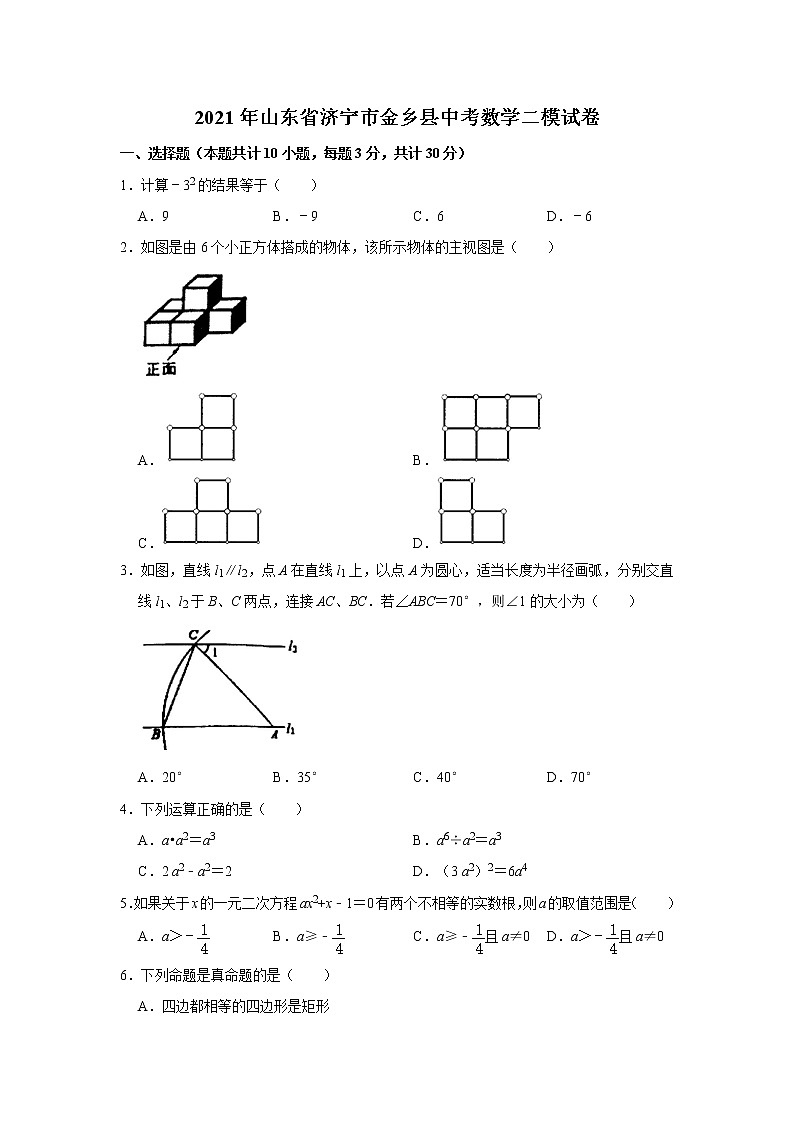
2．如图是由6个小正方体搭成的物体，该所示物体的主视图是（　　）

A． B． 

C． D．

3．如图，直线l1∥l2，点A在直线l1上，以点A为圆心，适当长度为半径画弧，分别交直线l1、l2于B、C两点，连接AC、BC．若∠ABC＝70°，则∠1的大小为（　　）

A．20° B．35° C．40° D．70°

4．下列运算正确的是（　　）

A．a•a2＝a3 B．a6÷a2＝a3 

C．2 a2﹣a2＝2 D．（3 a2）2＝6a4

5．如果关于x的一元二次方程ax2+x﹣1＝0有两个不相等的实数根，则a的取值范围是（　　）

A．a＞﹣ B．a≥﹣ C．a≥﹣且a≠0 D．a＞﹣且a≠0

6．下列命题是真命题的是（　　）

A．四边都相等的四边形是矩形 

B．菱形的对角线相等 

C．对角线互相垂直的平行四边形是正方形 

D．对角线相等的平行四边形是矩形

7．随着市场对新冠疫苗需求越来越大，为满足市场需求，某大型疫苗生产企业更新技术后，加快了生产速度，现在平均每天比更新技术前多生产10万份疫苗，现在生产500万份疫苗所需的时间与更新技术前生产400万份疫苗所需时间相同，设更新技术前每天生产x万份，依据题意得（　　）

A． B． 

C． D．

8．如图，在平面直角坐标系中，△ABC的顶点坐标分别是A（1，2），B（1，1），C（3，1），以原点为位似中心，在原点的同侧画△DEF，使△DEF与△ABC成位似图形，且相似比为2：1，则线段DF的长度为（　　）

A． B．2 C．4 D．2

9．按一定规律排列的一列数依次为：，按此规律排列下去，这列数中的第10个数是（　　）

A． B． C． D．

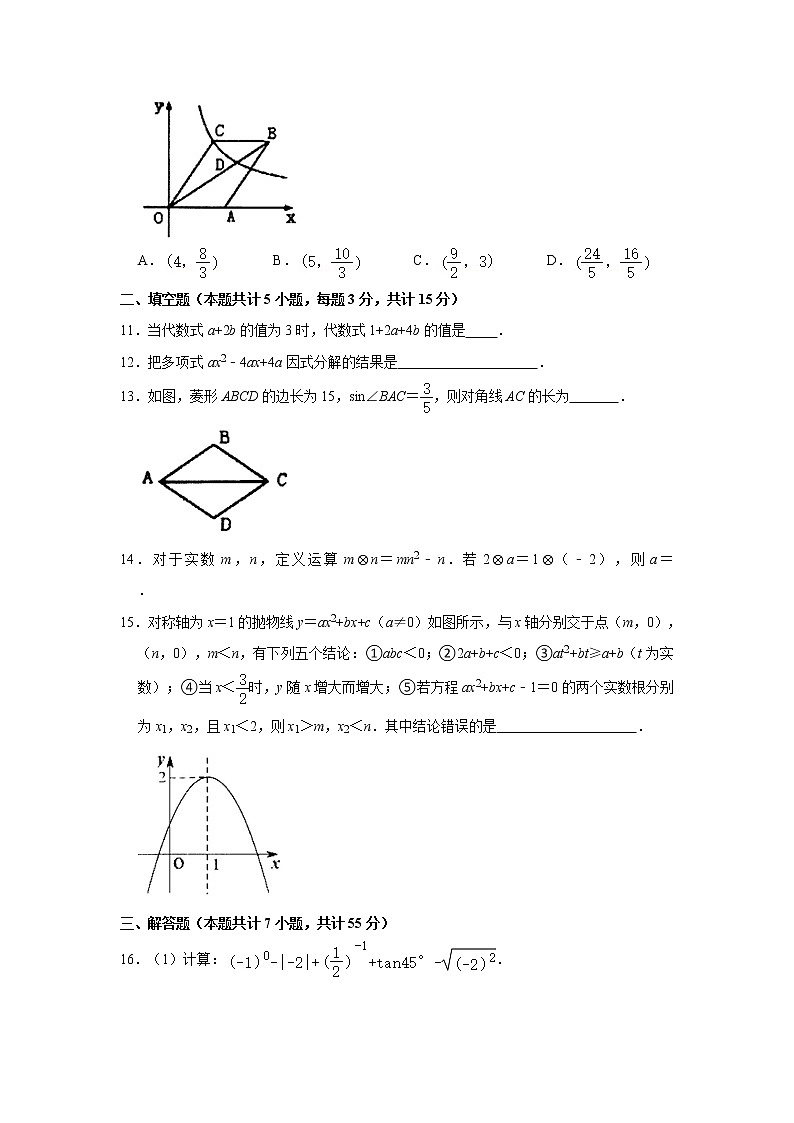
10．如图，平行四边形OABC的顶点A在x轴的正半轴上，点D（3，2）在对角线OB上，反比例函数y＝（k＞0，x＞0）的图象经过C、D两点．已知平行四边形OABC的面积是，则点B的坐标为（　　）

A． B． C． D．

二、填空题（本题共计5小题，每题3分，共计15分）

11．当代数式a+2b的值为3时，代数式1+2a+4b的值是　 　．

12．把多项式ax2﹣4ax+4a因式分解的结果是　                　．

13．如图，菱形ABCD的边长为15，sin∠BAC＝，则对角线AC的长为　   　．

14．对于实数m，n，定义运算m⨂n＝mn2﹣n．若2⨂a＝1⨂（﹣2），则a＝　                　．

15．对称轴为x＝1的抛物线y＝ax2+bx+c（a≠0）如图所示，与x轴分别交于点（m，0），（n，0），m＜n，有下列五个结论：①abc＜0；②2a+b+c＜0；③at2+bt≥a+b（t为实数）；④当x＜时，y随x增大而增大；⑤若方程ax2+bx+c﹣1＝0的两个实数根分别为x1，x2，且x1＜2，则x1＞m，x2＜n．其中结论错误的是　                　．

三、解答题（本题共计7小题，共计55分）

16．（1）计算：．

17．先化简，再求值：，其中a2﹣4＝0．

18．某校为了更好地开展球类运动，体育组决定用1600元购进足球8个和篮球14个，并且篮球的单价比足球的单价多20元，请解答下列问题：

（1）求出足球和篮球的单价；

（2）若学校欲用不超过3240元，且不少于3200元再次购进两种球50个，求出有哪几种购买方案？

（3）在（2）的条件下，若已知足球的进价为50元，篮球的进价为65元，则在第二次购买方案中，哪种方案商家获利最多？

19．中国式过马路，是网友对部分中国人集体闯红灯现象的一种调侃，即“凑够一撮人就可以走了，和红绿灯无关”，针对这种现象某媒体记者在多个路口采访闯红灯的行人，得出形成这种现象的四个基本原因：①马路红灯时间长，交通管理混乱占2%；②侥幸心态，只图自己节省时间；③对行人闯红灯违规行为惩罚措施不够严厉占8%；④从众心理．该记者将这次调查情况整理并绘制了如图尚不完整的统计图，请根据相关信息，解答下列问题．

（1）该记者本次一共调查了　 　名行人；

（2）求图1中②所在扇形的圆心角度数，并补全图2；

（3）在本次调查中，记者随机采访其中的一名行人，求这名行人属于第④种情况的概率．

20．济宁市内环高架桥的开通，较大程度缓解了市内交通的压力，最初设计南外环路口上桥匝道时，其坡角为15°，后来从安全角度考虑将匝道坡角改为5°（见示意图），如果高架桥高CD＝6米，匝道BD和AD每米造价均为4000元，那么设计优化后修建匝道AD的投资将增加多少元？（参考数据：sn5°≈0.08，sin15°≈0.25，tan5°≈0.09．tan15°≈0.27，结果保留整数）

21．如图，AB是⊙O的直径，点C是⊙O上一点，∠CAB的平分线AD交于点D，过点D作DE∥BC交AC的延长线于点E．

（1）求证：DE是⊙O的切线；

（2）过点D作DF⊥AB于点F，连接BD．若OF＝1，BF＝2，求sin∠DAB．

22．如图，二次函数y＝ax2+bx+4的图象与x轴交于点A（﹣1，0），B（4，0），与y轴交于点C，抛物线的顶点为D，其对称轴与线段BC交于点E．垂直于x轴的动直线l分别交抛物线和线段BC于点P和点F，动直线在抛物线的对称轴的右侧（不含对称轴）沿x轴正方向移动到B点．

（1）求二次函数y＝ax2+bx+4和BC所在直线的解析式；

（2）在动直线l移动的过程中，试求使四边形DEFP为平行四边形的点P的坐标；

（3）连接CP，CD，在移动直线l移动的过程中，抛物线上是否存在点P，使得以点P，C，F为顶点的三角形与△DCE相似，如果存在求出点P的坐标，如果不存在，请说明理由．