2021年甘肃省兰州市中考简答题练习（含答案）

这是一份2021年甘肃省兰州市中考简答题练习（含答案），共18页。试卷主要包含了÷，其中x＝+1，y＝﹣1，解不等式组，，并进行整理，得到下面部分信息等内容，欢迎下载使用。
2021年兰州市中考简答题练习
题号
一
总分
得分


一．解答题（共12小题，满分72分）
1．（4分）计算：（﹣）﹣1+2cos45°﹣|1﹣|+（3.14﹣π）0．
2．（4分）先化简，再求值：（﹣）÷，其中x＝+1，y＝﹣1．
3．（4分）解不等式组：并把解集在数轴上表示出来．
4．（5分）如图，在等腰三角形ABC中，AB＝AC＝8，AD是△ABC的角平分线，DE∥AC交AB于点 E．
（1）证明：AE＝ED；
（2）求线段DE的长．


5．（5分）某市为改善农村生活条件，满足居民清洁能源的需求，计划修建A、B两种型号的沼气池共24个，两种沼气池的修建费用、可供使用户数、占地面积如下表：
沼气池
修建费用（万元/个）
可供使用户数（户/个）
占地面积（平方米/个）
A型
3
20
10
B型
2
15
8
设修建A型沼气池x个，修建两种沼气池共需费用y万元．
（1）求y与x之间的函数关系式；
（2）若此次修建沼气池至少要保证幸福村400户的居民每户一个，且政府土地部门只批给该村沼气池用地220平方米，求出费用最少时的修建方案，并计算此时修建完沼气池剩余的用地面积．
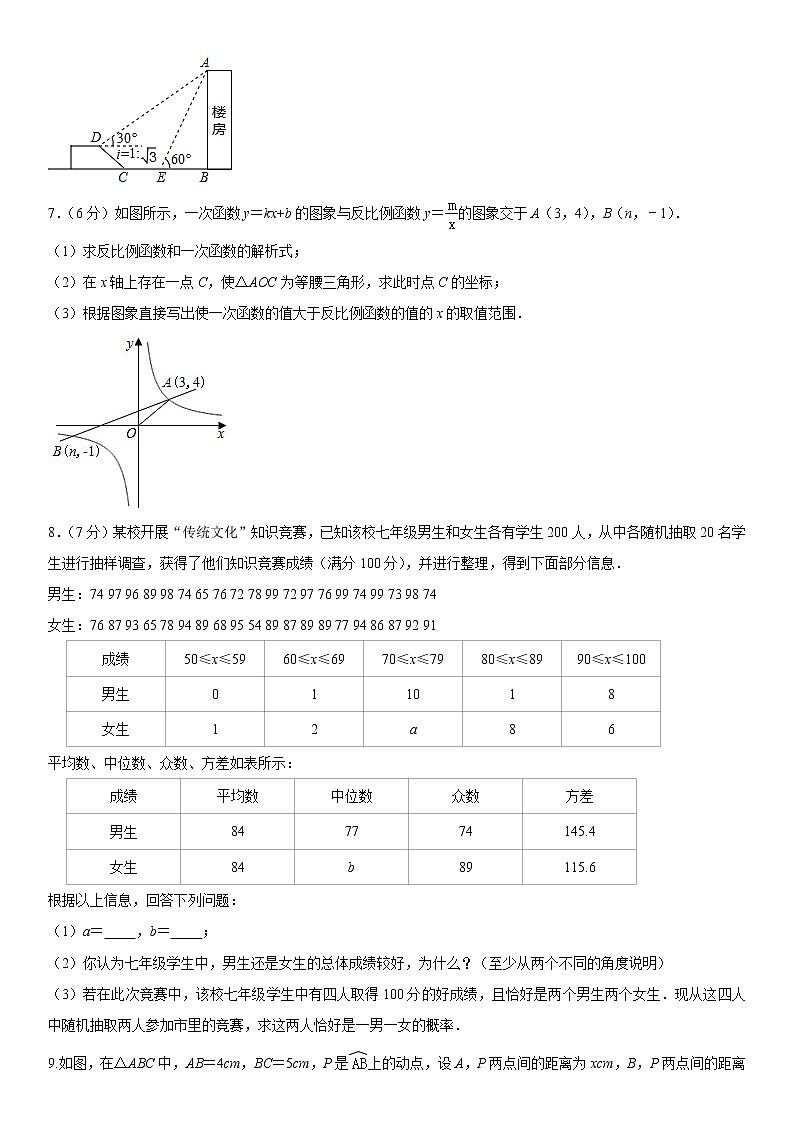
6．（6分）如图，在一次综合实践活动中，小亮要测量一楼房的高度，先在坡面D处测得楼房顶部A的仰角为30°，沿坡面向下走到坡脚C处，然后向楼房方向继续行走10米到达E处，测得楼房顶部A的仰角为60°．已知坡面CD＝10米，山坡的坡度i＝1：（坡度i是指坡面的铅直高度与水平宽度的比），求楼房AB高度．（结果精确到0.1米）（参考数据：≈1.73，≈1.41）

7．（6分）如图所示，一次函数y＝kx+b的图象与反比例函数y＝的图象交于A（3，4），B（n，﹣1）．
（1）求反比例函数和一次函数的解析式；
（2）在x轴上存在一点C，使△AOC为等腰三角形，求此时点C的坐标；
（3）根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围．

8．（7分）某校开展“传统文化”知识竞赛，已知该校七年级男生和女生各有学生200人，从中各随机抽取20名学生进行抽样调查，获得了他们知识竞赛成绩（满分100分），并进行整理，得到下面部分信息．
男生：74 97 96 89 98 74 65 76 72 78 99 72 97 76 99 74 99 73 98 74
女生：76 87 93 65 78 94 89 68 95 54 89 87 89 89 77 94 86 87 92 91
成绩
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
男生
0
1
10
1
8
女生
1
2
a
8
6
平均数、中位数、众数、方差如表所示：
成绩
平均数
中位数
众数
方差
男生
84
77
74
145.4
女生
84
b
89
115.6
根据以上信息，回答下列问题：
（1）a＝　 　，b＝　 　；
（2）你认为七年级学生中，男生还是女生的总体成绩较好，为什么？（至少从两个不同的角度说明）
（3）若在此次竞赛中，该校七年级学生中有四人取得100分的好成绩，且恰好是两个男生两个女生．现从这四人中随机抽取两人参加市里的竞赛，求这两人恰好是一男一女的概率．
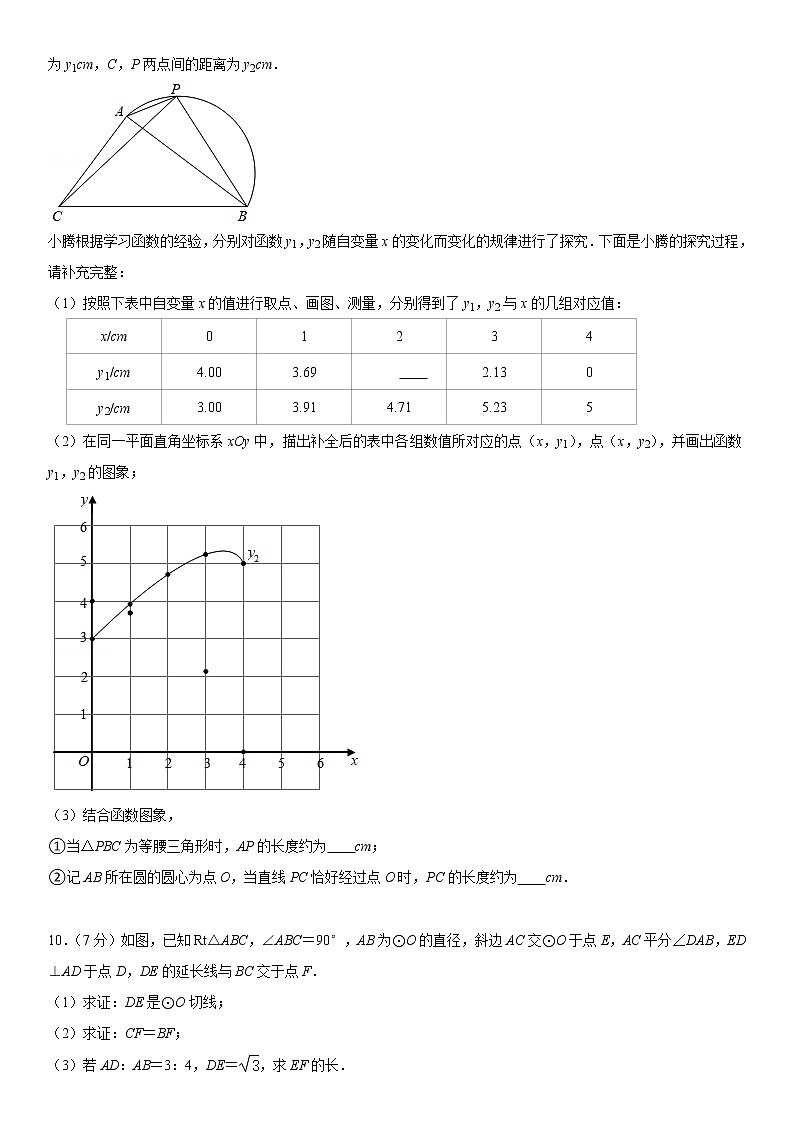
9.如图，在△ABC中，AB＝4cm，BC＝5cm，P是上的动点，设A，P两点间的距离为xcm，B，P两点间的距离为y1cm，C，P两点间的距离为y2cm．

小腾根据学习函数的经验，分别对函数y1，y2随自变量x的变化而变化的规律进行了探究．下面是小腾的探究过程，请补充完整：
（1）按照下表中自变量x的值进行取点、画图、测量，分别得到了y1，y2与x的几组对应值：
x/cm
0
1
2
3
4
y1/cm
4.00
3.69
　　
2.13
0
y2/cm
3.00
3.91
4.71
5.23
5
（2）在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点（x，y1），点（x，y2），并画出函数y1，y2的图象；

（3）结合函数图象，
①当△PBC为等腰三角形时，AP的长度约为　　cm；
②记AB所在圆的圆心为点O，当直线PC恰好经过点O时，PC的长度约为　　cm．

10．（7分）如图，已知Rt△ABC，∠ABC＝90°，AB为⊙O的直径，斜边AC交⊙O于点E，AC平分∠DAB，ED⊥AD于点D，DE的延长线与BC交于点F．
（1）求证：DE是⊙O切线；
（2）求证：CF＝BF；
（3）若AD：AB＝3：4，DE＝，求EF的长．

11．（8分）如图，在平行四边形ABCD中，按下列步骤作图：
①以点B为圆心，以适当长为半径作弧，交AB于点N．交BC于点M；
②再分别以点M和点N为圆心，大于MN的长为半径作弧，两弧交于点G；
③作射线BG交AD于F；
④过点A作AE⊥BF交BF于点P，交BC于点E；
⑤连接EF，PD．
（1）求证：四边形ABEF是菱形；
（2）若AB＝8，AD＝10，∠ABC＝60°，求DP的长．

12．（9分）如图1，在平面直角坐标系中，一次函数y＝x﹣2的图象与x轴交于点B，与y轴交于点C，抛物线y＝x2+bx+c的图象经过B、C两点，且与x轴的负半轴交于点A．
（1）求二次函数的表达式；
（2）若点D在直线BC下方的抛物线上，如图1，连接DC、DB，设四边形OCDB的面积为S，求S的最大值；
（3）若点D在抛物线上，如图2，过点D作DM⊥BC于点M，试问是否存在点D，使得△CDM中的某个角恰好等于∠ABC？若存在，请求点D的横坐标；若不存在，请说明理由．


2021年兰州市中考简答题练习（答案）
一．解答题（共11小题，满分65分）
1．（4分）计算：（﹣）﹣1+2cos45°﹣|1﹣|+（3.14﹣π）0．
【解答】解：原式＝﹣4+2×﹣（﹣1）+1
＝﹣4+﹣+1+1
＝﹣2．
2．（4分）先化简，再求值：（﹣）÷，其中x＝+1，y＝﹣1．
【解答】解：（﹣）÷，
＝[﹣]÷，
＝×，
＝，
当x＝+1，y＝﹣1时，
原式＝＝2﹣．
3．（4分）解不等式组：并把解集在数轴上表示出来．
【解答】解：解不等式①，得：x＞﹣4，
解不等式②，得：x≤0，
则不等式组的解集为﹣4＜x≤0，
将解集表示在数轴上如下：

4．（5分）如图，在等腰三角形ABC中，AB＝AC＝8，AD是△ABC的角平分线，DE∥AC交AB于点 E．
（1）证明：AE＝ED；
（2）求线段DE的长．

【解答】解：（1）∵AD平分∠BAC，
∴∠EAD＝∠CAD，
∵DE∥AC，
∴∠ADE＝∠CAD，
∴∠EAD＝∠ADE．
∴AE＝DE．
（2）∵DE∥AC，
∴∠EDB＝∠C．
∵AB＝AC，
∴∠B＝∠C，
∴∠EDB＝∠B．
∴BE＝DE，
∴DE＝BE＝AE＝＝×8＝4．
5．（5分）某市为改善农村生活条件，满足居民清洁能源的需求，计划修建A、B两种型号的沼气池共24个，两种沼气池的修建费用、可供使用户数、占地面积如下表：
沼气池
修建费用（万元/个）
可供使用户数（户/个）
占地面积（平方米/个）
A型
3
20
10
B型
2
15
8
设修建A型沼气池x个，修建两种沼气池共需费用y万元．
（1）求y与x之间的函数关系式；
（2）若此次修建沼气池至少要保证幸福村400户的居民每户一个，且政府土地部门只批给该村沼气池用地220平方米，求出费用最少时的修建方案，并计算此时修建完沼气池剩余的用地面积．
【解答】解：（1）由题意可得，
y＝3x+2（24﹣x）＝x+48，
即y与x的函数关系式为y＝x+48；
（2）∵政府土地部门只批给该村沼气池用地220平方米，且修建沼气池至少要保证幸福村400户的居民每户一个，
∴，
解得8≤x≤14，
∵x为整数，
∴x＝8，9，10，11，12，13，14．
即有7种满足上述要求的修建方案：
①修A型池8个，B型池16个；
②修A型池9个，B型池15个；
③修A型池10个，B型池14个；
④修A型池11个，B型池13个；
⑤修A型池12个，B型池12个；
⑥修A型池13个，B型池11个；
⑦修A型池14个，B型池10个；
∵修建费为：y＝x+48，
∴当x有最小值时，y有最小值，
即费用最少时的方案为A型池修8个，B型池16个，
故剩余用地面积为：220﹣8×10﹣16×8＝12（m2）．
6．（6分）如图，在一次综合实践活动中，小亮要测量一楼房的高度，先在坡面D处测得楼房顶部A的仰角为30°，沿坡面向下走到坡脚C处，然后向楼房方向继续行走10米到达E处，测得楼房顶部A的仰角为60°．已知坡面CD＝10米，山坡的坡度i＝1：（坡度i是指坡面的铅直高度与水平宽度的比），求楼房AB高度．（结果精确到0.1米）（参考数据：≈1.73，≈1.41）

【解答】解：过D作DG⊥BC于G，DH⊥AB于H，交AE于F，作FP⊥BC于P，如图所示：
则DG＝FP＝BH，DF＝GP，
∵坡面CD＝10米，山坡的坡度i＝1：，
∴∠DCG＝30°，
∴FP＝DG＝CD＝5，
∴CG＝DG＝5，
∵∠FEP＝60°，
∴FP＝EP＝5，
∴EP＝，
∴DF＝GP＝5+10+＝+10，
∵∠AEB＝60°，
∴∠EAB＝30°，
∵∠ADH＝30°，
∴∠DAH＝60°，
∴∠DAF＝30°＝∠ADF，
∴AF＝DF＝+10，
∴FH＝AF＝+5，
∴AH＝FH＝10+5，
∴AB＝AH+BH＝10+5+5＝15+5≈15+5×1.73≈23.7（米），
答：楼房AB高度约为23.7米．

7．（6分）如图所示，一次函数y＝kx+b的图象与反比例函数y＝的图象交于A（3，4），B（n，﹣1）．
（1）求反比例函数和一次函数的解析式；
（2）在x轴上存在一点C，使△AOC为等腰三角形，求此时点C的坐标；
（3）根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围．

【解答】解：（1）把A（3，4）代入，
∴m＝12，
∴反比例函数的解析式是；
把B（n，﹣1）代入得n＝﹣12．
把A（3，4）、B（﹣12，﹣1）分别代入y＝kx+b中，
得，
解得，
∴一次函数的解析式为；

（2）∵A（3，4），
∴OA＝，
∵△AOC为等腰三角形，
分三种情况：
①当OA＝OC时，OC＝5，
此时点C的坐标为（5，0），（﹣5，0）；
②当AO＝AC时，∵A（3，4），点C和点O关于过A点且垂直于x轴的直线对称，
此时点C的坐标为（6，0）；
③当CA＝CO时，点C在线段OA的垂直平分线上，
过A作AD⊥x轴，垂足为D，
由题意可得：OD＝3，AD＝4，AO＝5，设OC＝x，则AC＝x，
在△ACD中，42+（x﹣3）2＝x2，
解得：x＝，
此时点C的坐标为；
解法二：提示：设OA的垂直平分线交OA于M，证明△OMC∽△ODA，利用相似三角形的性质求解．


综上：点C的坐标为：（6，0），（5，0），，（﹣5，0）；

（3）由图得：
当一次函数图象在反比例函数图象上方时，
﹣12＜x＜0或x＞3，
即使一次函数的值大于反比例函数的值的x的取值范围是：﹣12＜x＜0或x＞3．
8．（7分）某校开展“传统文化”知识竞赛，已知该校七年级男生和女生各有学生200人，从中各随机抽取20名学生进行抽样调查，获得了他们知识竞赛成绩（满分100分），并进行整理，得到下面部分信息．
男生：74 97 96 89 98 74 65 76 72 78 99 72 97 76 99 74 99 73 98 74
女生：76 87 93 65 78 94 89 68 95 54 89 87 89 89 77 94 86 87 92 91
成绩
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
男生
0
1
10
1
8
女生
1
2
a
8
6
平均数、中位数、众数、方差如表所示：
成绩
平均数
中位数
众数
方差
男生
84
77
74
145.4
女生
84
b
89
115.6
根据以上信息，回答下列问题：
（1）a＝　3　，b＝　88　；
（2）你认为七年级学生中，男生还是女生的总体成绩较好，为什么？（至少从两个不同的角度说明）
（3）若在此次竞赛中，该校七年级学生中有四人取得100分的好成绩，且恰好是两个男生两个女生．现从这四人中随机抽取两人参加市里的竞赛，求这两人恰好是一男一女的概率．
【解答】解：（1）由题意a＝3，b＝＝88，
故答案为：3，88．

（2）从中位数看：女生的成绩比男生的成绩好，
从众数看：女生的成绩比男生的成绩好，
从方差看：女生的方差比男生的方差小，成绩比较稳定．
综上所述，女生的成绩比较好．

（2）画树状图如下：

所有等可能的情况有12种，其中一男一女有8种，
则P＝＝．
9.（7分）如图，在△ABC中，AB＝4cm，BC＝5cm，P是上的动点，设A，P两点间的距离为xcm，B，P两点间的距离为y1cm，C，P两点间的距离为y2cm．

小腾根据学习函数的经验，分别对函数y1，y2随自变量x的变化而变化的规律进行了探究．下面是小腾的探究过程，请补充完整：
（1）按照下表中自变量x的值进行取点、画图、测量，分别得到了y1，y2与x的几组对应值：
x/cm
0
1
2
3
4
y1/cm
4.00
3.69
　　
2.13
0
y2/cm
3.00
3.91
4.71
5.23
5
（2）在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点（x，y1），点（x，y2），并画出函数y1，y2的图象；

（3）结合函数图象，
①当△PBC为等腰三角形时，AP的长度约为　　cm；
②记AB所在圆的圆心为点O，当直线PC恰好经过点O时，PC的长度约为　　cm．

【解答】解：（1）由画图可得，x＝2时，y1≈3.09cm（答案不唯一）．
故答案为：3.09（答案不唯一）．

（2）描点绘图如下：


（3）①由y1与y2的交点的横坐标可知，x≈0.83cm时，PC＝PB，
当x≈2.49cm时，y2＝5cm，即PC＝BC，
观察图象可知，PB不可能等于BC，
故答案为：0.83或2.49（答案不唯一）．
②当直线PC恰好经过点O时，PC的长度取得最大值，从图象看，PC＝y2≈5.32cm，
故答案为5.32（答案不唯一）．

10．（7分）如图，已知Rt△ABC，∠ABC＝90°，AB为⊙O的直径，斜边AC交⊙O于点E，AC平分∠DAB，ED⊥AD于点D，DE的延长线与BC交于点F．
（1）求证：DE是⊙O切线；
（2）求证：CF＝BF；
（3）若AD：AB＝3：4，DE＝，求EF的长．

【解答】解：（1）连接OE，

∵AC平分∠DAB，
∴∠DAE＝∠OAE，
∵OA＝OE，
∴∠OAE＝∠OEA，
∴∠DAE＝∠OEA，
∴AD∥OE，
∵AD⊥ED，
∴OE⊥DE，
∵点E在⊙O上，
∴DE是⊙O的切线；
（2）连接BE，

∵AB为⊙O的直径，
∴∠AEB＝90°＝∠BEC，
∵∠ABC＝90°，AB为⊙O的直径，
∴FB为⊙O的切线，
又∵DE是⊙O的切线，
∴FE＝FB，
∴∠FEB＝∠FBE，
∵∠FEB+∠FEC＝90°＝∠FBE+∠C，
∴∠FEC＝∠C，
∴FE＝FC，
又∵FE＝FB，
∴FB＝FC；
（3）∵∠ADE＝∠ABC＝90°，∠DAE＝∠CAB，
∴△ADE～△ABC，
∴，
∵DE＝，
∴BC＝，
∵FE＝FC＝FB＝BC，
∴EF＝．
11．（8分）如图，在平行四边形ABCD中，按下列步骤作图：
①以点B为圆心，以适当长为半径作弧，交AB于点N．交BC于点M；
②再分别以点M和点N为圆心，大于MN的长为半径作弧，两弧交于点G；
③作射线BG交AD于F；
④过点A作AE⊥BF交BF于点P，交BC于点E；
⑤连接EF，PD．
（1）求证：四边形ABEF是菱形；
（2）若AB＝8，AD＝10，∠ABC＝60°，求DP的长．

【解答】（1）证明：由作图知BA＝BE，∠ABF＝∠EBF，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠EBF＝∠AFB，
∴∠ABF＝∠AFB，
∴AB＝AF＝BE，
∴四边形ABEF是平行四边形，
又AB＝BE，
∴四边形ABEF是菱形；

（2）解：作PH⊥AD于H，






∵四边形ABEF是菱形，∠ABC＝60°，AB＝8，
∴AB＝AF＝8，∠ABF＝∠AFB＝30°，AP⊥BF，
∴AP＝AB＝4，
∴PH＝2，DH＝8，
∴DP＝＝＝2．
12．（9分）如图1，在平面直角坐标系中，一次函数y＝x﹣2的图象与x轴交于点B，与y轴交于点C，抛物线y＝x2+bx+c的图象经过B、C两点，且与x轴的负半轴交于点A．
（1）求二次函数的表达式；
（2）若点D在直线BC下方的抛物线上，如图1，连接DC、DB，设四边形OCDB的面积为S，求S的最大值；
（3）若点D在抛物线上，如图2，过点D作DM⊥BC于点M，试问是否存在点D，使得△CDM中的某个角恰好等于∠ABC？若存在，请求点D的横坐标；若不存在，请说明理由．

【解答】解：（1）对于y＝x﹣2，令y＝x﹣2＝0，解得x＝4，令x＝0，则y＝﹣2，
故点B、C的坐标分别为（4，0）、（0，﹣2）；
将点B、C的坐标代入抛物线表达式得，解得，
故抛物线的表达式为y＝x2﹣x﹣2①；

（2）连接OD，点D的坐标为（x，x2﹣x﹣2），

则S＝S△ODC+S△ODB＝×OC×xD+×BO×（﹣yD）＝×2×x+×4×（x2﹣x﹣2）＝﹣x2+4x+4，
∵﹣1＜0，故S有最大值，
当x＝2时，S有最大值8；

（3）存在，理由：
①当∠DCM＝∠ABC时，
当点M在线段BC时，如题干图2，
则CD∥OB，
∵抛物线的对称轴为直线x＝，
则根据函数的对称性点D、C关于抛物线对称轴对称，故点D的坐标为（3，﹣2）；
当点M在CB的延长线时，如图2，

∵∠DCM＝∠ABC，
故TB＝TC，
设TB＝x＝CT，则OT＝4﹣t，
在Rt△OTC中，CT2＝OT2+OC2，即t2＝（4﹣t）2+22，解得t＝2.5，
故点T的坐标为（，0），
由点C、T的坐标得，直线CT的表达式为y＝x﹣2②，
联立①②并解得x＝0（舍去）或；
故点D的横坐标为3或；
②当∠MDC＝ABC时，如图3，

过点D作x轴的平行线交BC于点Q，交y轴于点P，
则∠Q＝∠ABC，
∵∠MDC＝ABC，
∴△DMC∽△BOC，
则，
故设MD＝2k，则CM＝k，CD＝k，
在Rt△MAD中，tan∠Q＝tan∠ABC＝，则QM＝4k，
则CQ＝3k，DQ＝＝2k，
在Rt△PQC中，tanQ＝，则sinQ＝，cosQ＝，
则CP＝CQsinQ＝k，同理可得PQ＝k，
则PD＝DQ﹣PQ＝2k﹣k＝k，
设点D的坐标为（x，x2﹣x﹣2），则DP＝x，CP＝﹣x2+x，
∴＝，解得x＝0（舍去）或1.5，
故点D的横坐标为1.5；
综上，点D的横坐标为1.5或3或．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布