2021年广西柳州市中考模拟复习试卷八（含答案）

这是一份2021年广西柳州市中考模拟复习试卷八（含答案），共9页。试卷主要包含了选择题，填空题，解答题，综合题等内容，欢迎下载使用。

检验4个工件，其中超过标准质量的克数记作正数，不足标准质量的克数记作负数．从轻重的角度看，最接近标准的工件是（ ）
A.﹣2 B.﹣3 C.3 D.5
小明上网查德H7N9禽流感病毒直径约为0.00000008米，用科学计数法表示为（ ）
A.0.8×10-7米 B.8×10-7米 C.8×10-8米 D.8×10-9米
下列图形中，既是轴对称图形又是中心对称图形的是（ ）

下面所给几何体的俯视图是（ ）
A. B. C. D.
已知直线m∥n，将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°)，
其中A，B两点分别落在直线m，n上，若∠1=40°，则∠2的度数为( )
A．10° B．20° C．30° D．40°
已知一组数据：9，8，8，6，9，5，7，则这组数据的中位数是（ ）
A．6B．7C．8D．9
已知一次函数y=kx＋b-x的图象与x轴的正半轴相交，且函数值y随自变量x的增大而增大，则k，b的取值情况为( )
A.k＞1，b＜0 B.k＞1，b＞0 C.k＞0，b＞0 D.k＞0，b＜0
三角形两边长为6与8，那么周长L的取值范围（ ）
A．2 如果(x﹣2)(x+1)=x2+mx+n,那么m+n的值为（ ）
A.﹣1 B.1 C.﹣3 D.3
如图，AB是⊙O的直径，点C、D在⊙O上.若∠ACD=25°，则∠BOD的度数为（ ）
A.100° B.120° C.130° D.150°
下列计算正确的是 ( )
A. B. C. D.
如图，二次函数y=ax2+bx+c（a≠0）的图象经过点（﹣1，2），且与x轴交点的横坐标分别为x1，x2，其中﹣2＜x1＜﹣1，0＜x2＜1.
下列结论：①4a﹣2b+c＜0；②2a﹣b＜0；③a＜0；④b2+8a＞4ac，其中正确的有（ ）
A.1个 B.2个 C.3个 D.4个
二、填空题（本大题共6小题，每小题3分，共18分）
分解因式：a3﹣25a= .
一个不透明的袋中装有除颜色外均相同的9个红球，3个白球，若干个绿球，每次摇匀后随机摸出一个球，记下颜色后再放回袋中，经过大量重复实验后，发现摸到绿球的频率稳定在0.2，则袋中约有绿球 个.
如图，A、B是曲线y=上的点，经过A、B两点向x轴、y轴作垂线段，若S阴影=1，则S1＋S2_______．
如果方程x2﹣（m﹣1）x+=0有两个相等的实数根，则m的值为
如图,在扇形中,∠AOB=900,,C是弧AB上一点,且CD⊥OB,CE⊥OA,垂足分别为点D、E,软弱BD=1，OD=3，则DE= ．

如图，正方形ABCD的边长为12，点E在边AB上，BE=8，过点E作EF∥BC，分别交BD、CD于G、F两点.若点P、Q分别为DG、CE的中点，则PQ的长为 .
三、解答题（本大题共6小题，共54分）
先化简，再求值：(a﹣9+)÷(a﹣1﹣)，其中a=．
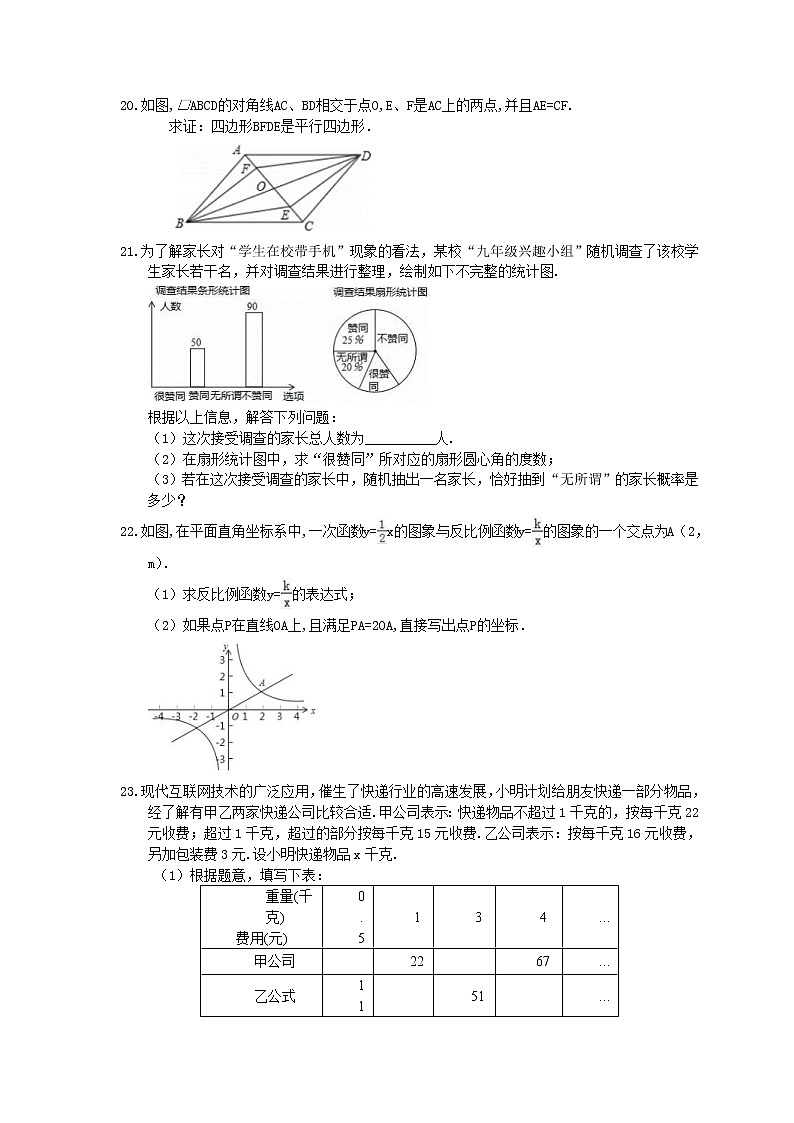
如图,□ABCD的对角线AC、BD相交于点O,E、F是AC上的两点,并且AE=CF.
求证：四边形BFDE是平行四边形．

为了解家长对“学生在校带手机”现象的看法，某校“九年级兴趣小组”随机调查了该校学生家长若干名，并对调查结果进行整理，绘制如下不完整的统计图.
根据以上信息，解答下列问题：
（1）这次接受调查的家长总人数为__________人.
（2）在扇形统计图中，求“很赞同”所对应的扇形圆心角的度数；
（3）若在这次接受调查的家长中，随机抽出一名家长，恰好抽到“无所谓”的家长概率是多少？
如图,在平面直角坐标系中,一次函数y=x的图象与反比例函数y=的图象的一个交点为A（2，m）．
（1）求反比例函数y=的表达式；
（2）如果点P在直线OA上,且满足PA=2OA,直接写出点P的坐标．
现代互联网技术的广泛应用，催生了快递行业的高速发展，小明计划给朋友快递一部分物品，经了解有甲乙两家快递公司比较合适.甲公司表示：快递物品不超过1千克的，按每千克22元收费；超过1千克，超过的部分按每千克15元收费.乙公司表示：按每千克16元收费，另加包装费3元.设小明快递物品x千克.
（1）根据题意，填写下表：

（2）请分别写出甲乙两家快递公司快递该物品的费用y（元）与x（千克）之间的函数关系式；
（3）小明应选择哪家快递公司更省钱？
如图，⊙O的直径DF与弦AB交于点E，C为⊙O外一点，CB⊥AB，G是直线CD上一点，
∠ADG=∠ABD．
求证：AD•CE=DE•DF；
说明：（1）如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路过程写出来（要求至少写3步）；
（2）在你经历说明（1）的过程之后，可以从下列①、②、③中选取一个补充或更换已知条件，完成你的证明．
①∠CDB=∠CEB；②AD∥EC；③∠DEC=∠ADF，且∠CDE=90°．
四、综合题（本大题共1小题，共12分）
如图，在平面直角坐标系中，平行四边形OABC的顶点A，C的坐标分别为(6，0)，(4，3)，经过B，C两点的抛物线与x轴的一个交点D的坐标为(1，0)．
(1)求该抛物线的解析式；
(2)若∠AOC的平分线交BC于点E，交抛物线的对称轴于点F，点P是x轴上一动点，当PE+PF的值最小时，求点P的坐标；
(3)在(2)的条件下，过点A作OE的垂线交BC于点H，点M，N分别为抛物线及其对称轴上的动点，是否存在这样的点M，N，使得以点M，N，H，E为顶点的四边形为平行四边形？若存在，直接写出点M的坐标，若不存在，说明理由．
\s 0 参考答案
答案为：A
C
B
B
答案为：B.
答案为：C．
A
B
答案为：D.
答案为：C
答案为：C
D
解析：二次函数y=ax2+bx+c（a≠0）的图象经过点（﹣1，2），与y轴交于（0，2）点，且与x轴交点的横坐标分别为x1、x2，其中﹣2＜x1＜﹣1，0＜x2＜1，下列结论
①4a﹣2b+c＜0；当x=﹣2时，y=ax2+bx+c，y=4a﹣2b+c，
∵﹣2＜x1＜﹣1，∴y＜0，故①正确；
②2a﹣b＜0；
∵二次函数y=ax2+bx+c（a≠0）的图象经过点（﹣1，2），
∴a﹣b+c=2，与y轴交于（0，1）点，c=1，
∴a﹣b=1，二次函数的开口向下，a＜0，
又﹣1＜﹣＜0，∴2a﹣b＜0，故②正确；
③因为抛物线的开口方向向下，所以a＜0，故③正确；
④由于抛物线的对称轴大于﹣1，所以抛物线的顶点纵坐标应该大于2，即＞2，
由于a＜0，所以4ac﹣b2＜8a，即b2+8a＞4ac，故④正确，
故选：D.
答案为：a(a+5)(a﹣5).
答案为：3
答案为：4
答案为：m=2或m=0．
答案为：4；
答案为：2.
解：作QM⊥EF于点M，作PN⊥EF于点N，作QH⊥PN交PN的延长线于点H，如右图所示，
∵正方形ABCD的边长为12，BE=8，EF∥BC，点P、Q分别为DG、CE的中点，
∴DF=4，CF=8，EF=12，∴MQ=4，PN=2，MF=6，
∵QM⊥EF，PN⊥EF，BE=8，DF=4，∴△EGB∽△FGD，
∴，即，解得，FG=4，
∴FN=2，∴MN=6﹣2=4，∴QH=4，
∵PH=PN+QM，∴PH=6，∴PQ==，
故答案为：2.
解：
原式=÷=•=，
当a=时，原式==1﹣2．
证明：∵□ABCD的对角线AC、BD相交于点O，E、F是AC上的两点，
∴AO=CO，BO=DO，∵AE=CF，∴AF=EC，则FO=EO，∴四边形BFDE是平行四边形．
解：（1）这次接受调查的家长总人数为200人，故答案为：200；
（2）∵ “无所谓”的人数为40人，
“很赞同”的人数为20人，
则“很赞同”所对应的扇形圆心角的度数为36°；
（3）∵在所抽取的200人中，表示“无所谓”的人数为40，
恰好抽到“无所谓”的家长概率是0.2.
解：（1）∵一次函数y=x的图象与反比例函数y=的图象的一个交点为A（2，m），
∴点A（2，m）在一次函数y=x的图象上，∴m=×2=1，∴点A的坐标为（2，1）．
∵点A（2，1）在反比例函数y=图象上，∴1=，解得：k=2．∴反比例函数表达式为y=．
（2）∵点P在直线OA上，∴设点P的坐标为（2n，n）．∴点A的坐标为（2，1），
∴OA==，PA=．∵PA=2OA，即=2，
解得：n1=﹣1，n2=3．∴点P的坐标为（﹣2，﹣1）和（6，3）．

（1）证明：连接AF，
∵DF是⊙O的直径，
∴∠DAF=90°，
∴∠F+∠ADF=90°，
∵∠F=∠ABD，∠ADG=∠ABD，
∴∠F=∠ADG，
∴∠ADF+∠ADG=90°
∴直线CD是⊙O的切线
∴∠EDC=90°，
∴∠EDC=∠DAF=90°；
（2）选取①完成证明
证明：∵直线CD是⊙O的切线，
∴∠CDB=∠A．
∵∠CDB=∠CEB，
∴∠A=∠CEB．
∴AD∥EC．
∴∠DEC=∠ADF．
∵∠EDC=∠DAF=90°，
∴△ADF∽△DEC．
∴AD：DE=DF：EC．
∴AD•CE=DE•DF．
解：
(1)∵平行四边形OABC中，A(6，0)，C(4，3)
∴BC=OA=6，BC∥x轴
∴xB=xC+6=10，yB=yC=3，即B(10，3)
设抛物线y=ax2+bx+c经过点B、C、D(1，0)
∴ 解得：
∴抛物线解析式为y=﹣x2+x﹣
(2)如图1，作点E关于x轴的对称点E'，连接E'F交x轴于点P
∵C(4，3)∴OC=∵BC∥OA∴∠OEC=∠AOE
∵OE平分∠AOC∴∠AOE=∠COE∴∠OEC=∠COE∴CE=OC=5
∴xE=xC+5=9，即E(9，3)∴直线OE解析式为y=x
∵直线OE交抛物线对称轴于点F，对称轴为直线：x=﹣7∴F(7，)
∵点E与点E'关于x轴对称，点P在x轴上∴E'(9，﹣3)，PE=PE'
∴当点F、P、E'在同一直线上时，PE+PF=PE'+PF=FE'最小
设直线E'F解析式为y=kx+h
∴ 解得：∴直线E'F：y=﹣x+21
当﹣x+21=0时，解得：x=
∴当PE+PF的值最小时，点P坐标为(，0)．
(3)存在满足条件的点M，N，使得以点M，N，H，E为顶点的四边形为平行四边形．
设AH与OE相交于点G(t，t)，如图2
∵AH⊥OE于点G，A(6，0)∴∠AGO=90°∴AG2+OG2=OA2
∴(6﹣t)2+(t)2+t2+(t)2=62∴解得：t1=0(舍去)，t2=∴G(，)
设直线AG解析式为y=dx+e
∴ 解得：∴直线AG：y=﹣3x+18
当y=3时，﹣3x+18=3，解得：x=5∴H(5，3)
∴HE=9﹣5=4，点H、E关于直线x=7对称
①当HE为以点M，N，H，E为顶点的平行四边形的边时，如图2
则HE∥MN，MN=HE=4
∵点N在抛物线对称轴：直线x=7上∴xM=7+4或7﹣4，即xM=11或3
当x=3时，yM=﹣×9+×9﹣=∴M(3，)或(11，)
②当HE为以点M，N，H，E为顶点的平行四边形的对角线时，如图3
则HE、MN互相平分
∵直线x=7平分HE，点F在直线x=7上
∴点M在直线x=7上，即M为抛物线顶点
∴yM=﹣×49+×7﹣=4∴M(7，4)
综上所述，点M坐标为(3，)、(11，)或(7，4)．
重量(千克)
费用(元)
0.5
1
3
4
...
甲公司
22
67
...
乙公式
11
51
...