2017-2018学年安徽省淮南市七年级（下）期末数学试卷

这是一份2017-2018学年安徽省淮南市七年级（下）期末数学试卷，共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）下列实数中，有理数是（ ）
A．B．0.1010010001
C．D．
2．（3分）下列调查适合抽样调查的是（ ）
A．审核书稿中的错别字
B．对某社区的卫生死角进行调查
C．对八名同学的身高情况进行调查
D．对中学生目前的睡眠情况进行调查
3．（3分）如图所示，能判定直线AB∥CD的条件是（ ）
A．∠1＝∠2B．∠3＝∠4C．∠1+∠4＝180°D．∠3+∠4＝90°
4．（3分）如图，将北京市地铁部分线路图置于正方形网格中，若设定崇文门站的坐标为（0，﹣1），雍和宫站的坐标为（0，4），则西单站的坐标为（ ）
A．（0，5）B．（5，0）C．（0，﹣5）D．（﹣5，0）
5．（3分）若m＞n，下列不等式不一定成立的是（ ）
A．m+2＞n+2B．2m＞2nC．＞D．m2＞n2
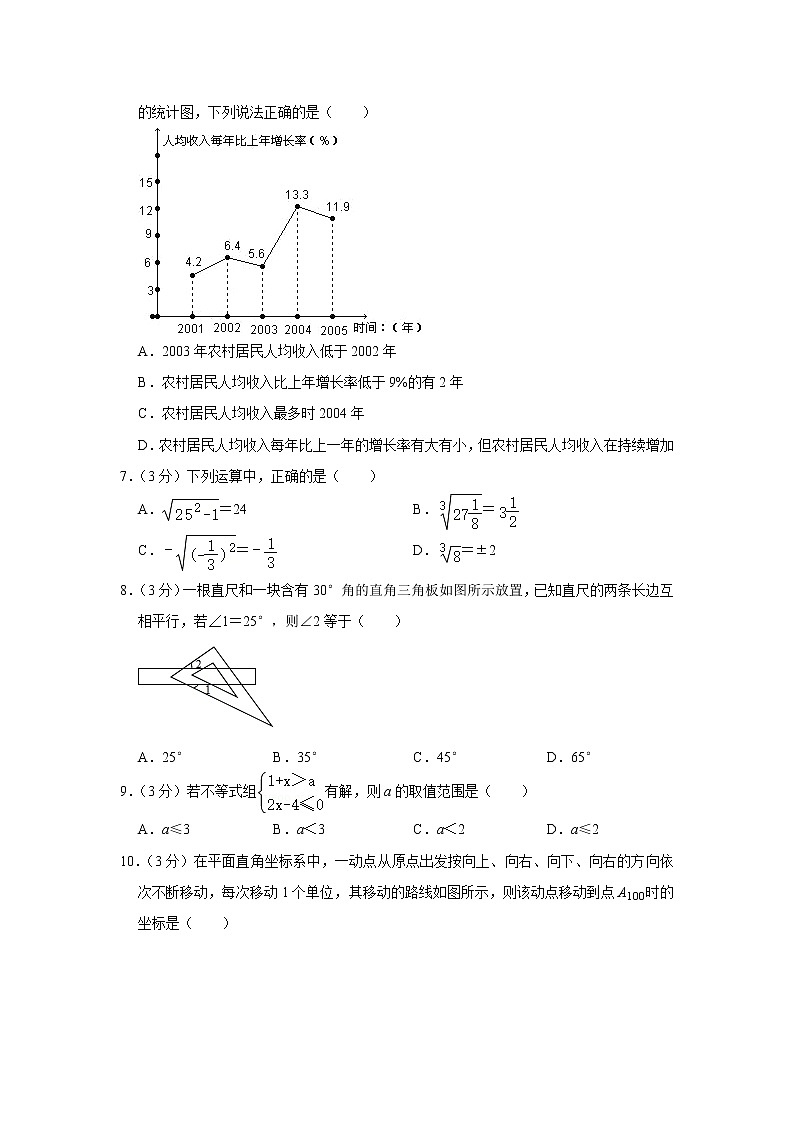
6．（3分）观察市统计局公布的“十五”时期重庆市农村居民人均收入每年比上一年增长率的统计图，下列说法正确的是（ ）
A．2003年农村居民人均收入低于2002年
B．农村居民人均收入比上年增长率低于9%的有2年
C．农村居民人均收入最多时2004年
D．农村居民人均收入每年比上一年的增长率有大有小，但农村居民人均收入在持续增加
7．（3分）下列运算中，正确的是（ ）
A．＝24B．＝
C．﹣＝﹣D．＝±2
8．（3分）一根直尺和一块含有30°角的直角三角板如图所示放置，已知直尺的两条长边互相平行，若∠1＝25°，则∠2等于（ ）
A．25°B．35°C．45°D．65°
9．（3分）若不等式组有解，则a的取值范围是（ ）
A．a≤3B．a＜3C．a＜2D．a≤2
10．（3分）在平面直角坐标系中，一动点从原点出发按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位，其移动的路线如图所示，则该动点移动到点A100时的坐标是（ ）
A．（49，0）B．（49，1）C．（50，0）D．（50，1）
二、填空题（本小题共8小题，每小题3分，共24分）
11．（3分）4的平方根是 ．
12．（3分）用不等式表示“比x的5倍大1的数不小于4”： ．
13．（3分）已知是二元一次方程ax﹣2y＝4的一个解，则a的值是 ．
14．（3分）化简：||＝ ．
15．（3分）如图，将一个长方形条折成如图所示的形状，若已知∠1＝100°，则∠2＝ °．
16．（3分）有甲、乙两个牧童，甲对乙说：“把你的羊给我1只，我的羊数就是你的羊数的2倍”．乙回答说：“最好还是把你的羊给我1只，我们的羊数就一样了．”问：两个牧童各有多少只羊？设甲牧童有x只羊，乙牧童有y只羊，可列方程组为 ．
17．（3分）已知AB∥y轴，点A的坐标为（﹣2，3），且AB＝3，则点B的坐标为 ．
18．（3分）已知实数x，y同时满足三个条件：①3x﹣2y＝4+p；②3y﹣2x＝2﹣p；③x＞y，那么实数p的取值范围是 ．
三、解答题（本题共46分）
19．（6分）解方程组：．
20．（7分）解不等式组：并把它的解集在所给数轴上表示出来．
21．（8分）如图，在由边长为1的小正方形组成的网格图中建立平面直角坐标系．
（1）直接写出点D的坐标（ ， ）；
（2）平移△ABC，使得点A与点D重合，请在坐标系中画出平移后的三角形，记为△DB1C1（其中B、C的对应点分别是B1、C1）；
（3）若P1（a，b）在线段DB1上，则其平移前的对应点P的坐标为（ ， ）．
22．（6分）完成下面填空．
已知：如图，AE平分∠BAD，AB∥CD，CD与AE相交于点F，∠CFE＝∠E，求证：AD∥BC
证明：∵AB∥CD（已知）
∴∠1＝∠ （两直线平行，同位角相等）
∵AE平分∠BAD（已知）
∴∠1＝∠ （角平分线定义）
又∵∠CFE＝∠E（已知）
∴∠ ＝∠E（等量代换）
∴AD∥BC（ ）
23．（9分）今年央视举办的“经典咏流传”节目受到中学生的广泛关注，某中学为了了解学生对观看“经典咏流传”节目的喜爱程度，对该校部分学生进行了随机抽样调查，并绘制了如下所示的两幅统计图．在条形统计图中，从左往右依次为A类（非常喜欢），B类（较喜欢），C类（一般），D类（不喜欢），已知A类和B类所占人数比是5：9，请结合两幅统计图，回答下列问题：
（1）此次抽样调查的样本容量是： ．
（2）请补全两幅统计图：并计算扇形统计图“D类（不喜欢）”部分的圆心角度数；
（3）该校有2000名学生，请你估计对观看“经典咏流传”节目较喜欢的学生人数．
24．（10分）某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克，大樱桃的进价比小樱桃的进价每千克多20元．大樱桃售价为每千克40元，小樱桃售价为每千克16元．
（1）大樱桃和小樱桃的进价分别是每千克多少元？销售完后，该水果商共赚了多少元钱？
（2）该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克，进价不变，但在运输过程中小樱桃损耗了20%．若小樱桃的售价不变，要想让第二次赚的钱不少于第一次所赚钱的90%，大樱桃的售价最少应为多少？
2017-2018学年安徽省淮南市七年级（下）期末数学试卷
参考答案与试题解析
一、选择题（本大题共10小题，每小题3分，共30分）
1．（3分）下列实数中，有理数是（ ）
A．B．0.1010010001
C．D．
【分析】依据实数的分类进行判断即可．
【解答】解：是开方开不尽的数，是无理数；
0.1010010001是有限小数，是有理数；
是开方开不尽的数，是无理数；
是无理数．
故选：B．
【点评】本题主要考查的是实数的概念，熟练掌握实数的定义是解题的关键．
2．（3分）下列调查适合抽样调查的是（ ）
A．审核书稿中的错别字
B．对某社区的卫生死角进行调查
C．对八名同学的身高情况进行调查
D．对中学生目前的睡眠情况进行调查
【分析】一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．
【解答】解：A、审核书稿中的错别字，必须准确，故必须普查；
B、此种情况数量不是很大，故必须普查；
C、人数不多，容易调查，适合普查；
D、中学生的人数比较多，适合采取抽样调查；
故选：D．
【点评】本题考查了全面调查与抽样调查的应用，一般由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似．
3．（3分）如图所示，能判定直线AB∥CD的条件是（ ）
A．∠1＝∠2B．∠3＝∠4C．∠1+∠4＝180°D．∠3+∠4＝90°
【分析】依据平行线的三条判定定理，进行判断．
【解答】解：A、B、∠1与∠2，∠3与∠4都不是直线AB与CD形成的同位角，所以不能判断直线AB∥CD，故错误；
C、根据对顶角相等，可得∠1＝∠5，∠4＝∠6，又∠1+∠4＝180°，∴∠5+∠6＝180°，根据同旁内角互补，两直线平行可得AB∥CD，故正确；
D、∠3+∠4＝90°，不符合平行线的判断条件，所以不能判断直线AB∥CD，故错误；
故选：C．
【点评】正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，不能遇到相等或互补关系的角就误认为具有平行关系，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．
4．（3分）如图，将北京市地铁部分线路图置于正方形网格中，若设定崇文门站的坐标为（0，﹣1），雍和宫站的坐标为（0，4），则西单站的坐标为（ ）
A．（0，5）B．（5，0）C．（0，﹣5）D．（﹣5，0）
【分析】首先利用已知点确定原点位置，进而得出答案．
【解答】解：如图所示：西单站的坐标为：（﹣5，0）．
故选：D．
【点评】此题主要考查了坐标确定位置，正确得出原点位置是解题关键．
5．（3分）若m＞n，下列不等式不一定成立的是（ ）
A．m+2＞n+2B．2m＞2nC．＞D．m2＞n2
【分析】根据不等式的性质1，可判断A；根据不等式的性质2，可判断B、C；根据不等式的性质3，可判断D．
【解答】解：A、不等式的两边都加2，不等号的方向不变，故A正确；
B、不等式的两边都乘以2，不等号的方向不变，故B正确；
C、不等式的两条边都除以2，不等号的方向不变，故C正确；
D、当0＞m＞n时，不等式的两边都乘以负数，不等号的方向改变，故D错误；
故选：D．
【点评】本题考查了不等式的性质，“0”是很特殊的一个数，因此，解答不等式的问题时，应密切关注“0”存在与否，以防掉进“0”的陷阱．不等式的基本性质：不等式两边加（或减）同一个数（或式子），不等号的方向不变；不等式两边乘（或除以）同一个正数，不等号的方向不变；不等式两边乘（或除以）同一个负数，不等号的方向改变
6．（3分）观察市统计局公布的“十五”时期重庆市农村居民人均收入每年比上一年增长率的统计图，下列说法正确的是（ ）
A．2003年农村居民人均收入低于2002年
B．农村居民人均收入比上年增长率低于9%的有2年
C．农村居民人均收入最多时2004年
D．农村居民人均收入每年比上一年的增长率有大有小，但农村居民人均收入在持续增加
【分析】解决本题需要从统计图获取信息，由此关键是明确图表中数据的来源及所表示的意义，对选项一一分析，选择正确答案．
【解答】解：A、2003年农村居民人均收入每年比上一年增长率低于2002年，但是，人均收入仍是增长，所以A错误；
B、农村居民人均收入比上年增长率低于9%的有3年，所以B错误；
C、农村居民人均收入比上年增长率最多时2004年，所以C错误；
D、农村居民人均收入每年比上一年的增长率有大有小，但都在增长，故D正确．
故选：D．
【点评】本题考查的是折线统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据．注意读图获取信息、分析问题解决问题的能力．
7．（3分）下列运算中，正确的是（ ）
A．＝24B．＝
C．﹣＝﹣D．＝±2
【分析】依据算术平方根的性质、立方根的性质求解即可．
【解答】解：＝＝4，故A错误；
＝，3＝＝，故B错误；
﹣＝﹣，故C正确；
＝2，故D错误．
故选：C．
【点评】本题主要考查的是立方根、平方根、算术平方根的概念，熟练掌握相关概念是解题的关键．
8．（3分）一根直尺和一块含有30°角的直角三角板如图所示放置，已知直尺的两条长边互相平行，若∠1＝25°，则∠2等于（ ）
A．25°B．35°C．45°D．65°
【分析】根据平行线性质得出∠1＝∠NFE＝25°，∠2＝∠NFG，求出∠EFG，即可求出答案．
【解答】解：
过F作FN∥AD，∵BC∥AD，
∴BC∥AD∥FN，
∴∠1＝∠NFE＝35°，∠2＝∠NFG，
∵∠G＝90°，∠E＝30°，
∴∠EFG＝60°，
∴∠2＝60°﹣25°＝35°，
故选：B．
【点评】本题考查了平行线性质，三角形内角和定理的应用，关键是根据平行线性质得出∠1＝∠NFE＝25°，∠2＝∠NFG．
9．（3分）若不等式组有解，则a的取值范围是（ ）
A．a≤3B．a＜3C．a＜2D．a≤2
【分析】先求出不等式的解集，再根据不等式组有解即可得到关于a的不等式，求出a的取值范围即可．
【解答】解：，
由①得，x＞a﹣1；
由②得，x≤2，
∵此不等式组有解，
∴a﹣1＜2，
解得a＜3．
故选：B．
【点评】本题考查的是解一元一次不等式组，熟知同大取大；同小取小；大小小大中间找；大大小小找不到的原则是解答此题的关键．
10．（3分）在平面直角坐标系中，一动点从原点出发按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位，其移动的路线如图所示，则该动点移动到点A100时的坐标是（ ）
A．（49，0）B．（49，1）C．（50，0）D．（50，1）
【分析】根据点A1、A2、A3、A4、A5、A6、A7、A8、…的坐标的变化，可找出A4n（2n，0）（n为正整数），再结合100＝4×25，即可得出A100的坐标．
【解答】解：∵A1（0，1），A2（1，1），A3（1，0），A4（2，0），A5（2，1），A6（3，1），A7（3，0），A8（4，0），…，
∴A4n（2n，0）（n为正整数）．
∵100＝4×25，
∴A100的坐标为（50，0）．
故选：C．
【点评】本题考查了规律型中点的坐标，根据点的坐标的变化找出变化规律“A4n（2n，0）（n为正整数）”是解题的关键．
二、填空题（本小题共8小题，每小题3分，共24分）
11．（3分）4的平方根是 ±2 ．
【分析】根据平方根的定义，求非负数a的平方根，也就是求一个数x，使得x2＝a，则x就是a的平方根，由此即可解决问题．
【解答】解：∵（±2）2＝4，
∴4的平方根是±2．
故答案为：±2．
【点评】本题考查了平方根的定义．注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．
12．（3分）用不等式表示“比x的5倍大1的数不小于4”： 5x+1≥4 ．
【分析】理解：不小于4就是大于等于4．
【解答】解：由题意可知5x+1≥4．
故答案是：5x+1≥4．
【点评】考查了由实际问题抽象出一元一次不等式．要抓住关键词语，弄清不等关系，把文字语言的不等关系转化为用数学符号表示的不等式．
13．（3分）已知是二元一次方程ax﹣2y＝4的一个解，则a的值是 4 ．
【分析】将x与y的值代入方程即可求出a的值．
【解答】解：将x＝2，y＝2代入方程得：2a﹣4＝4，
解得：a＝4．
故答案为：4
【点评】此题考查了二元一次方程的解，方程的解即为能使方程左右两边相等的未知数的值．
14．（3分）化简：||＝ ．
【分析】要先判断出＜0，再根据绝对值的定义即可求解．
【解答】解：∵＜0
∴||＝2﹣．
故答案为：2﹣．
【点评】此题主要考查了绝对值的性质．要注意负数的绝对值是它的相反数．
15．（3分）如图，将一个长方形条折成如图所示的形状，若已知∠1＝100°，则∠2＝ 50 °．
【分析】根据平行线的性质，即可得到∠3的度数，再根据平角的定义以及折叠的性质，即可得到∠2的度数．
【解答】解：根据长方形的对边平行，可得
∠1+∠3＝180°，
∵∠1＝100°，
∴∠3＝80°，
由折叠可得，∠2＝∠4＝（180°﹣80°）＝50°，
故答案为：50
【点评】本题主要考查了平行线的性质以及折叠的性质，解题时注意：两直线平行，同旁内角互补．
16．（3分）有甲、乙两个牧童，甲对乙说：“把你的羊给我1只，我的羊数就是你的羊数的2倍”．乙回答说：“最好还是把你的羊给我1只，我们的羊数就一样了．”问：两个牧童各有多少只羊？设甲牧童有x只羊，乙牧童有y只羊，可列方程组为 ．
【分析】设甲牧童有x只羊，乙牧童有y只羊，根据题意列出方程组解答即可．
【解答】解：设甲牧童有x只羊，乙牧童有y只羊，可得：，
故答案为：，
【点评】此题考查二元一次方程组的应用，解答此题的关键是弄清题意，设出未知数，再根据数量关系列出方程组解决问题．
17．（3分）已知AB∥y轴，点A的坐标为（﹣2，3），且AB＝3，则点B的坐标为 （﹣2，6）或（﹣2，0） ．
【分析】根据平行于y轴的点的横坐标相同可得点B的横坐标，再分点B在点A的上方与下方两种情况讨论求解．
【解答】解：∵AB∥y轴，点A的坐标为（﹣2，3），
∴点B的横坐标为﹣2，
∵AB＝3，
∴点B在点A的上方时，点B的纵坐标为6，点B的坐标为（﹣2，6），
点B在点A的下方时，点B的纵坐标为0，点B的坐标为（﹣2，0），
综上所述，点B的坐标为（﹣2，6）或（﹣2，0）
故答案为：（﹣2，6）或（﹣2，0）
【点评】本题考查了坐标与图形性质，主要利用了平行于y轴的点的横坐标相同的性质，要注意分情况讨论，作出图形更形象直观．
18．（3分）已知实数x，y同时满足三个条件：①3x﹣2y＝4+p；②3y﹣2x＝2﹣p；③x＞y，那么实数p的取值范围是 p＞﹣1 ．
【分析】首先根据：①3x﹣2y＝4+p，②3y﹣2x＝2﹣p，用p表示出x、y；然后根据x＞y，求出实数p的取值范围是多少即可．
【解答】解：①×2+②×3，可得：
5y＝14﹣p，
解得y＝2.8﹣0.2p③，
把③代入①，解得x＝3.2+0.2p，
∵x＞y，
∴3.2+0.2p＞2.8﹣0.2p，
解得p＞﹣1．
故答案为：p＞﹣1．
【点评】此题主要考查了不等式的基本性质：（1）不等式的两边同时乘以（或除以）同一个正数，不等号的方向不变；（2）不等式的两边同时乘以（或除以）同一个负数，不等号的方向改变；（3）不等式的两边同时加上（或减去）同一个数或同一个含有字母的式子，不等号的方向不变．
三、解答题（本题共46分）
19．（6分）解方程组：．
【分析】利用加减消元法求解可得．
【解答】解：①+②×5，得：44y＝660，
解得：y＝15，
将y＝15代入①，得：5x﹣15＝110，
解得：x＝25，
所以方程组的解为．
【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
20．（7分）解不等式组：并把它的解集在所给数轴上表示出来．
【分析】分别求出各不等式的解集，再求出其公共解集，并在数轴上表示出来即可．
【解答】解：解不等式①，得：x≥1，
解不等式②，得：x＜4，
所以不等式组的解集为1≤x＜4，
将解集表示在数轴上如下：
【点评】本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的法则是解答此题的关键．
21．（8分）如图，在由边长为1的小正方形组成的网格图中建立平面直角坐标系．
（1）直接写出点D的坐标（ ﹣2 ， 3 ）；
（2）平移△ABC，使得点A与点D重合，请在坐标系中画出平移后的三角形，记为△DB1C1（其中B、C的对应点分别是B1、C1）；
（3）若P1（a，b）在线段DB1上，则其平移前的对应点P的坐标为（ a+3 ， b﹣2 ）．
【分析】（1）直接利用平面直角坐标系得出D点坐标；
（2）利用D点平移规律得出各对应点位置进而得出答案；
（3）利用平移规律得出P点坐标．
【解答】解：（1）点D的坐标为：（﹣2，3）；
故答案为：﹣2，3；
（2）如图所示：△DB1C1即为所求；
（3）P1（a，b）在线段DB1上，则其平移前的对应点P的坐标为：（a+3，b﹣2）．
故答案为：a+3，b﹣2．
【点评】此题主要考查了平移变换，正确得出点的平移规律是解题关键．
22．（6分）完成下面填空．
已知：如图，AE平分∠BAD，AB∥CD，CD与AE相交于点F，∠CFE＝∠E，求证：AD∥BC
证明：∵AB∥CD（已知）
∴∠1＝∠ CFE （两直线平行，同位角相等）
∵AE平分∠BAD（已知）
∴∠1＝∠ 2 （角平分线定义）
又∵∠CFE＝∠E（已知）
∴∠ 2 ＝∠E（等量代换）
∴AD∥BC（ 内错角相等，两直线平行 ）
【分析】由AB与CD平行，利用两直线平行内错角相等得到一对角相等，再由AE为角平分线得到一对角相等，等量代换得到一对内错角相等，利用内错角相等两直线平行即可得证．
【解答】证明：∵AB∥DC（已知），
∴∠1＝∠CFE（两直线平行，同位角相等）．
∵AE平分∠BAD（已知），
∴∠1＝∠2（角平分线的定义），
∴∠CFE＝∠2（等量代换）．
∵∠CFE＝∠E（已知），
∴∠2＝∠E（等量代换），
∴AD∥BC（内错角相等，两直线平行）．
故答案为：∠CFE；∠2；∠2；内错角相等，两直线平行．
【点评】此题考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解本题的关键．
23．（9分）今年央视举办的“经典咏流传”节目受到中学生的广泛关注，某中学为了了解学生对观看“经典咏流传”节目的喜爱程度，对该校部分学生进行了随机抽样调查，并绘制了如下所示的两幅统计图．在条形统计图中，从左往右依次为A类（非常喜欢），B类（较喜欢），C类（一般），D类（不喜欢），已知A类和B类所占人数比是5：9，请结合两幅统计图，回答下列问题：
（1）此次抽样调查的样本容量是： 100 ．
（2）请补全两幅统计图：并计算扇形统计图“D类（不喜欢）”部分的圆心角度数；
（3）该校有2000名学生，请你估计对观看“经典咏流传”节目较喜欢的学生人数．
【分析】（1）根据统计图中的数据可以求得此次抽样调查的样本容量；
（2）根据统计图中的数据可以求得选择C和D的人数，B和D所占的百分比从而可以将统计图补充完整，并求得扇形统计图“D类（不喜欢）”部分的圆心角度数；
（3）根据统计图的数据可以求得对观看“经典咏流传”节目较喜欢的学生有多少人．
【解答】解：（1）此次抽样调查的样本容量是：20÷20%＝100，
故答案为：100；
（2）选择C的有：100×19%＝19人，
选择D的有：100﹣20﹣36﹣19＝25人，
B所占的百分比是：36÷100×100%＝36%，
D所占的百分比是：25÷100×100%＝25%，
补全的统计图如右图所示，
扇形统计图“D类（不喜欢）”部分的圆心角度数是：360°×25%＝90°；
（4）2000×36%＝720（人），
答：对观看“经典咏流传”节目较喜欢的学生有720人．
【点评】本题考查条形统计图、扇形统计图、用样本估计总体、样本容量，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．
24．（10分）某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克，大樱桃的进价比小樱桃的进价每千克多20元．大樱桃售价为每千克40元，小樱桃售价为每千克16元．
（1）大樱桃和小樱桃的进价分别是每千克多少元？销售完后，该水果商共赚了多少元钱？
（2）该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克，进价不变，但在运输过程中小樱桃损耗了20%．若小樱桃的售价不变，要想让第二次赚的钱不少于第一次所赚钱的90%，大樱桃的售价最少应为多少？
【分析】（1）根据用8000元购进了大樱桃和小樱桃各200千克，以及大樱桃的进价比小樱桃的进价每千克多20元，分别得出等式求出答案；
（2）根据要想让第二次赚的钱不少于第一次所赚钱的90%，得出不等式求出答案．
【解答】解：（1）设小樱桃的进价为每千克x元，大樱桃的进价为每千克y元，根据题意可得：
，
解得：，
小樱桃的进价为每千克10元，大樱桃的进价为每千克30元，
200×[（40﹣30）+（16﹣10）]＝3200（元），
∴销售完后，该水果商共赚了3200元；
（2）设大樱桃的售价为a元/千克，
（1﹣20%）×200×16+200a﹣8000≥3200×90%，
解得：a≥41.6，
答：大樱桃的售价最少应为41.6元/千克．
【点评】此题主要考查了二元一次方程组的应用以及一元一次不等式的应用，正确表示出总费用是解题关键．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2021/5/27 15:37:22；用户：独角戏；邮箱：rFmNtx6h-_TK3QDacRg2UJR_YWI@；学号：38811713