



数学九年级上册25.3 用频率估计概率优秀课件ppt
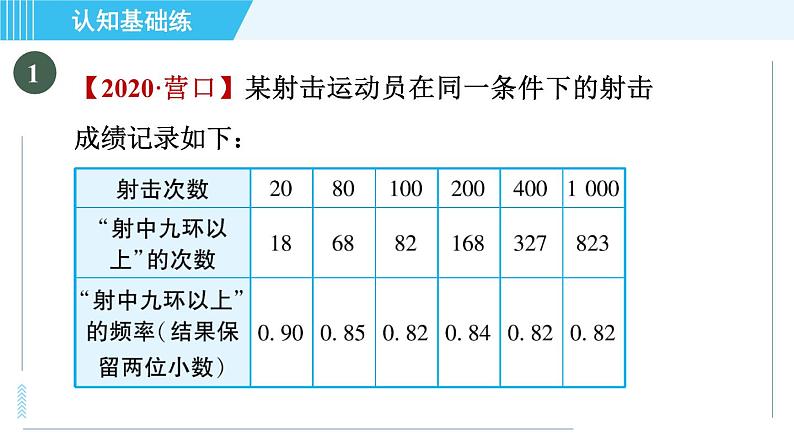
展开【2020·营口】某射击运动员在同一条件下的射击成绩记录如下:
根据频率的稳定性,估计这名运动员射击1次时“射中九环以上”的概率约是( )A.0.90 B.0.82C.0.85 D.0.84
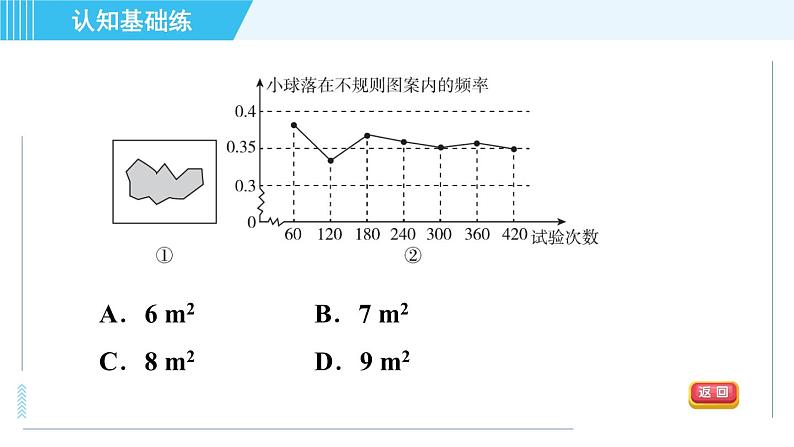
【2020·邵阳】如图①所示,平整的地面上有一个不规则的图案(图中阴影部分),小明想了解该图案的面积是多少,他采用了以下办法:用一个长为5 m,宽为4 m的长方形,将不规则图案围起来,然后在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或长方形区域外不计试验结果),他将若干次有效试验的结果绘制成了如图②所示的折线统计图,由此他估计不规则图案的面积大约为( )
A.6 m2 B.7 m2C.8 m2 D.9 m2
【2020·徐州】在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数最有可能是( )A.5 B.10C.12 D.15
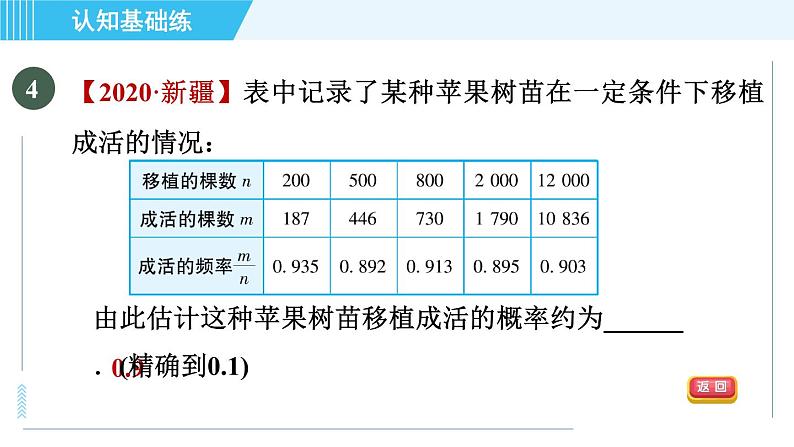
【2020·新疆】表中记录了某种苹果树苗在一定条件下移植成活的情况:
由此估计这种苹果树苗移植成活的概率约为______.(精确到0.1)
【2020·呼和浩特】公司以3元/kg的成本价购进10 000 kg柑橘,并希望出售这些柑橘能够获得12 000元利润,在出售柑橘(去掉损坏的柑橘)时,需要先进行“柑橘损坏率”统计,再大约确定每千克柑橘的售价,下面是销售部通过随机取样,得到的“柑橘损坏率”统计表的一部分,由此可估计柑橘完好的概率为________(精确到0.1);从而可大约估计每千克柑橘的实际售价为________元时(精确到0.1),可获得12 000元利润.
下列说法合理的是( )A.小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是30%B.掷一枚普通的正六面体骰子,出现6点朝上的概率 是的意思是每掷6次就有1次掷得6点朝上C.某彩票的中奖机会是2%,那么买100张彩票一定会有2张中奖D.在一次课堂进行的试验中,甲、乙两组同学估计硬币落地后,正面朝上的概率分别为0.48和0.51
错解:A诊断:用频率估计概率时,要注意试验的次数越多,事件发生的频率就会越接近这个事件发生的概率,试验的次数太少易受偶然性因素影响,此时的频率不能用来估计概率.
【2020·泰州】一个不透明袋子中装有1个白球和若干个红球,这些球除颜色外都相同.某课外学习小组做摸球试验:将球搅匀后从中任意摸出1个球,记下颜色后放回、搅匀,不断重复这个过程,获得数据如下:
(1)该学习小组发现,摸到白球的频率在一个常数附近摆动,这个常数是________(精确到0.01),由此估计出红球有________个;(2)现从该袋中一次摸出2个球,请用树状图或列表的方法列出所有等可能的结果,并求恰好摸到1个白球、1个红球的概率.
【2020·台州】某校开展线上教学,有“录播”和“直播”两种教学方式供学生选择其中一种.为分析该校学生线上学习情况,在接受这两种教学方式的学生中各随机抽取40人调查学习参与度,数据整理结果如下表(数据分组包含左端值,不包含右端值).
(1)你认为哪种教学方式学生的参与度更高?简要说明理由.
解:“直播”教学方式学生的参与度更高.理由:“直播”参与度在0.6及以上的人数为28人,“录播”参与度在0.6及以上的人数为20人,参与度在0.6及以上的“直播”人数多于“录播”人数,所以“直播”教学方式学生的参与度更高.
(2)从教学方式为“直播”的学生中任意抽取一名学生,估计该 学生的参与度在0.8及以上的概率是多少?
解:12÷40=0.3=30%.故估计该学生的参与度在0.8及以上的概率是30%.
(3)该校共有800名学生,选择“录播”和“直播”的人数之比为1:3,估计参与度在0.4以下的共有多少人?
九年级上册第二十五章 概率初步25.3 用频率估计概率教学课件ppt: 这是一份九年级上册第二十五章 概率初步25.3 用频率估计概率教学课件ppt,共19页。PPT课件主要包含了利用频率估计概率,用频率估计概率,大量重复试验,求非等可能性事件概率,列举法不能适应,频率稳定常数附近,统计思想,一种关系,频率与概率的关系等内容,欢迎下载使用。
初中数学第二十五章 概率初步25.3 用频率估计概率背景图课件ppt: 这是一份初中数学第二十五章 概率初步25.3 用频率估计概率背景图课件ppt,共21页。PPT课件主要包含了学习目标,复习旧知,提出问题引入新知,抛硬币试验,试验法,大量试验归纳方法,钉尖朝上,钉尖朝下,大量试验总结方法,频率与概率的关系等内容,欢迎下载使用。
2020-2021学年25.3 用频率估计概率课文课件ppt: 这是一份2020-2021学年25.3 用频率估计概率课文课件ppt,共41页。PPT课件主要包含了问题提出,古典概型,互斥关系,A+B+C,无数个,理论迁移,小结作业,抽签法,用Excel演示,知识迁移等内容,欢迎下载使用。













