沪科版九年级上册23.2解直角三角形及其应用课文内容ppt课件

这是一份沪科版九年级上册23.2解直角三角形及其应用课文内容ppt课件，共41页。PPT课件主要包含了答案显示，见习题，答案C，答案D，答案B，答案15米等内容，欢迎下载使用。
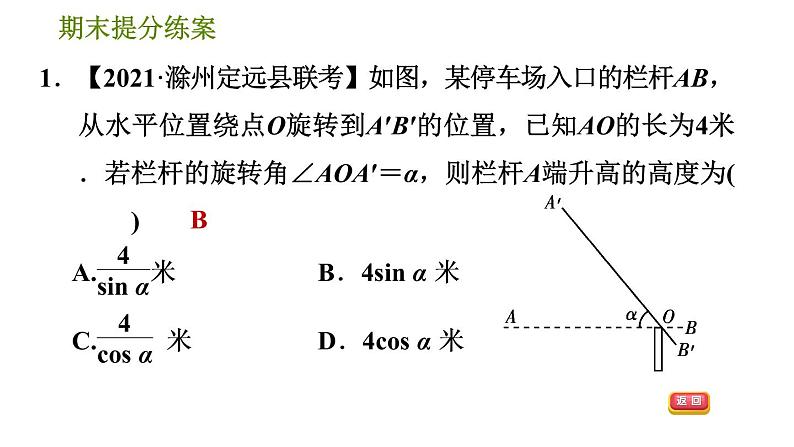
1．【2021·滁州定远县联考】如图，某停车场入口的栏杆AB，从水平位置绕点O旋转到A′B′的位置，已知AO的长为4米．若栏杆的旋转角∠AOA′＝α，则栏杆A端升高的高度为(　　)
2．【颍上期末】如图，在一笔直的海岸线l上有A，B两个观测站，船C离海岸线l的距离(即CD的长)为2 km，从A测得船C在北偏东45°的方向，从B测得船C在北偏东22.5°的方向，则AB的长为(　　)
3．【2020·合肥瑶海区校级模拟】如图，在桥外一点A测得大桥主架与水面的交汇点C的俯角为α，大桥主架的顶端D的仰角为β，已知测量点与大桥主架的水平距离AB＝a，则此时大桥主架顶端离水面的高CD为(　　)A．asinα＋asinβ B．acsα＋acsβC．atanα＋atanβ D.
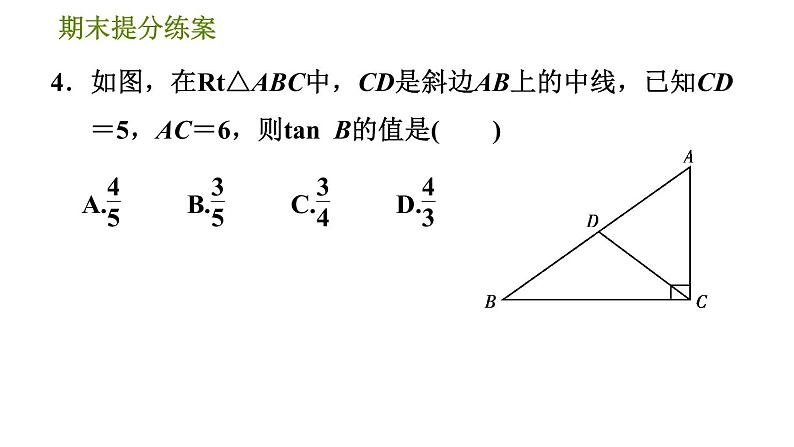
4．如图，在Rt△ABC中，CD是斜边AB上的中线，已知CD＝5，AC＝6，则tan B的值是(　　)
5．【2019·合肥庐阳区模拟】如图，在矩形ABCD中，E是BC边的中点，AE⊥BD，垂足为点F，则tan ∠AED的值是(　　)
【点拨】 ∵四边形ABCD是矩形，∴AB＝CD，∠ABC＝∠C＝90°，AD＝BC. ∵点E是BC的中点，∴BE＝CE, ∴△ABE≌△DCE，∴AE＝ED.∵AD∥BC，∴△BEF∽△DAF，
6．如图，是重庆某轻轨站入口扶梯建设示意图，起初工程师计划修建一段坡度为3∶2的扶梯AB，扶梯总长为15 m，但这样坡度太陡，扶梯太长容易引发安全事故．工程师修改方案：修建AC、DE两段扶梯，并减缓各扶梯的坡度，其中扶梯AC和平台CD形成的∠ACD为135°.从E点看D点的仰角为36.5°，AC段扶梯长18 m，则DE段扶梯长度约为(　　)
(参考数据：sin 36.5°≈ ，cs 36.5°≈ ， tan 36.5°≈ )A．43 m B．45 m C．47 m D．49 m
7．【桐城期末】一个小球沿着坡度为1∶2的坡面向下滚动了10米，此时小球下降的垂直高度为________米．
8．如图，在Rt△ABC中，∠ACB＝90°，D是AB的中点，过D点作AB的垂线交AC于点E，若BC＝6，sin A＝ ，则DE＝________．
9．【合肥包河区期末】如图，利用标杆BE测量楼房CD的高度，若标杆BE长为2.4米，且tan A＝ ，BC＝16.8米，则楼高是________．
10.如图，在数学活动课中，小敏为了测量校园内旗杆AB的高度．站在教学楼的C处测得旗杆底端B的俯角为45°，测得旗杆顶端A的仰角为30°.若旗杆与教学楼的水平距离CD为9 m，则旗杆AB的高度是________m．(结果保留根号)
11．【2020·济宁】如图，小明在距离地面30米的P处测得A处的俯角为15°，B处的俯角为60°，若斜坡AB的坡度为1∶ ，则斜坡AB的长是________米．
12．【2021·淮北五校联考】如图，某数学活动小组为测量一棵大树BH和教学楼CG的高(测角仪高AF＝1 m)，先在A处测得大树顶端H的仰角∠HFE为45°，此时教学楼顶端G恰好在视线FH上，再向前走10 m到达B处(AB＝10 m)，测得教学楼顶端G的仰角∠GED为60°，点A，B，C三点在同一水平线上．
解：在Rt△EFH中，∠HEF＝90°，∠HFE＝45°，∴HE＝EF＝AB＝10 m.∴BH＝ BE＋HE＝1＋10＝11 (m). ∴大树BH的高为11 m.
(1)求大树BH的高；
(2)求教学楼CG的高(结果保留根号)．
13．【2020·阜阳太和县模拟】如图，在△ABC中，AB＝AC＝5，cs A＝ .求底边BC的长．
14．如图，已知Rt△ABC中， ∠ACB＝90°，CD是斜边上的中线，过点B作BE⊥CD，BE分别与CD、AC相交于点F、E，FB＝2CF.(1)求sin A的值；
解：∵∠ACB＝90°，CD是斜边上的中线，∴CD＝AD，∴∠A＝∠ACD.∵∠ACB＝90°，BE⊥CD ，∴∠ACD＋∠FCB＝90°，∠ACD＋∠FEC＝90°，∴∠FEC＝∠FCB.又∵∠EFC＝∠CFB＝90°，∴△EFC∽△CFB，
(2)如果CD＝5，求AE的长．
15.【2021·桐城期末】在与水平面夹角是30°的斜坡的顶部，有一座竖直的古塔，如图是平面图，斜坡的顶部CD是水平的，在阳光的照射下，古塔AB在斜坡上的影长DE为18米，斜坡顶部的影长DB为6米，光线AE与斜坡的夹角为30°，求古塔的高．(参考数据： ≈1.4， ≈1.7)
16．【2019·合肥六区联考】现有一个“Z”型的工件(工件厚度忽略不计)，如图所示，其中AB为20 cm，BC为60 cm，∠ABC＝90°，∠BCD＝60° ，求该工件如图摆放时的高度(即A到CD的距离)．(结果精确到0.1 cm，参考数据： ≈1.73)
解：如图，过点A作AP⊥CD于点P，交BC于点Q，∵∠CQP＝∠AQB，∠CPQ＝∠B＝90°，∴∠A＝∠C＝60°.
17．【2019·成都模拟】数学活动课上，老师和学生一起去测量学校升旗台上旗杆AB的高度．如图，老师测得升旗台前斜坡FC的坡比为i＝1∶10(即EF∶CE＝1∶10)，学生小明站在离升旗台水平距离为35 m(即CE＝35 m)处的C点，测得旗杆顶端B的仰角为α，已知tan α＝，升旗台高AF＝1 m，小明身高CD＝1.6 m，请帮小明计算出旗杆AB的高度．
18．【2019·攀枝花模拟】如图，港口B位于港口A的南偏西45°方向，灯塔C恰好在AB的中点处．一艘海轮位于港口A的正南方向，港口B的南偏东45°方向的D处，它沿正北方向航行18.5 km到达E处，此时测得灯塔C在E的南偏西70°方向上，求E处距离港口A有多远．(结果精确到0.1 km，参考数据：sin 70°≈0.94，cs 70°≈0.34，tan 70°≈2.75)