





沪科版九年级上册第23章 解直角三角形23.2解直角三角形及其应用多媒体教学课件ppt
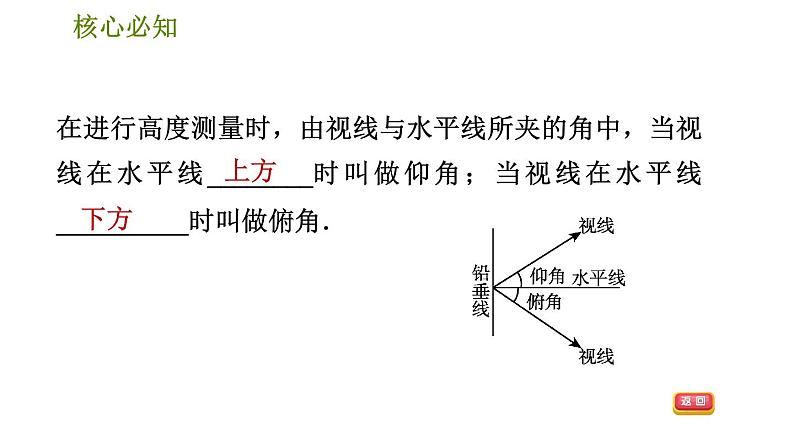
展开在进行高度测量时,由视线与水平线所夹的角中,当视线在水平线________时叫做仰角;当视线在水平线__________时叫做俯角.
1.如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
【点拨】在Rt△ABO中,∵BO=30米,∠ABO=α,∴AO=BOtan α=30tan α米.故选C.
A. 米 B.30sin α米C.30tan α米 D.30cs α米
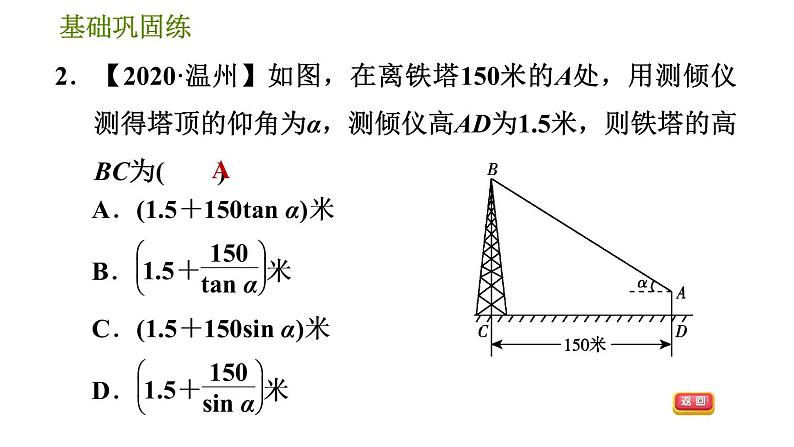
2.【2020·温州】如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为α,测倾仪高AD为1.5米,则铁塔的高BC为( )
3.【2019·孝感】如图,在P处利用测角仪测得某建筑物AB的顶端B点的仰角为60°,点C的仰角为45°,点P到建筑物的距离PD=20米,则BC=___________米.
4.【2020·亳州谯城区模拟】如图,一架飞机在点A处测得水平地面上一个标志物P的俯角为α,水平飞行m千米后到达点B处,又测得标志物P的俯角为β,那么此时飞机离地面的高度为( )
5.【2020·阜阳太和县模拟】如图,某兴趣小组用无人机进行航拍测高,无人机从1号楼和2号楼的地面正中间B点垂直起飞到高度为50米的A处,测得1号楼顶部E的俯角为60°,测得2号楼顶部F的俯角为45°.已知1号楼的高度为20米,则2号楼的高度为________米.(结果保留根号)
【点拨】如图,过点E作EG⊥AB于G,过点F作FH⊥AB于H,则四边形ECBG、四边形HBDF是矩形,∴EC=GB=20米,HB=FD.∵B为CD的中点,∴EG=CB=BD=HF.由题意得∠EAG=90°-60°=30°,∠AFH=45°.
6.【2019·合肥50中模拟】如图,为了开发利用海洋资源,某勘测飞机预测量一岛屿两端A、B的距离,飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,求岛屿两端A、B的距离.(结果精确到0.1米,参考数据: ≈1.73, ≈1.41)
解:如图,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,∵AB∥CD,∴∠AEF=∠EFB=∠ABF=90°,∴四边形ABFE为矩形,∴AB=EF,AE=BF.由题意可知AE=BF=100米,CD=500米.在Rt△AEC中, ∠C=60°,AE=100米,
7.【2019·南宁】小菁同学在数学实践活动课中测量路灯的高度.如图,已知她的目高AB为1.5米,她先站在A处看路灯顶端O的仰角为35°,再往前走3米站在C处,看路灯顶端O的仰角为65°,则路灯顶端O到地面的距离约为(已知sin 35°≈0.6,cs 35°≈0.8,tan 35°≈0.7,sin 65°≈0.9,cs 65°≈0.4,tan 65°≈2.1)( )A.3.2米 B.3.9米 C.4.7米 D.5.4米
8.【中考·安徽】如图,游客在点A处坐缆车出发,沿A-B-D的路线可至山顶D处,假设AB和BD都是直线段,且AB =BD=600 m,α=75°,β=45°,求DE的长.(参考数据:sin 75°≈0.97,cs 75°≈0.26, ≈1.41)
9.【中考·安徽】为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置一个平面镜E,使得B,E,D在同一水平线上,如图.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED),在F处测得旗杆顶A的仰角为39.3°,平面镜E的俯角为45°,FD=1.8米,问旗杆AB的高度约为多少米?(结果保留整数,参考数据:tan 39.3°≈0.82,tan 84.3°≈10.02)
10.【2019·陕西】小明想利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学们带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是,他们先在古树周围的空地上选择一点D,并在点D处安装了测倾器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,
使DG=5米,并在点G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动到点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高CD=0.5米.已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,求这棵古树的高AB.(小平面镜的大小忽略不计)
解:如图,过点C作CH⊥AB于点H,则CH=BD,BH=CD=0.5米.在Rt△ACH中, ∠ACH=45°,∴AH=CH=BD,∴AB=AH+BH=BD+0.5米.∵EF⊥FB,AB⊥FB,∴∠EFG=∠ABG=90°.由题意,易知∠EGF=∠AGB,∴△EFG∽△ABG,
湘教版九年级上册4.4 解直接三角形的应用教学课件ppt: 这是一份湘教版九年级上册4.4 解直接三角形的应用教学课件ppt,文件包含湘教版数学九年级上册441与俯角仰角有关的实际问题pptx、第1课时与俯角仰角有关的实际问题doc等2份课件配套教学资源,其中PPT共18页, 欢迎下载使用。
湘教版九年级上册4.4 解直接三角形的应用一等奖课件ppt: 这是一份湘教版九年级上册4.4 解直接三角形的应用一等奖课件ppt,共16页。PPT课件主要包含了观察与思考,俯角的概念,水平线,β60°,BCDC40m,练一练,解得x400,解直角三角形的应用等内容,欢迎下载使用。
初中数学湘教版九年级上册4.4 解直接三角形的应用完美版ppt课件: 这是一份初中数学湘教版九年级上册4.4 解直接三角形的应用完美版ppt课件,共16页。PPT课件主要包含了观察与思考,俯角的概念,水平线,铅垂线,a30°,β60°,BCDC40m,练一练,解得x400,答塔高约为45米等内容,欢迎下载使用。













