沪科版九年级上册23.1 锐角的三角函数教课ppt课件

这是一份沪科版九年级上册23.1 锐角的三角函数教课ppt课件，共34页。PPT课件主要包含了答案显示，核心必知，正弦余弦正切，见习题，答案B，答案C，1BC的长等内容，欢迎下载使用。

1．在Rt△ABC中，∠C＝90°，我们把锐角A的________与________的比叫做∠A的正弦，记作sin A；把锐角A的________与________的比叫做∠A的余弦，记作cs A．若∠A，∠B，∠C的对边分别为a，b，c，则sin A＝________，cs A＝________．
2．锐角A的________、________、________都叫做锐角A的三角函数．
1．【2021·淮北五校联考】在Rt△ABC中，∠C＝90°，BC＝5，AC＝12，则sin B的值是(　　)
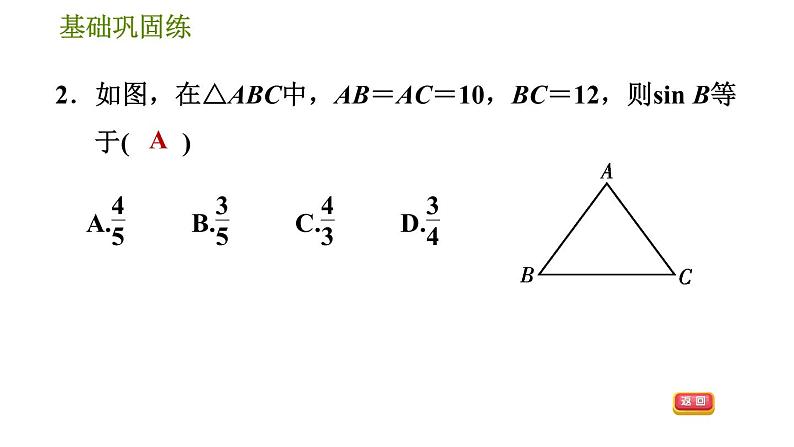
2．如图，在△ABC中，AB＝AC＝10，BC＝12，则sin B等于(　　)
3．【中考·乐山】如图，在Rt△ABC中，∠BAC＝90°，AD⊥BC于点D，则下列结论不正确的是(　　)
4．在Rt△ABC中，∠C＝90°，如果AC＝5，AB＝13，那么cs A的值为(　　)
5．【2019·桐城模拟】如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D.已知AC＝8，BC＝6，那么cs ∠ACD＝(　　)
【点拨】∵CD⊥AB于点D，∴∠BDC＝90°.∴∠B＋∠BCD＝90°.∵∠ACB＝90°，∴∠ACD＋∠BCD＝90°，∴∠ACD＝∠B.在Rt△ABC中，AC＝8，BC＝6，
6．【中考·丽水】如图，点A为∠α边上的任意一点，作AC⊥BC于点C，CD⊥AB于点D，下列用线段比表示cs α的值，错误的是(　　)
7．【2019·芜湖模拟】在△ABC中，∠C＝90°，BC＝1，AC＝2，则下列结论正确的是(　　)
8．【2020·杭州】如图，在△ABC中，∠C＝90°，设∠A，∠B，∠C所对的边分别为a，b，c，则(　　)A．c＝bsin B B．b＝csin BC．a＝btan B D．b＝ctan B
9．如图，在Rt△ABC中，CD是斜边AB上的高，AB＝c，AC＝b，BC＝a，则sin ∠BCD＝________，cs ∠ACD＝________．
10．在Rt△ABC中，∠C＝90°，已知AC＝3，BC＝6，求∠A的各个三角函数值．
11．如图，直线y＝ x＋3与x轴，y轴分别交于A，B两点，则cs ∠BAO的值是(　　)
12.【2020·聊城】如图，在4×5的正方形网格中，每个小正方形的边长都是1，△ABC的顶点都在这些小正方形的顶点上，那么sin ∠ACB的值为(　　)
13．在Rt△ABC中，∠C＝90°，tan A＝ ，则cs A的值为________，sin B的值为________．
14．【中考·宁波】如图，在菱形ABCD中，AB＝2，∠B是锐角，AE⊥BC于点E，M是AB的中点，连接MD，ME.若∠EMD＝90°，则cs B的值为________．
15．【合肥模拟】如图，点A在反比例函数y＝－ (x＜0)的图象上，点B在反比例函数y＝ (x＞0)的图象上，且∠AOB＝90°，则cs ∠OBA的值等于________．
【点拨】如图，过点A作AC⊥x轴于C，过点B作BD⊥x轴于D，易得△AOC∽△OBD，
16．【2021·桐城期末】已知：如图，在△ABC中，∠C＝90°，点D，E分别在边AB，AC上，DE∥BC，DE＝3，BC＝9.
(1)求 的值；
(2)若BD＝10，求sin A的值．
17．【2020·阜阳临泉县模拟】如图，AD是△ABC的中线， 求：
(2)∠ADC的正弦值．
18．类似在直角三角形中研究三角函数，我们新定义：等腰三角形中腰与底边的比叫做底角的邻对(can)，如图①，在△ABC中，AB＝AC，底角B的邻对记作can B，这时can B＝ 容易知道一个角的大小与这个角的邻对值是一一对应的，根据上述角的邻对的定义，解决下列问题：
(1)分别计算can 30°、can 45°和can 60°的值；