2021学年第23章 解直角三角形23.2解直角三角形及其应用教学课件ppt

这是一份2021学年第23章 解直角三角形23.2解直角三角形及其应用教学课件ppt，共25页。PPT课件主要包含了答案显示，见习题，答案B等内容，欢迎下载使用。

1．【淮南模拟】如图，滑雪场有一坡角为20°的滑雪道，滑雪道AC的长为200米，则滑雪道的坡顶到坡底的垂直高度AB的长为(　　)A．200 tan 20°米 B. 米C．200sin 20°米 D．200cs 20°米
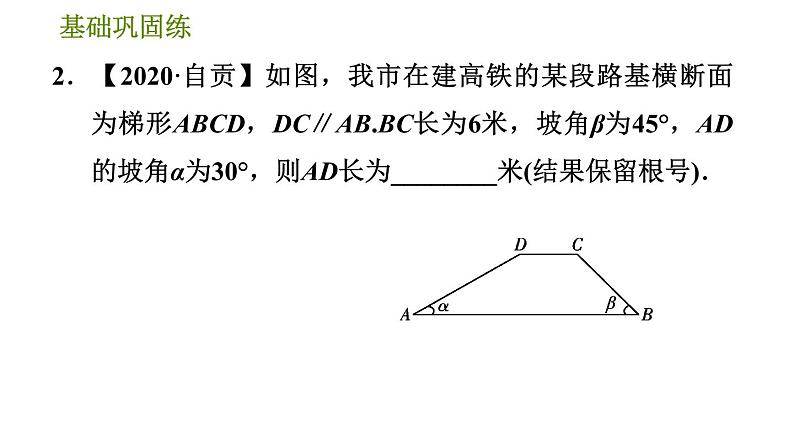
2．【2020·自贡】如图，我市在建高铁的某段路基横断面为梯形ABCD，DC∥AB.BC长为6米，坡角β为45°，AD的坡角α为30°，则AD长为________米(结果保留根号)．
3．【中考·邵阳】某商场为方便消费者购物，准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯．如图，已知原阶梯式自动扶梯AB长为10 m，坡角∠ABD为30°；改造后的斜坡式自动扶梯的坡角∠ACB为15°，请你计算改造后的斜坡式自动扶梯AC的长度．(结果精确到0.1 m，温馨提示：sin 15°≈0.26，cs 15°≈0.97，tan 15°≈0.27)
4．【2021·淮北五校联考】如图，大坝横截面的迎水坡AB的坡度i＝1∶2，即BC∶AC＝1∶2，若坡面AB的水平宽度AC为12米，则斜坡AB的长为(　　)
5．【2020·重庆】如图，在距某居民楼AB楼底B点左侧水平距离60 m的C点处有一个山坡，山坡CD的坡度(或坡比)i＝1∶0.75，山坡坡底C点到坡顶D点的距离CD＝45 m，在坡顶D点处测得居民楼楼顶A点的仰角为28°，居民楼AB与山坡CD的剖面在同一平面内，则居民楼AB的高度约为(参考数据：sin28°≈0.47，cs28°≈0.88，tan 28°≈0.53)(　　)A．76.9 m B．82.1 m C．94.8 m D．112.6 m
又CD＝45 m，即5x＝45，∴x＝9，∴EC＝3x＝27 m，DE＝FB＝4x＝36 m，∴DF＝BE＝BC＋EC＝60＋27＝87(m)，在Rt△ADF中，∠ADF＝28°，∴AF＝DF·tan 28°≈87×0.53＝46.11(m)，∴AB＝AF＋FB≈46.11＋36≈82.1(m)．故选B.
6.【2020·亳州涡阳县模拟】如图，当小明沿坡度i＝1∶ 的坡面由A到B行走了8米时，他实际上升的高度BC＝________米．
7．【2020·淮南模拟】某纪念馆示意图如图所示．某学校数学兴趣小组通过测量得知，该纪念馆外轮廓斜坡AB的坡度i＝1∶ ，底基BC＝50 m，∠ACB＝135°，求馆顶A离地面BC的距离．(结果精确到0.1 m，参考数据： ≈1.41， ≈1.73)
解：如图，过点A作AD⊥BC交BC的延长线于点D.∵∠ACB＝135°，∴∠ACD＝45°，∴△ADC为等腰直角三角形，设AD＝x m，则CD＝x m，BD＝(50＋x) m，
8.【中考·黄石】如图，为测量一座山峰CF的高度，将此山的某侧山坡划分为AB和BC两段，每一段山坡近似是“直”的，测得坡长AB＝800米，BC＝200米，坡角∠BAF＝30°，∠CBE＝45°.(1)求AB段山坡的高度EF；
(2)求山峰的高度CF( ≈ 1.414，结果精确到1米)．
9．【2020·益阳】沿江大堤经过改造后的某处横断面为如图所示的梯形ABCD，高DH＝12米，斜坡CD的坡度i＝1∶1.此处大堤的正上方有高压电线穿过，PD表示高压线上的点与堤面AD的最近距离(P，D，H在同一直线上)，在点C处测得∠DCP＝26°.(1)求斜坡CD的坡角α；
(2)电力部门要求此处高压线离堤面AD的安全距离不低于18米，请问此次改造是否符合电力部门的安全要求？(参考数据：sin 26°≈0.44，tan 26°≈0.49，sin 71°≈0.95，tan 71°≈2.90)
10．【2019·鄂州】为积极参与鄂州市全国文明城市创建活动，我市某校在教学楼顶部新建了一块大型宣传牌，如下图．小明同学为测量宣传牌的高度AB，他站在距离教学楼底部E处6米远的地面C处，测得宣传牌的底部B的仰角为60°，同时测得教学楼窗户D处的仰角为30°(A、B、D、E在同一直线上)．然后，小明沿坡度i＝1∶1.5的斜坡从C走到F处，此时DF正好与地面CE平行．
(1)求点F到直线CE的距离(结果保留根号)；
(2)若小明在F处又测得宣传牌顶部A的仰角为45°，求宣传牌的高度AB(结果精确到0.1米， ≈1.41， ≈1.73)．