数学22.3 实际问题与二次函数优质ppt课件

这是一份数学22.3 实际问题与二次函数优质ppt课件，共14页。PPT课件主要包含了几何图形最大面积问题，解题关键等内容，欢迎下载使用。

用总长为60m的篱笆围成矩形场地，矩形面积S随矩形一边长l的变化而变化.当l是多少米时，场地的面积S最大？
思考1 矩形面积公式是什么？
思考2 如何用l表示另一边？
思考3 面积S的函数关系式是什么？
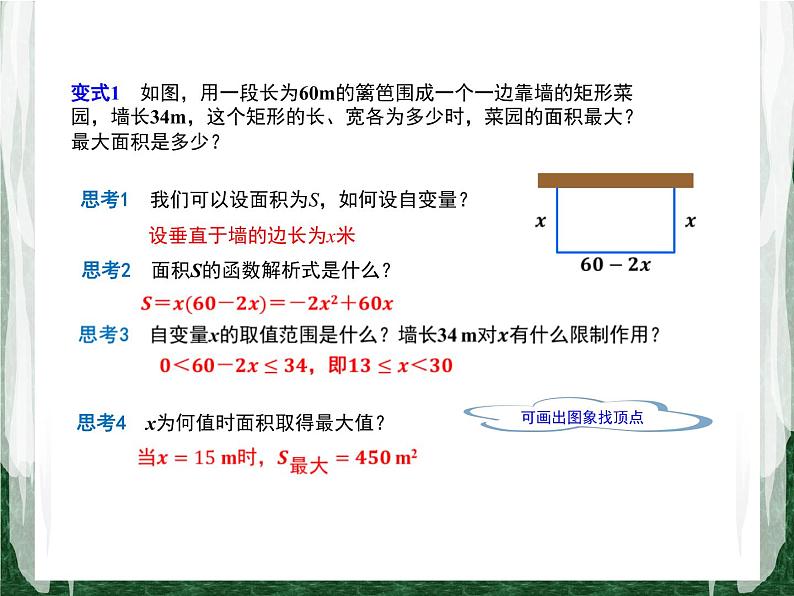
变式1 如图，用一段长为60m的篱笆围成一个一边靠墙的矩形菜园，墙长34m，这个矩形的长、宽各为多少时，菜园的面积最大？最大面积是多少？
思考1 我们可以设面积为S，如何设自变量？
设垂直于墙的边长为x米
思考2 面积S的函数解析式是什么？
思考4 x为何值时面积取得最大值？
变式2 如图，用一段长为60m的篱笆围成一个一边靠墙的矩形菜园，墙长22 m，这个矩形的长、宽各为多少时，菜园的面积最大，最大面积是多少？
思考1 仿照变式1设未知数、列函数解析式.
设垂直于墙的边长为x m，则
思考2 若设与墙平行的一边为x m，则另一边如何表示？
设矩形面积为S m2,与墙平行的一边为x m，则
思考3 当x=30时，S是否取得最大值？
注意 实际问题中求解二次函数最值问题时，函数的最值要考虑自变量的取值范围：（1）当自变量的取值包含顶点时，函数的最值在函数的顶点处取得；（2）当自变量的取值不包含顶点时，函数的最值一般在端点处取得，此时要考虑函数的增减性.
依据常见几何图形的面积公式建立函数关系式
最值有时不在顶点处，此时要利用函数的增减性来确定
A. 6厘米 B. 12厘米 C. 24厘米 D. 36厘米
3. 某广告公司设计一幅周长为16 m的矩形广告牌，广告设计费用每平方米1 000元，设矩形的一边长为x(m),面积为S(m2). (1)写出S与x之间的解析式，并写出自变量x的取值范围；（2）请你设计一个方案，使获得的设计费最多，并求出这个费用.
这时设计费最多，为16×1 000=1 6000（元）.