2021年广东省深圳市中考数学模拟试卷及答案

2020-2021年中考数学模拟试题

一．选择题（共10小题，每小题3分，共30分）

1．2021的倒数是（　　）

A．2021 B．﹣2021 C． D．﹣

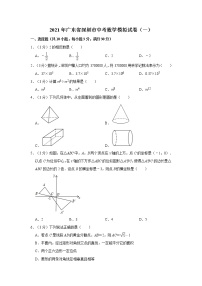
2．下列立体图形的主视图、左视图、俯视图都一样的是（　　）

        A                       B                  C                D

3．2020年6月23日，我国的北斗卫星导航系统（BDS）星座部署完成，其中一颗中高轨道卫星高度大约是21500000米．将数字21500000用科学记数法表示为（　　）

A．0.215×108 B．2.15×107 C．2.15×106 D．21.5×106

4．垃圾混置是垃圾，垃圾分类是资源．下列可回收物、有害垃圾、厨余垃圾、其他垃圾四种垃圾回收标识中，既是轴对称图形又是中心对称图形的是（　　）

            A                B                 C                D

5．下列计算正确的是（　　）

A．a2+2a2＝3a4 B．a6÷a3＝a2 

C．（a﹣b）2＝a2﹣b2 D．（ab）2＝a2b2

6．刘老师对所在班级的全体学生进行实地家访，了解到每名学生家庭的有关信息，现从中随机抽取15名学生家庭的年收入情况，数据如下表：

关于这15名学生家庭的年收入情况，下列说法不正确的是（　　）

A．平均数是4万元 B．中位数是3万元 

C．众数是3万元 D．极差是11万元

7．下列命题是假命题的是（　　）

A．三角形的外心到三角形的三个顶点的距离相等 

B．如果等腰三角形的两边长分别是5和6，那么这个等腰三角形的周长为16 

C．将一次函数y＝3x﹣1的图象向上平移3个单位，所得直线不经过第四象限 

D．若关于x的一元一次不等式组无解，则m的取值范围是m≤1

8．如图，在菱形ABCD中，按以下步骤作图：①分别以点C和点D为圆心，大于CD的同样的长为半径作弧，两弧交于M，N两点；②作直线MN，交CD于点E，连接BE．若直线MN恰好经过点A，则下列说法错误的是（　　）

A．∠ABC＝60° 

B．S△ABE＝2S△ADE 

C．若AB＝4，则BE＝4 

D．tan∠CBE＝

9．如图是抛物线y＝ax2+bx+c（a≠0）的部分图象，其顶点坐标为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间，则下列结论：

①4a﹣2b+c＞0；

②3a+b＞0；

③b2＝4a（c﹣n）；

④一元二次方程ax2+bx+c＝n﹣1有两个互异实根．

其中正确结论的个数是（　　）

A．1个 B．2个 C．3个 D．4个

10．如图，正方形ABCD中，E是BC延长线上一点，在AB上取一点F，使点B关于直线EF的对称点G落在AD上，连接EG交CD于点H，连接BH交EF于点M，连接CM．则下列结论，其中正确的是（　　）

①∠1＝∠2；

②∠3＝∠4；

③GD＝CM；

④若AG＝1，GD＝2，则BM＝．

A．①②③④ B．①② C．③④ D．①②④

二．填空题（共5小题，每小题3分，共15分）

11．在实数范围内分解因式：8x3y﹣2xy3＝　           　．

12．一个布袋内只装有1个黑球和2个白球，这些球除颜色外其余都相同，随机摸出一个球后放回搅匀，再随机摸出一个球，则两次摸出的球都是黑球的概率是　   　．

13．对于三个数a，b，c，我们规定用M{a，b，c}表示这三个数的平均数，用min{a，b，c}表示这三个数中最小的数．例如：M{﹣1，2，3}＝＝，min{﹣1，2，3}＝﹣1，如果M{3，2x+1，4x﹣1}＝min{2，﹣x+3，5x}，那么x＝　   　．

14．如图，△AOB中，∠AOB＝90°，AO＝3，BO＝6，△AOB绕顶点O逆时针旋转到△A′OB′处，此时线段A′B′与BO的交点E为BO的中点，则线段B′E的长度为　   　．

                  第14题                             第15题

15．如图，在▱ABCD中，点B在y轴上，AD过原点，且S▱ABCD＝12，A、C、D三点在反比例函数y＝（k≠0）的图象上，则k＝　   　．

三．解答题（共55小题）

16．（5分）计算：

17．（6分）先化简，再求值：，其中a＝+1．

18．（8分）为了解学生的艺术特长发展情况，某校音乐决定围绕在“舞蹈、乐器、声乐、戏曲、其他活动”项目中，你最喜欢哪一项活动（每人只限一项）的问题，在全校范围内随机抽取部分学生进行问卷调查，并将调查结果绘制如下两幅不完整的统计图．请你根据统计图解答下列问题：

（1）在这次调查中，一共抽查了　  　名学生，其中喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为　  　．扇形统计图中喜欢“戏曲”部分扇形的圆心角为　  　度．

（2）请你补全条形统计图．

（3）若在“舞蹈、乐器、声乐、戏曲”项目中任选两项成立课外兴趣小组，请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项的概率．

19．（8分）如图，△ABC中，∠BCA＝90°，CD是边AB上的中线，分别过点C，D作BA，BC的平行线交于点E，且DE交AC于点O，连接AE．

（1）求证：四边形ADCE是菱形；

（2）若AC＝2DE，求sin∠CDB的值．

20．（8分）随着人们“节能环保，绿色出行”意识的增强，越来越多的人喜欢骑自行车出行，也给自行车商家带来商机．某自行车行经营的A型自行车去年销售总额为8万元．今年该型自行车每辆售价预计比去年降低200元．若该型车的销售数量与去年相同，那么今年的销售总额将比去年减少10%，求：

（1）A型自行车去年每辆售价多少元？

（2）该车行今年计划新进一批A型车和新款B型车共60辆，且B型车的进货数量不超过A型车数量的两倍．已知A型车和B型车的进货价格分别为1500元和1800元，计划B型车销售价格为2400元，应如何组织进货才能使这批自行车销售获利最多？

21．（10分）已知Rt△ABC，∠BAC＝90°，点D是BC中点，AD＝AC，BC＝2，过A，D两点作⊙O，交AB于点E．

（1）求证：BC是⊙O的切线；

（2）如图1，当圆心O在AB上且点M是⊙O上一动点，连接DM交AB于点N，求当ON等于多少时，三点D、E、M组成的三角形是等腰三角形？

（3）如图2，当圆心O不在AB上且动圆⊙O与DB相交于点Q时，过D作DH⊥AB（垂足为H）并交⊙O于点P，问：当⊙O变动时，DP﹣DQ的值变不变？若不变，请求出其值；若变化，请说明理由．

22．（10分）如图一，已知抛物线y＝ax2+bx+c的图象经过点A（0，3）、B（1，0），其对称轴为直线l：x＝2，过点A作AC∥x轴交抛物线于点C，∠AOB的平分线交线段AC于点E，点P是抛物线上的一个动点，设其横坐标为m．

（1）求抛物线的解析式；

（2）若动点P在直线OE下方的抛物线上，连接PE、PO，当m为何值时，四边形AOPE面积最大，并求出其最大值；

（3）如图二，F是抛物线的对称轴l上的一点，在抛物线上是否存在点P，使△POF成为以点P为直角顶点的等腰直角三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由．

参考答案

一、选择题（共1小题，每小题5分，共30分）

二、填空题（共5小题，每小题3分，共15分）

11、     12、    13、或    14、    15、4

三、解答题：

16、（5分）解：原式＝4×﹣（2﹣）+1﹣2+4

＝2﹣2++1﹣2+4

＝+3

17、（6分）解：（﹣）÷

＝

＝

＝

＝，

当a＝+1时，原式＝＝．

18、（8分）解：（1）一共抽查学生数为：8÷16%＝50，

“舞蹈”活动项目的人数占抽查总人数的百分比为：×100%＝24%；

∵喜欢戏曲的人数：50﹣12﹣16﹣8﹣10＝50﹣46＝4人，

∴扇形统计图中喜欢“戏曲”部分扇形的圆心角为：×360°＝28.8°，

（2）补全统计图如图：

（3）画树状图如下：

∵共有12种等可能结果，其中恰好选中“舞蹈、声乐”这两项活动的有2种结果，

故恰好选中“舞蹈、声乐”两项活动的概率是：＝．

19、（8分）（1）证明：∵DE∥BC，CE∥AB，

∴四边形DBCE是平行四边形．

∴CE＝BD，

又∵CD是边AB上的中线，

∴BD＝AD，

∴CE＝DA，

又∵CE∥DA，

∴四边形ADCE是平行四边形．

∵∠BCA＝90°，CD是斜边AB上的中线，

∴AD＝CD，

∴四边形ADCE是菱形；

（2）解：过点C作CF⊥AB于点F，

由（1）可知，BC＝DE，

设BC＝x，则AC＝2x，

在Rt△ABC中，AB＝＝x．

∵AB•CF＝AC•BC，

∴CF＝＝x．

∵CD＝AB＝x，

∴sin∠CDB＝＝．

20、（8分）解：（1）设去年A型车每辆售价x元，则今年售价每辆为（x﹣200）元，由题意得

＝，

解得：x＝2000．

经检验，x＝2000是原方程的根．

答：去年A型车每辆售价为2000元；

（2）设今年新进A型车a辆，则B型车（60﹣a）辆，获利y元，由题意，得

y＝（2000﹣200﹣1500）a+（2400﹣1800）（60﹣a），

y＝﹣300a+36000．

∵B型车的进货数量不超过A型车数量的两倍，

∴60﹣a≤2a，

∴a≥20．

∵y＝﹣300a+36000．

∴k＝﹣300＜0，

∴y随a的增大而减小．

∴a＝20时，y有最大值，

∴B型车的数量为：60﹣20＝40（辆）．

∴当新进A型车20辆，B型车40辆时，这批车获利最大．

21、（10分）证明：（1）如图1，连接CO，

∵Rt△ABC，∠BAC＝90°，点D是BC中点，

∴AD＝CD＝BD，

∵AD＝AC，

∴AC＝CD，

又∵AO＝DO，CO＝CO，

∴△ACO≌△DCO（SSS），

∴∠CDO＝∠CAO＝90°，

又∵OD是半径，

∴BC是⊙O的切线；

（2）连DE、ME，如图3，

∵DM＞DE，

当ED和EM为等腰三角形EDM的两腰，

∴OE⊥DM，

又∵AD＝AC，

∴△ADC为等边三角形，

∴∠CAD＝60°，

∴∠DAO＝30°，

∴∠DON＝60°，

在Rt△ADN中，DN＝AD＝，

在Rt△ODN中，ON＝DN＝，

∴当ON等于时，三点D、E、M组成的三角形是等腰三角形；

当MD＝ME，DE为底边，如图4，作DH⊥AE，

∵AD＝，∠DAE＝30°，

∴DH＝，∠DEA＝60°，DE＝1，

∴△ODE为等边三角形，

∴OE＝DE＝1，OH＝，

∵∠M＝∠DAE＝30°，

而MD＝ME，

∴∠MDE＝75°，

∴∠ADM＝90°﹣75°＝15°，

∴∠DNO＝45°，

∴△NDH为等腰直角三角形，

∴NH＝DH＝，

∴ON＝﹣；

综上所述，当三点D、E、M组成的三角形是等腰三角形时，ON等于或﹣；

（3）当⊙O变动时DP﹣DQ的值不变，DP﹣DQ＝，

理由如下：连AP、AQ，如图2，

∵∠C＝∠CAD＝60°，

而DP⊥AB，

∴AC∥DP，

∴∠PDB＝∠C＝60°，

又∵∠PAQ＝∠PDB，

∴∠PAQ＝60°，

∴∠CAQ＝∠PAD，

∵AC＝AD，∠AQC＝∠P，

∴△AQC≌△APD（AAS），

∴DP＝CQ，

∴DP﹣DQ＝CQ﹣DQ＝CD＝．

22、（10分）解：（1）设抛物线与x轴的另一个交点为D，

由对称性得：D（3，0），

设抛物线的解析式为：y＝a（x﹣1）（x﹣3），

把A（0，3）代入得：3＝3a，a＝1，

∴抛物线的解析式；y＝x2﹣4x+3；

（2）如图1，

∵△AOE的面积是定值，所以当△OEP面积最大时，四边形AOPE面积最大，

设P（m，m2﹣4m+3），

∵OE平分∠AOB，∠AOB＝90°，

∴∠AOE＝45°，

∴△AOE是等腰直角三角形，

∴AE＝OA＝3，

∴E（3，3），则OE的解析式为：y＝x，

过P作PG∥y轴，交OE于点G，

∴G（m，m），

∴PG＝m﹣（m2﹣4m+3）＝﹣m2+5m﹣3，

∴S四边形AOPE＝S△AOE+S△POE＝×3×3+PG•AE＝+×3×（﹣m2+5m﹣3）＝﹣m2+，

∵﹣＜0，

∴当m＝时，S有最大值为，此时点P（，﹣）；

（3）存在，理由：

①当P在对称轴的左边，且在x轴下方时，

如图2，过P作MN⊥y轴，交y轴于M，交l于N，

∵△OPF是等腰直角三角形，且OP＝PF，

∴△OMP≌△PNF（AAS），

∴OM＝PN，

∵P（m，m2﹣4m+3），则﹣m2+4m﹣3＝2﹣m，

解得：m＝（舍去）或

∴P的坐标为（，）；

②当P在对称轴的左边，且在x轴上方时，如图3，

同理得：2﹣m＝m2﹣4m+3，解得：m＝或（舍去），

故点P（，）；

③当P在对称轴的右边，且在x轴下方时，

如图3，过P作MN⊥x轴于N，过F作FM⊥MN于M，

同理得△ONP≌△PMF，

∴PN＝FM，

则﹣m2+4m﹣3＝m﹣2，

解得：m＝或（舍去），

P的坐标为（，）；

④当P在对称轴的右边，且在x轴上方时，

同理得m2﹣4m+3＝m﹣2，

解得：m＝或（舍去），

点P的坐标为：（，）；

综上，点P的坐标为：（，）或（，）或（，）或（，）．