
考点16 反比例函数—2021年《三步冲刺中考•数学》(全国通用)之第1步小题夯基础(原卷+解析)
展开第一步 小题夯基础
考点16 反比例函数
真题回顾
1.(2020·衡阳)反比例函数 经过点 ,则下列说法错误的是( )
A. B. 函数图象分布在第一、三象限
C. 当 时, 随 的增大而增大 D. 当 时, 随 的增大而减小
2.(2020·阜新)若 与 都是反比例函数 图象上的点,则a的值是( )
A. 4 B. -4 C. 2 D. -2
3.(2020·山西)已知点 , , 都在反比例函数 的图像上,且 ,则 , , 的大小关系是( )
A. B. C. D.
4.(2020·潍坊)如图,函数 与 的图象相交于点 两点,则不等式 的解集为( )
A. B. 或 C. D. 或
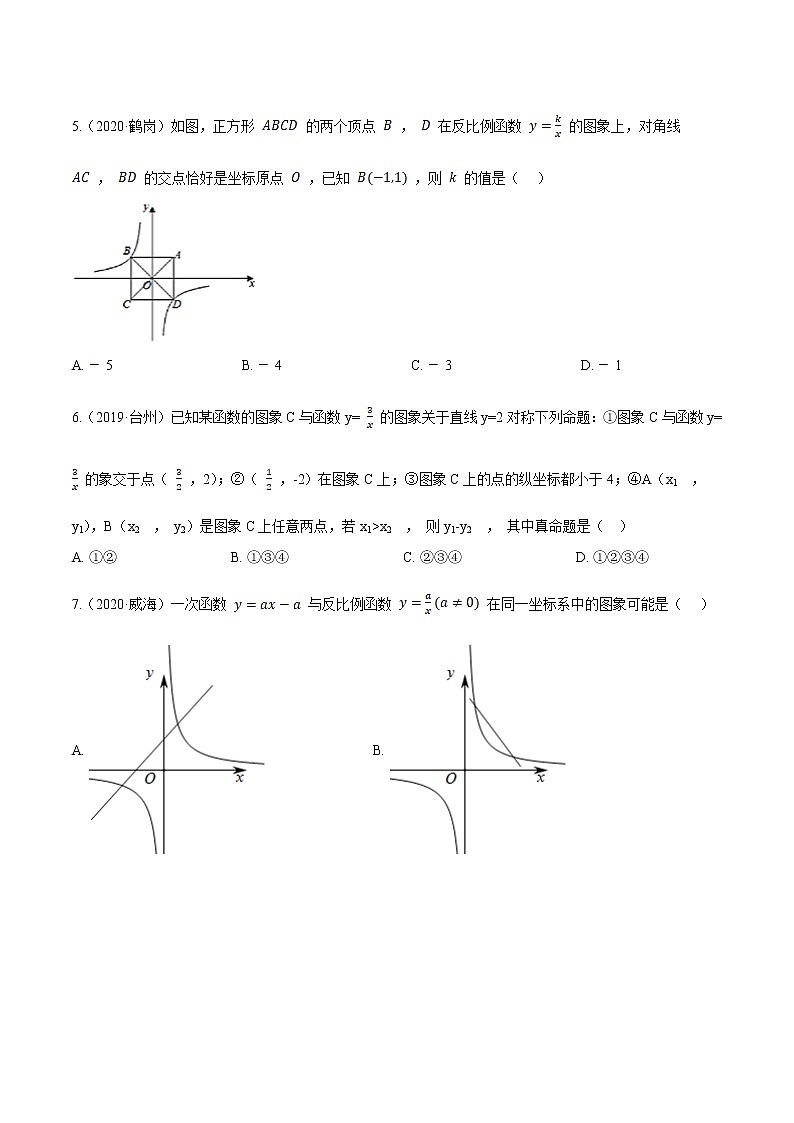
5.(2020·鹤岗)如图,正方形 的两个顶点 , 在反比例函数 的图象上,对角线 , 的交点恰好是坐标原点 ,已知 ,则 的值是( )
A. 5 B. 4 C. 3 D. 1
6.(2019·台州)已知某函数的图象C与函数y= 的图象关于直线y=2对称下列命题:①图象C与函数y= 的象交于点( ,2);②( ,-2)在图象C上;③图象C上的点的纵坐标都小于4;④A(x1 , y1),B(x2 , y2)是图象C上任意两点,若x1>x2 , 则y1-y2 , 其中真命题是( )
A. ①② B. ①③④ C. ②③④ D. ①②③④
7.(2020·威海)一次函数 与反比例函数 在同一坐标系中的图象可能是( )
A. B.
C. D.
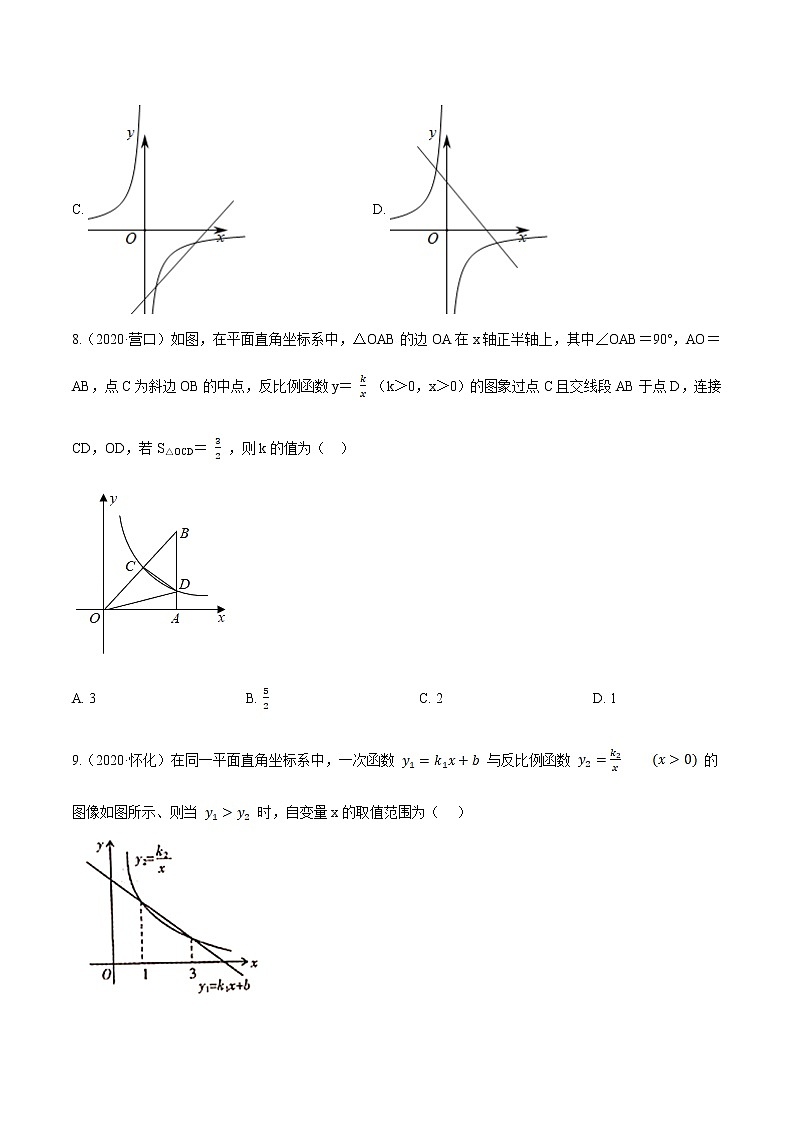
8.(2020·营口)如图,在平面直角坐标系中,△OAB的边OA在x轴正半轴上,其中∠OAB=90°,AO=AB,点C为斜边OB的中点,反比例函数y= (k>0,x>0)的图象过点C且交线段AB于点D,连接CD,OD,若S△OCD= ,则k的值为( )
A. 3 B. C. 2 D. 1
9.(2020·怀化)在同一平面直角坐标系中,一次函数 与反比例函数 的图像如图所示、则当 时,自变量x的取值范围为( )
A. B. C. D.
10.(2017·临沂)如图,在平面直角坐标系中,反比例函数y= (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
A. 6 B. 10 C. 2 D. 2
11.(2020·毕节)一次函数 的图象与反比例函数 的图象的两个交点分别是 , ,则 ________.
12.(2020·达县)如图,点A、B在反比函数 的图象上,A、B的纵坐标分别是3和6,连接 、 ,则 的面积是________.
13.(2020·沈阳)如图,在平面直角坐标系中,O是坐标原点,在 中, 于点C,点A在反比例函数 的图象上,若OB=4,AC=3,则k的值为________.
14.(2018·安顺)如图,已知直线 与x轴、y轴相交于P、Q两点,与 的图象相交于 、 两点,连接OA、OB.给出下列结论:① ;② ;③ ;④不等式 的解集是 或 .
其中正确结论的序号是________.
15.(2019·郴州)如图,点A,C分别是正比例函数 的图象与反比例函数 的图象的交点,过A点作 轴于点D,过C点作 轴于点B,则四边形ABCD的面积为________.
模拟预测
1.(2020·温州模拟)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压 与气体体积 之间的函数关系如图所示.当气球的体积是 ,气球内的气压是( ) .
A. 96 B. 150 C. 120 D. 64
2.(2020·武汉模拟)反比例函数y= 的图象上有三点(x1 , ﹣1),B(x2 , a),C(x3 , 3),当x3<x2<x1时,a的取值范围为( )
A. a>3 B. a<﹣1 C. ﹣1<a<3 D. a>3或a<﹣1
3.(2020·武汉模拟)如图直线y1=x+1与双曲线y2= 交于A (2,m)、B(﹣3,n)两点.则当y1>y2时,x的取值范围是( )
A. x>﹣3或0<x<2 B. ﹣3<x<0或x>2 C. x<﹣3或0<x<2 D. ﹣3<x<2
4.(2020·江阴模拟)如图,▱OABC的周长为7,∠AOC=60°,以O为原点,OC所在直线为x轴建立直角坐标系,函数 (x>0)的图像经过▱OABC的顶点A和BC的中点M,则k的值为( )
A. B. 12 C. D. 6
5.(2020·铜仁模拟)如图所示,已知A( ,y1),B(2,y2)为反比例函数 图像上的两点,动点P(x,0)在x正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
A. ( ,0) B. (1,0) C. ( ,0) D. ( ,0)
6.(2020·泰州模拟)若反比例函数 的图象经过第一、三象限,则 k的取值范围是________.
7.(2020·江都模拟)若双曲线 与直线 无交点,则k的取值范围是________.
8.(2020·丰台模拟)如图,正比例函数 的图象和反比例函数 的图象交于A,B两点,分别过点A,B作 轴的垂线,垂足为点C,D,则△ 与 的面积之和为________.
9.(2020·铜川模拟)如图, 的三个顶点分别为 .若反比例函数 在第一象限内的图象与 有交点,则 的取值范围是________.
10.(2020·阜宁模拟)如图,在平面直角坐标系中,反比例函数 与正比例函数 的图像分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
第一步 小题夯基础
考点16 反比例函数
真题回顾
1.(2020·衡阳)反比例函数 经过点 ,则下列说法错误的是( )
A. B. 函数图象分布在第一、三象限
C. 当 时, 随 的增大而增大 D. 当 时, 随 的增大而减小
【答案】 C
【考点】反比例函数的性质
【解析】【解答】将点(2,1)代入 中,解得:k=2,A.k=2,不符合题意;
B.k=2﹥0,反比例函数图象分布在第一、三象限,不符合题意;
C.k=2﹥0且x﹥0,函数图象位于第一象限,且y随x的增大而减小,符合题意;
D.k=2﹥0且x﹥0,函数图象位于第一象限,且y随x的增大而减小,不符合题意;
故答案为:C.
【分析】将点(2,1)代入 中求出k值,再根据反比例函数的性质对四个选项逐一分析即可.
2.(2020·阜新)若 与 都是反比例函数 图象上的点,则a的值是( )
A. 4 B. -4 C. 2 D. -2
【答案】 B
【考点】待定系数法求反比例函数解析式
【解析】【解答】解:∵点 是反比例函数 图象上的点;
∴k=2×4=8
∴反比例函数解析式为:
∵点 是反比例函数 图象上的点,
∴a=-4
故答案为:B.
【分析】先把用 代入确定反比例函数的比例系数k,然后求出函数解析式,再把点(-2,a)代入可求a的值.
3.(2020·山西)已知点 , , 都在反比例函数 的图像上,且 ,则 , , 的大小关系是( )
A. B. C. D.
【答案】 A
【考点】反比例函数的性质
【解析】【解答】解: 反比例函数 ,
反比例函数图像在第二、四象限,
观察图像:当 时,
则 .
故答案为:A.
【分析】首先画出反比例函数 ,利用函数图像的性质得到当 时, , , 的大小关系.
4.(2020·潍坊)如图,函数 与 的图象相交于点 两点,则不等式 的解集为( )
A. B. 或 C. D. 或
【答案】 D
【考点】反比例函数与一次函数的交点问题
【解析】【解答】解:∵函数 与 的图象相交于点 两点,
∴不等式 的解集为: 或 ,
故答案为:D .
【分析】结合图像,求出一次函数图象在反比例函数图象上方所对应的自变量的范围即可.
5.(2020·鹤岗)如图,正方形 的两个顶点 , 在反比例函数 的图象上,对角线 , 的交点恰好是坐标原点 ,已知 ,则 的值是( )
A. 5 B. 4 C. 3 D. 1
【答案】 D
【考点】反比例函数图象上点的坐标特征
【解析】【解答】∵点 在反比例函数 的图象上, ,
∴ ,
∴ ,
故答案为:D.
【分析】把点B代入反比例函数 即可得出答案.
6.(2019·台州)已知某函数的图象C与函数y= 的图象关于直线y=2对称下列命题:①图象C与函数y= 的象交于点( ,2);②( ,-2)在图象C上;③图象C上的点的纵坐标都小于4;④A(x1 , y1),B(x2 , y2)是图象C上任意两点,若x1>x2 , 则y1-y2 , 其中真命题是( )
A. ①② B. ①③④ C. ②③④ D. ①②③④
【答案】 A
【考点】反比例函数的性质,反比例函数图象上点的坐标特征
【解析】【解答】解:由图像C与反比例函数y= 关于y=2对称可得如下图,
①当x= 时,y=2,故①正确;
②当x= 时,y1=6,即( ,6)关于y=2时的对称点为( ,-2),故②正确;
③如图:y= 与y=2之间距离小于2,即C与x轴间距离小于4(C右侧图),但y轴左侧与x轴距离大于4,故③错误;
④当x>0时,x1>x2 , 则y1>y2;当x<0时,x1>x2 , 则y1>y2;
∵不管x>0还是x<0时,图像都是增函数,
∴x1>x2时则y1>y2;故④错误.
故答案为:A.
【分析】根据题意画出图形,①将x= 代入y= 得y=2,从而可判断①正确;
②令x= 时,y1=6,即( ,6)关于y=2时的对称点为( ,-2),从而可判断②正确;
③根据图形分析可得C右侧图与x轴间距离小于4,但y轴左侧与x轴距离大于4,从而可判断③错误;
④由图像可知不管x>0还是x<0时,图像都是增函数,从而可判断④错误.
7.(2020·威海)一次函数 与反比例函数 在同一坐标系中的图象可能是( )
A. B.
C. D.
【答案】 D
【考点】反比例函数与一次函数的交点问题
【解析】【解答】当 时, ,则一次函数 经过一、三、四象限,反比例函数 经过一 、三象限,故排除A,C选项;
当 时, ,则一次函数 经过一、二、四象限,反比例函数 经过二、四象限,故排除B选项,
故答案为:D.
【分析】根据一次函数与反比例函数图象的性质进行判断即可得解.
8.(2020·营口)如图,在平面直角坐标系中,△OAB的边OA在x轴正半轴上,其中∠OAB=90°,AO=AB,点C为斜边OB的中点,反比例函数y= (k>0,x>0)的图象过点C且交线段AB于点D,连接CD,OD,若S△OCD= ,则k的值为( )
A. 3 B. C. 2 D. 1
【答案】 C
【考点】反比例函数与一次函数的交点问题
【解析】【解答】解:根据题意设B(m,m),则A(m,0),
∵点C为斜边OB的中点,
∴C( , ),
∵反比例函数y= (k>0,x>0)的图象过点C,
∴k= = ,
∵∠OAB=90°,
∴D的横坐标为m,
∵反比例函数y= (k>0,x>0)的图象过点D,
∴D的纵坐标为 ,
作CE⊥x轴于E,
∵S△COD=S△COE+S梯形ADCE﹣S△AOD=S梯形ADCE , S△OCD= ,
∴ (AD+CE)•AE= ,即 ( )•(m﹣ m)= ,
∴ =1,
∴k= =2,
故答案为:C.
【分析】根据题意设B(m,m),则A(m,0),C( , ),D(m, m),然后根据S△COD=S△COE+S梯形ADCE﹣S△AOD=S梯形ADCE , 得到 ( )•(m﹣ m)= ,即可求得k= =2.
9.(2020·怀化)在同一平面直角坐标系中,一次函数 与反比例函数 的图像如图所示、则当 时,自变量x的取值范围为( )
A. B. C. D.
【答案】 D
【考点】反比例函数与一次函数的交点问题
【解析】【解答】解:由图像可得:两个交点的横坐标分别是:
所以:当 时,
,
故答案为:D.
【分析】观察图像得到两个交点的横坐标,再观察一次函数函数图像在反比例函数图像上方的区段,从而可得答案.
10.(2017·临沂)如图,在平面直角坐标系中,反比例函数y= (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
A. 6 B. 10 C. 2 D. 2
【答案】 C
【考点】反比例函数的性质
【解析】【解答】解:∵正方形OABC的边长是6,
∴点M的横坐标和点N的纵坐标为6,
∴M(6, ),N( ,6),
∴BN=6﹣ ,BM=6﹣ ,
∵△OMN的面积为10,
∴6×6﹣ ×6× ﹣ 6× ﹣ ×(6﹣ )2=10,
∴k=24,
∴M(6,4),N(4,6),
作M关于x轴的对称点M′,连接NM′交x轴于P,则NM′的长=PM+PN的最小值,
∵AM=AM′=4,
∴BM′=10,BN=2,
∴NM′= = =2 ,
故选C.
【分析】由正方形OABC的边长是6,得到点M的横坐标和点N的纵坐标为6,求得M(6, ),N( ,6),根据三角形的面积列方程得到M(6,4),N(4,6),作M关于x轴的对称点M′,连接NM′交x轴于P,则NM′的长=PM+PN的最小值,根据勾股定理即可得到结论.
11.(2020·毕节)一次函数 的图象与反比例函数 的图象的两个交点分别是 , ,则 ________.
【答案】 -2
【考点】反比例函数与一次函数的交点问题
【解析】【解答】解:先将点A(-1,-4)、B(2,m)代入反比例函数 中,
得:k=(-1)×(-4)=4, ,
将点A(-1,-4)、B(2,2)代入 中,
得: ,解得: ,
∴ 2+2×(-2)=-2,
故答案为:-2.
【分析】先将点A、B代入反比例函数 中求得k、m值,再将点A、B代入一次函数 中求得a、b,代入代数式中解之即可.
12.(2020·达县)如图,点A、B在反比函数 的图象上,A、B的纵坐标分别是3和6,连接 、 ,则 的面积是________.
【答案】 9
【考点】反比例函数系数k的几何意义
【解析】【解答】如图,
设BD⊥y轴于点D,AC⊥y轴于点C,AC与OB的交点为点E,
∵A、B的纵坐标分别是3和6,
代入函数关系式可得横坐标分别为4,2;
∴A(4,3),B(2,6);
∴AC=4,BD=2,CD=3
由反比例函数的几何意义可得S△BOD=S△AOC ,
∴S四边形EBDC=S△AOE ,
∴S△AOB=S四边形ABDC= ,
故答案为:9.
【分析】设BD⊥y轴于点D,AC⊥y轴于点C,AC与OB的交点为点E,证得S四边形EBDC=S△AOE即可得S△AOB=S四边形ABDC , 根据梯形的面积公式求解即可.
13.(2020·沈阳)如图,在平面直角坐标系中,O是坐标原点,在 中, 于点C,点A在反比例函数 的图象上,若OB=4,AC=3,则k的值为________.
【答案】 6
【考点】待定系数法求反比例函数解析式
【解析】【解答】解:∵AO=OB
∴△AOB为等腰三角形
又∵AC⊥OB
∴C为OB中点
∵OB=4,AC=3
∴C(2,0),A(2,3)
将A点坐标代入反比例函数 得,3=
∴k=6
故答案为:6.
【分析】由等腰三角形的性质可得C点坐标,结合AC长即可得到A点坐标,进而可得k值.
14.(2018·安顺)如图,已知直线 与x轴、y轴相交于P、Q两点,与 的图象相交于 、 两点,连接OA、OB.给出下列结论:① ;② ;③ ;④不等式 的解集是 或 .
其中正确结论的序号是________.
【答案】②③④
【考点】反比例函数与一次函数的交点问题
【解析】【解答】解:由图象知,k1<0,k2<0,∴k1k2>0,故①错误;
把A(-2,m)、B(1,n)代入y= 中得-2m=n,
∴m+ n=0,故②正确;
把A(-2,m)、B(1,n)代入y=k1x+b得
,
∴ ,
∵-2m=n,
∴y=-mx-m,
∵已知直线y=k1x+b与x轴、y轴相交于P、Q两点,
∴P(-1,0),Q(0,-m),
∴OP=1,OQ=m,
∴S△AOP= m,S△BOQ= m,
∴S△AOP=S△BOQ;故③正确;
由图象知不等式k1x+b> 的解集是x<-2或0<x<1,故④正确;
故答案为:②③④.
【分析】一次函数的图像与双曲线的图像都经过二,四象限,故,k1<0,k2<0,k1k2>0;把A(-2,m)、B(1,n)分别代入双曲线的解析式,根据双曲线k的几何意义得出-2m=n,,故m+ n=0;把A(-2,m)、B(1,n)两点的坐标分别代入直线解析式,用含m,n的式子表示出k1,b再根据-2m=n,得出y=-mx-m,根据直线与坐标轴交点的坐标特点得出P,Q两点的坐标,得出OP,OQ的长,从而根据三角形的面积公式得出S△AOP=S△BOQ;根据图像求不等式k1x+b> k 2 x 的解集,就是求直线的图像在反比例函数的图像的上方时,相应的自变量的取值,注意反比例函数的图像不能与坐标轴相交这一限制条件,即可得出答案。
15.(2019·郴州)如图,点A,C分别是正比例函数 的图象与反比例函数 的图象的交点,过A点作 轴于点D,过C点作 轴于点B,则四边形ABCD的面积为________.
【答案】 8
【考点】反比例函数图象的对称性,反比例函数与一次函数的交点问题
【解析】【解答】 A、C是两函数图象的交点,
A、C关于原点对称,
轴, 轴,
, ,
,
又 反比例函数 的图象上,
,
,
故答案为:8.
【分析】根据点A和点C分别为两个函数的交点,即可德达两个点关于原点对称,从而得到线段对应相等,根据三角形的面积的计算公式进行求解即可。
模拟预测
1.(2020·温州模拟)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压 与气体体积 之间的函数关系如图所示.当气球的体积是 ,气球内的气压是( ) .
A. 96 B. 150 C. 120 D. 64
【答案】 A
【考点】反比例函数的实际应用
【解析】【解答】设球内气体的气压p(kPa)和气体体积V(m3)的关系式为 ,
∵图象过点(0.8,120)
∴k=96,
即气压p(kPa)与气体体积V(m3)之间的函数关系为 ,
∴当V=1时,p=96.
故答案为:A.
【分析】根据题意可知温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,且过点(0.8,120),代入解析式即可得到结论.
2.(2020·武汉模拟)反比例函数y= 的图象上有三点(x1 , ﹣1),B(x2 , a),C(x3 , 3),当x3<x2<x1时,a的取值范围为( )
A. a>3 B. a<﹣1 C. ﹣1<a<3 D. a>3或a<﹣1
【答案】 D
【考点】反比例函数的性质,反比例函数图象上点的坐标特征
【解析】【解答】解:∵k=﹣2<0,
∴函数图象在二、四象限,在每个象限内y随x的增大而增大,
∵A(x1 , ﹣1),C(x3 , 3),
∴A(x1 , ﹣1)在第四象限,C(x3 , 3)在第二象限,
∴x1>0,x3<0,
当x3<x2<0时,则a>3,
当0<x2<x1时,则a<﹣1,
故a的取值范围为a>3或a<﹣1,
故答案为:D.
【分析】观察反比例函数的解析式可知k=﹣2<0,由反比例函数的图像和性质知函数图象在二、四象限,且在每个象限内y随x的增大而增大,结合各点的横坐标即可判断求解.
3.(2020·武汉模拟)如图直线y1=x+1与双曲线y2= 交于A (2,m)、B(﹣3,n)两点.则当y1>y2时,x的取值范围是( )
A. x>﹣3或0<x<2 B. ﹣3<x<0或x>2 C. x<﹣3或0<x<2 D. ﹣3<x<2
【答案】 B
【考点】反比例函数与一次函数的交点问题
【解析】【解答】根据图象可得当y1>y2时,x的取值范围是:﹣3<x<0或x>2.
故答案为:B.
【分析】当y1>y2时,x的取值范围就是y1的图象落在y2图象的上方时对应的x的取值范围.
4.(2020·江阴模拟)如图,▱OABC的周长为7,∠AOC=60°,以O为原点,OC所在直线为x轴建立直角坐标系,函数 (x>0)的图像经过▱OABC的顶点A和BC的中点M,则k的值为( )
A. B. 12 C. D. 6
【答案】 C
【考点】反比例函数与一次函数的交点问题,反比例函数图象上点的坐标特征
【解析】【解答】解:作AD⊥x轴于D,MN⊥x轴于N,
∵四边形OABC是平行四边形,
∴OA=BC,AB=OC,OA∥BC,
∴∠BCN=∠AOC=60°.
设OA=a,由▱OABC的周长为7,
∴OC= -a,
∵∠AOC=60°, ,
,
∵M是BC的中点,BC=OA=a,∴CM= a,
又∠MCN=60°,
,
∴ON=OC+CN= ,
,
∵点A,M都在反比例函数 的图象上,
,解得a=2,
,
.
故答案为:C.
【分析】作AD⊥x轴于D,MN⊥x轴于N,设OA=a,根据题意得到OC= -a,解直角三角形表示出A、M的坐标,根据反比例函数图象上点的坐标特征得到关于a的方程,解得a,求得A的坐标,即可求得k的值.
5.(2020·铜仁模拟)如图所示,已知A( ,y1),B(2,y2)为反比例函数 图像上的两点,动点P(x,0)在x正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
A. ( ,0) B. (1,0) C. ( ,0) D. ( ,0)
【答案】 D
【考点】反比例函数与一次函数的交点问题
【解析】【解答】解:∵把A( ,y1),B(2,y2)代入反比例函数y= 得:y1=2,y2= ,
∴A( ,2),B(2, ),
∵在△ABP中,由三角形的三边关系定理得:|AP-BP|<AB,
∴延长AB交x轴于P′,当P在P′点时,PA-PB=AB,
即此时线段AP与线段BP之差达到最大,
设直线AB的解析式是y=kx+b,
把A、B的坐标代入得:
,
解得:k=-1,b= ,
∴直线AB的解析式是y=-x+ ,
当y=0时,x= ,
即P( ,0),
故答案为:D.
【分析】求出A、B的坐标,设直线AB的解析式是y=kx+b,把A、B的坐标代入求出直线AB的解析式,根据三角形的三边关系定理得出在△ABP中,|AP-BP|<AB,延长AB交x轴于P′,当P在P′点时,PA-PB=AB,此时线段AP与线段BP之差达到最大,求出直线AB于x轴的交点坐标即可.
6.(2020·泰州模拟)若反比例函数 的图象经过第一、三象限,则 k的取值范围是________.
【答案】 k<
【考点】反比例函数的性质
【解析】【解答】解:由题意得: ,则
故答案为: .
【分析】根据反比例函数的图像“当k>0时,图像分布在一、三象限”可得关于k的不等式,解这个不等式即可求解.
7.(2020·江都模拟)若双曲线 与直线 无交点,则k的取值范围是________.
【答案】 k>-1
【考点】反比例函数与一次函数的交点问题
【解析】【解答】解:∵双曲线 与直线y=-3x无交点,
∴k-1与-3异号,
∴k-1>0,
∴k>1,
故答案为: .
【分析】由双曲线 与直线y=-3x无交点,于是得到k-1与-3异号,解不等式即可得到k的取值范围.
8.(2020·丰台模拟)如图,正比例函数 的图象和反比例函数 的图象交于A,B两点,分别过点A,B作 轴的垂线,垂足为点C,D,则△ 与 的面积之和为________.
【答案】 1
【考点】反比例函数的性质,反比例函数系数k的几何意义
【解析】【解答】解: 正比例函数 的图象和反比例函数 的图象交于A,B两点,
关于原点成中心对称,
,垂足分别为
故答案为1.
【分析】由 关于原点成中心对称,反比例函数的系数的几何意义可得答案.
9.(2020·铜川模拟)如图, 的三个顶点分别为 .若反比例函数 在第一象限内的图象与 有交点,则 的取值范围是________.
【答案】 2≤k≤16
【考点】反比例函数图象上点的坐标特征
【解析】【解答】解:当交点为A点时,将A点代入函数解析式,求得k=4;
当交点为C点时,将C点代入函数解析式,求得k=16,
故当函数与三角形有交点时,k的取值范围为2≤k≤16.
故答案为:2≤k≤16.
【分析】根据A、B、C的坐标,可得△ABC是直角三角形,从而可知当反比例函数 经过点A时k最小,经过点C时k最大,将点A、C的坐标分别代入中求出k值,从而求出结论.
10.(2020·阜宁模拟)如图,在平面直角坐标系中,反比例函数 与正比例函数 的图像分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
【答案】 3
【考点】反比例函数与一次函数的交点问题
【解析】【解答】解:如图,过B作BD⊥x轴于点D,过A作AC⊥y轴于点C.
设点A横坐标为a(a>0),则A ,
∵A在正比例函数y=kx图象上
∴ ,
∴ ,
同理,设点B横坐标为b(b>0),则B
∴ ,
∴k= ,
∴ ,
∴ab=3,
∴当点A坐标为 时,点B坐标为
∴OC=OD,
将△AOC绕点O顺时针旋转90°,得到△ODA′,
∵BD⊥x轴,
∴B、D、A′共线,
∵∠AOB=45°,∠AOA′=90°,
∴∠BOA′=45°,
∵OA=OA′,OB=OB,
∴△AOB≌△A′OB,
∵S△BOD=S△AOC=3× = ,
∴S△AOB=S△A'OB=3.
故答案为:3.
【分析】根据A、B两点分别在反比例函数和正比例函数图象上,且存在相同k值,可先证明点A横坐标和B纵坐标相等,利用旋转知识证明△AOB≌△A′OB,进而根据全等三角形的性质得出△AOB面积=△A′OB的面积,再利用反比例函数k的几何意义即可解决问题.
考点07 分式—2021年《三步冲刺中考•数学》(全国通用)之第1步小题夯基础(原卷+解析): 这是一份考点07 分式—2021年《三步冲刺中考•数学》(全国通用)之第1步小题夯基础(原卷+解析),共18页。
考点36 概率—2021年《三步冲刺中考•数学》(全国通用)之第1步小题夯基础(原卷+解析): 这是一份考点36 概率—2021年《三步冲刺中考•数学》(全国通用)之第1步小题夯基础(原卷+解析),共19页。
考点35 统计—2021年《三步冲刺中考•数学》(全国通用)之第1步小题夯基础(原卷+解析): 这是一份考点35 统计—2021年《三步冲刺中考•数学》(全国通用)之第1步小题夯基础(原卷+解析),共19页。












