考点22 等腰三角形与等边三角形—2021年《三步冲刺中考•数学》（全国通用）之第1步小题夯基础（原卷+解析）

这是一份考点22 等腰三角形与等边三角形—2021年《三步冲刺中考•数学》（全国通用）之第1步小题夯基础（原卷+解析），共34页。试卷主要包含了条．等内容，欢迎下载使用。

第一步 小题夯基础


考点22 等腰三角形与等边三角形 真题回顾



1.（2020·呼伦贝尔）如图， 的垂直平分线 交 于点D，若 ，则 的度数是（    ）

A. 25°                                       B. 20°                                       C. 30°                                       D. 15°
2.（2019·南充）如图，在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，若BC=6，AC=5，则△ACE的周长为（    ）

A. 8                                         B. 11                                         C. 16                                         D. 17
3.（2020·南充）如图，在等腰三角形ABC中，BD为∠ABC的平分线，∠A=36°，AB=AC=a，BC=b，则CD=（   ）

A.                                     B.                                     C. a-b                                    D. b-a
4.（2019·苏州）如图，在△ABC中，点D在BC上，AB=AD=DC，∠B=80°，则∠C的度数为（   ）

A. 30°                                       B. 40°                                       C. 45°                                       D. 60°
5.（2018·雅安）如图所示，底边BC为2 ，顶角A为120°的等腰△ABC中，DE垂直平分AB于D，则△ACE的周长为（  ）

A. 2+2                                    B. 2+                                    C. 4                                   D. 3
6. （2019·连云港）如图，在Rt△ACB中，∠C=90°，BE平分∠ABC，ED垂直平分AB于D．若AC=9，则AE的值是（　　）

A. 6                                        B. 4                                        C. 6                                        D. 4
7.（2017·海南）已知△ABC的三边长分别为4、4、6，在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画（   ）条．
A. 3                                           B. 4                                           C. 5                                           D. 6
8.（2018·镇江）边长为a的等边三角形，记为第1个等边三角形，取其各边的三等分点，顺次连接得到一个正六边形，记为第1个正六边形，取这个正六边形不相邻的三边中点，顺次连接又得到一个等边三角形，记为第2个等边三角形，取其各边的三等分点，顺次连接又得到一个正六边形，记为第2个正六边形（如图），…，按此方式依次操作，则第6个正六边形的边长为（   ）
A.                          B.                          C.                          D. 
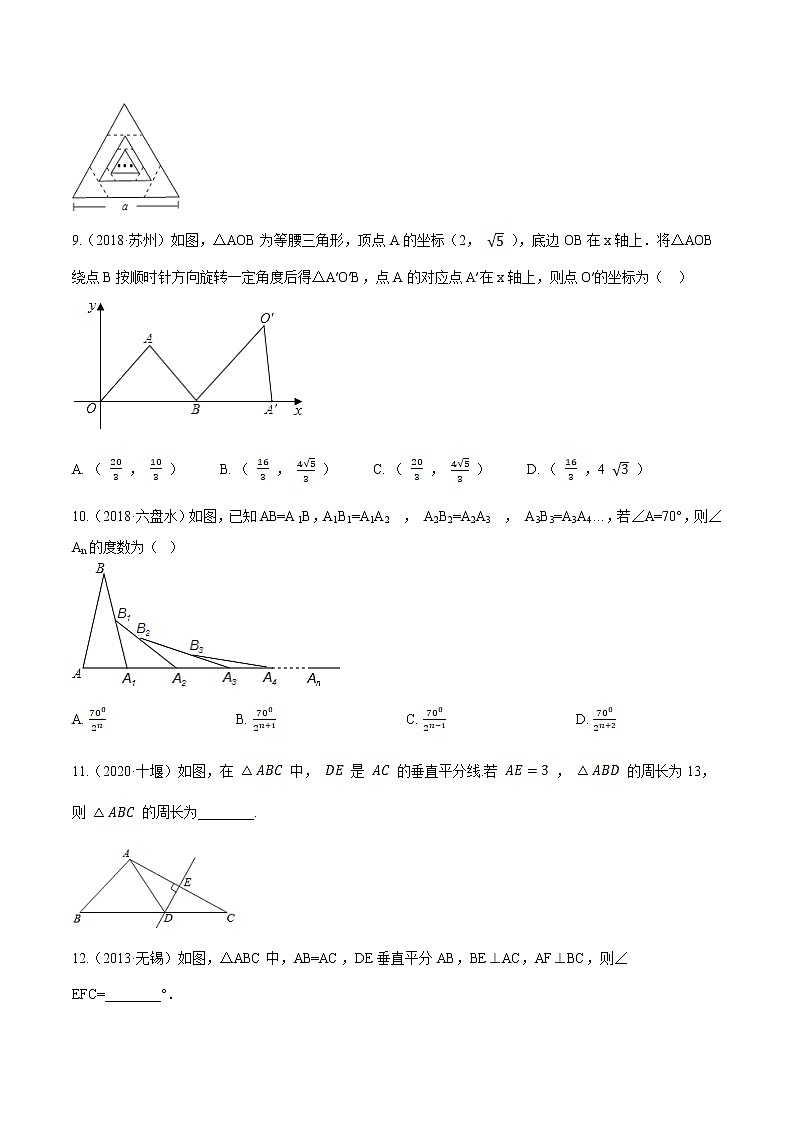
9.（2018·苏州）如图，△AOB为等腰三角形，顶点A的坐标（2， ），底边OB在x轴上．将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B，点A的对应点A′在x轴上，则点O′的坐标为（   ）

A. （ ， ）          B. （ ， ）          C. （ ， ）          D. （ ，4 ）
10.（2018·六盘水）如图，已知AB=A1B，A1B1=A1A2 ， A2B2=A2A3 ， A3B3=A3A4…，若∠A=70°，则∠An的度数为（  ）

A.                                      B.                                      C.                                      D. 
11.（2020·十堰）如图，在 中， 是 的垂直平分线.若 ， 的周长为13，则 的周长为________.

12.（2013·无锡）如图，△ABC中，AB=AC，DE垂直平分AB，BE⊥AC，AF⊥BC，则∠EFC=________°．

13.（2018·株洲）如图，在平行四边形ABCD中，连接BD，且BD＝CD，过点A作AM⊥BD于点M，过点D作DN⊥AB于点N，且DN＝ ，在DB的延长线上取一点P，满足∠ABD＝∠MAP＋∠PAB，则AP＝________.

14.（2019·番禺模拟）如图，△ABC为等边三角形，AB=2．若P为△ABC内一动点，且满足∠PAB=∠ACP ， 则线段PB长度的最小值为________．

15.（2017·抚顺）如图，等边△A1C1C2的周长为1，作C1D1⊥A1C2于D1 ， 在C1C2的延长线上取点C3 ， 使D1C3=D1C1 ， 连接D1C3 ， 以C2C3为边作等边△A2C2C3；作C2D2⊥A2C3于D2 ， 在C2C3的延长线上取点C4 ， 使D2C4=D2C2 ， 连接D2C4 ， 以C3C4为边作等边△A3C3C4；…且点A1 ， A2 ， A3 ， …都在直线C1C2同侧，如此下去，则△A1C1C2 ， △A2C2C3 ， △A3C3C4 ， …，△AnCnCn+1的周长和为________．（n≥2，且n为整数）

模拟预测


1.（2020·杭州模拟）如图，△ABC是等边三角形，AD是BC边上的高，点E是AC边的中点，点P是AD上的一个动点，当PC+PE最小时，∠CPE的度数是（　　）

A. 30°                                       B. 45°                                       C. 60°                                       D. 90°
2.（2020·西安模拟）如图， 内有一点 ， 平分 ， ， ，若 ， ，则 等于（   ）

A. 1                                         B.                                          C. 2                                         D. 
3.（2019·桥东模拟）在等腰△ABC中，AB=AC，D、E分别是BC，AC的中点，点P是线段AD上的一个动点，当△PCE的周长最小时，P点的位置在△ABC的（   ）

A. 重心                                  B. 内心                                  C. 外心                                  D. 不能确定
4.（2017·游仙模拟）如图，在△ABC中，AB=AC，∠A=120°，BC=6cm，AB的垂直平分线交BC于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F，则MN的长为（   ）
A. 4cm                                     B. 3cm                                     C. 2cm                                     D. 1cm
5.（2019·兰州模拟）如图，坐标平面内一点A(2，－1)，O为原点，P是x轴上的一个动点，如果以点P、O、A为顶点的三角形是等腰三角形，那么符合条件的动点P的个数为   (       )

A. 2                                           B. 3                                           C. 4                                           D. 5
6.（2020·三明模拟）如图，在△ABC中，AB=20cm，AC=12cm，点P从点B出发以每秒3cm的速度向点A运动，点Q从点A同时出发以每秒2cm的速度向点C运动，其中一个动点到达端点时，另一个动点也随之停止运动，当△APQ是等腰三角形时，运动的时间是  （   ）

A. 2.5                                      B. 3秒                                      C. 3.5秒                                      D. 4秒
7.（2017·资中模拟）如图，已知等腰△ABC中，AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，下面的结论：①∠APO+∠DCO=30°；②△OPC是等边三角形；③AC=AO+AP；④S△ABC=S四边形AOCP ， 其中正确的个数是（   ）

A. 1                                           B. 2                                           C. 3                                           D. 4
8.（2020·柘城模拟）如图，等腰 中， ， ，点 是边 上不与点 ， 重合的一个动点，直线 垂直平分 ，垂足为 ，当 是直角三角形时， 的长为________.

9.（2017·黄冈模拟）如图，在△ABC中，∠ACB=90°，AC=6cm，BC=8cm，动点P从点C出发，按C→B→A的路径，以2cm每秒的速度运动，设运动时间为t秒，当t为________时，△ACP是等腰三角形．

10.（2017·黄岛模拟）如图放置的△OAB1 ， △B1A1B2 ， △B2A2B3 ， …都是边长为2的等边三角形，点A在x轴上，点O，B1 ， B2 ， B3 ， …都在正比例函数y=kx的图象l上，则点B2017的坐标是________．


第一步 小题夯基础


考点22 等腰三角形与等边三角形 真题回顾



1.（2020·呼伦贝尔）如图， 的垂直平分线 交 于点D，若 ，则 的度数是（    ）

A. 25°                                       B. 20°                                       C. 30°                                       D. 15°
【答案】 D
【考点】线段垂直平分线的性质，等腰三角形的性质
【解析】【解答】解：∵AB=AC，∠C=∠ABC=65°，
∴∠A=180°-65°×2=50°，
∵MN垂直平分AB，
∴AD=BD，
∴∠A=∠ABD=50°，
∴∠DBC=∠ABC-∠ABD=15°，
故答案为：D．
【分析】根据等要三角形的性质得到∠ABC，再根据垂直平分线的性质求出∠ABD，从而可得结果．
2.（2019·南充）如图，在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，若BC=6，AC=5，则△ACE的周长为（    ）

A. 8                                         B. 11                                         C. 16                                         D. 17
【答案】 B
【考点】线段垂直平分线的性质
【解析】【解答】
解：∵DE垂直平分AB，
∴AE=BE，
∴△ACE的周长=AC+CE+AE
=AC+CE+BE
=AC+BC
=5+6
=11．
故答案为：B．
【分析】根据线段垂直平分线的性质可得AE=BE，则△ACE的周长=EC+AE+AC=BC+AC，因而得解。
3.（2020·南充）如图，在等腰三角形ABC中，BD为∠ABC的平分线，∠A=36°，AB=AC=a，BC=b，则CD=（   ）

A.                                     B.                                     C. a-b                                    D. b-a
【答案】 C
【考点】等腰三角形的判定与性质
【解析】【解答】解：∵在等腰△ABC中，BD为∠ABC的平分线，∠A=36°，
∴∠ABC=∠C=2∠ABD=72°，
∴∠ABD=36°=∠A，
∴BD=AD，
∴∠BDC=∠A+∠ABD=72°=∠C，
∴BD=BC，
∵AB=AC=a，BC=b，
∴CD=AC-AD=a-b，
故答案为：C．
【分析】根据等腰三角形的性质和判定得出BD=BC=AD，进而解答即可．
4.（2019·苏州）如图，在△ABC中，点D在BC上，AB=AD=DC，∠B=80°，则∠C的度数为（   ）

A. 30°                                       B. 40°                                       C. 45°                                       D. 60°
【答案】 B
【考点】等腰三角形的性质
【解析】【解答】解：∵△ABD中，AB=AD，∠B=80°，
∴∠B=∠ADB=80°，
∴∠ADC=180°﹣∠ADB=100°，
∵AD=CD，
∴∠C= = =40°．
故选：B．
【分析】先根据等腰三角形的性质求出∠ADB的度数，再由平角的定义得出∠ADC的度数，根据等腰三角形的性质即可得出结论．
5.（2018·雅安）如图所示，底边BC为2 ，顶角A为120°的等腰△ABC中，DE垂直平分AB于D，则△ACE的周长为（  ）

A. 2+2                                    B. 2+                                    C. 4                                   D. 3
【答案】 A
【考点】线段垂直平分线的性质，等腰三角形的性质
【解析】【解答】解：过A作AF⊥BC于F，
∵AB=AC，∠A=120°，
∴∠B=∠C=30°，
∴AB=AC=2，
∵DE垂直平分AB，
∴BE=AE，
∴AE+CE=BC=2 ，
∴△ACE的周长=AC+AE+CE=AC+BC=2+2 ，
故选：A．

【分析】本题考查了线段垂直平分线性质，三角形的内角和定理，等腰三角形的性质，含30度角的直角三角形性质等知识点，主要考查运用性质进行推理的能力．过A作AF⊥BC于F，根据等腰三角形的性质得到∠B=∠C=30°，得到AB=AC=2，根据线段垂直平分线的性质得到BE=AE，即可得到结论．
6. （2019·连云港）如图，在Rt△ACB中，∠C=90°，BE平分∠ABC，ED垂直平分AB于D．若AC=9，则AE的值是（　　）


A. 6                                        B. 4                                        C. 6                                        D. 4
【答案】 C
【考点】线段垂直平分线的性质
【解析】【解答】解：∵BE平分∠ABC，
∴∠CBE=∠ABE，
∵ED垂直平分AB于D，
∴EA=EB，
∴∠A=∠ABE，
∴∠CBE=30°，
∴BE=2EC，即AE=2EC，
而AE+EC=AC=9，
∴AE=6．
故选C．
【分析】由角平分线的定义得到∠CBE=∠ABE，再根据线段的垂直平分线的性质得到EA=EB，则∠A=∠ABE，可得∠CBE=30°，根据含30度的直角三角形三边的关系得到BE=2EC，即AE=2EC，由AE+EC=AC=9，即可求出AC．
7.（2017·海南）已知△ABC的三边长分别为4、4、6，在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画（   ）条．
A. 3                                           B. 4                                           C. 5                                           D. 6
【答案】 B
【考点】等腰三角形的判定
【解析】【解答】解：如图所示：

当AC=CD，AB=BG，AF=CF，AE=BE时，都能得到符合题意的等腰三角形．
故选B．
【分析】根据等腰三角形的性质，利用4作为腰或底边得出符合题意的图形即可．
8.（2018·镇江）边长为a的等边三角形，记为第1个等边三角形，取其各边的三等分点，顺次连接得到一个正六边形，记为第1个正六边形，取这个正六边形不相邻的三边中点，顺次连接又得到一个等边三角形，记为第2个等边三角形，取其各边的三等分点，顺次连接又得到一个正六边形，记为第2个正六边形（如图），…，按此方式依次操作，则第6个正六边形的边长为（   ）

A.                          B.                          C.                          D. 
【答案】 A
【考点】等边三角形的判定与性质
【解析】【解答】解：连接AD、DF、DB．
∵六边形ABCDEF是正六边形，
∴∠ABC=∠BAF=∠AFE，AB=AF，∠E=∠C=120°，EF=DE=BC=CD，
∴∠EFD=∠EDF=∠CBD=∠BDC=30°，
∵∠AFE=∠ABC=120°，
∴∠AFD=∠ABD=90°，
在Rt△ABD和RtAFD中

∴Rt△ABD≌Rt△AFD（HL），
∴∠BAD=∠FAD= ×120°=60°，
∴∠FAD+∠AFE=60°+120°=180°，
∴AD∥EF，
∵G、I分别为AF、DE中点，
∴GI∥EF∥AD，
∴∠FGI=∠FAD=60°，

∵六边形ABCDEF是正六边形，△QKM是等边三角形，
∴∠EDM=60°=∠M，
∴ED=EM，
同理AF=QF，
即AF=QF=EF=EM，
∵等边三角形QKM的边长是a，
∴第一个正六边形ABCDEF的边长是  a，即等边三角形QKM的边长的 ，
过F作FZ⊥GI于Z，过E作EN⊥GI于N，
则FZ∥EN，
∵EF∥GI，
∴四边形FZNE是平行四边形，
∴EF=ZN=  a，
∵GF= AF= ×  a= a，∠FGI=60°（已证），
∴∠GFZ=30°，
∴GZ=  GF=  a，
同理IN=  a，
∴GI=  a+  a+  a=  a，即第二个等边三角形的边长是  a，与上面求出的第一个正六边形的边长的方法类似，可求出第二个正六边形的边长是 ×  a；
同理第第三个等边三角形的边长是 ×  a，与上面求出的第一个正六边形的边长的方法类似，可求出第三个正六边形的边长是 × ×  a；
同理第四个等边三角形的边长是 × ×  a，第四个正六边形的边长是 × × ×  a；
第五个等边三角形的边长是 × × ×  a，第五个正六边形的边长是 × × × ×  a；
第六个等边三角形的边长是 × × × ×  a，第六个正六边形的边长是 × × × × ×  a，
即第六个正六边形的边长是 × a，
故选：A．

【分析】连接AD、DB、DF，求出∠AFD=∠ABD=90°，根据HL证两三角形全等得出∠FAD=60°，求出AD∥EF∥GI，过F作FZ⊥GI，过E作EN⊥GI于N，得出平行四边形FZNE得出EF=ZN=  a，求出GI的长，求出第一个正六边形的边长是  a，是等边三角形QKM的边长的 ；同理第二个正六边形的边长是等边三角形GHI的边长的 ；求出第五个等边三角形的边长，乘以 即可得出第六个正六边形的边长．
9.（2018·苏州）如图，△AOB为等腰三角形，顶点A的坐标（2， ），底边OB在x轴上．将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B，点A的对应点A′在x轴上，则点O′的坐标为（   ）

A. （ ， ）          B. （ ， ）          C. （ ， ）          D. （ ，4 ）
【答案】 C
【考点】等腰三角形的性质
【解析】【解答】解：如图，过点A作AC⊥OB于C，过点O′作O′D⊥A′B于D，
∵A（2， ），
∴OC=2，AC= ，
由勾股定理得，OA= = =3，
∵△AOB为等腰三角形，OB是底边，
∴OB=2OC=2×2=4，
由旋转的性质得，BO′=OB=4，∠A′BO′=∠ABO，
∴O′D=4× = ，
BD=4× = ，
∴OD=OB+BD=4+ = ，
∴点O′的坐标为（ ， ）．
故选：C．

【分析】过点A作AC⊥OB于C，过点O′作O′D⊥A′B于D，根据点A的坐标求出OC、AC，再利用勾股定理列式计算求出OA，根据等腰三角形三线合一的性质求出OB，根据旋转的性质可得BO′=OB，∠A′BO′=∠ABO，然后解直角三角形求出O′D、BD，再求出OD，然后写出点O′的坐标即可．
10.（2018·六盘水）如图，已知AB=A1B，A1B1=A1A2 ， A2B2=A2A3 ， A3B3=A3A4…，若∠A=70°，则∠An的度数为（  ）

A.                                      B.                                      C.                                      D. 
【答案】 C
【考点】等腰三角形的性质
【解析】【解答】解：∵在△ABA1中，∠A=70°，AB=A1B，
∴∠BA1A=70°，
∵A1A2=A1B1 ， ∠BA1A是△A1A2B1的外角，
∴∠B1A2A1= =35°；
同理可得，
∠B2A3A2=17.5°，∠B3A4A3= ×17.5°= ，
∴∠An﹣1AnBn﹣1= ．
故选：C．

【分析】根据三角形外角的性质及等腰三角形的性质分别求出∠B1A2A1 ， ∠B2A3A2及∠B3A4A3的度数，找出规律即可得出∠An﹣1AnBn﹣1的度数．本题考查的是等腰三角形的性质及三角形外角的性质，根据题意得出∠B1C2A1 ， ∠B2A3A2及∠B3A4A3的度数，找出规律是解答此题的关键．
11.（2020·十堰）如图，在 中， 是 的垂直平分线.若 ， 的周长为13，则 的周长为________.

【答案】 19
【考点】线段垂直平分线的性质
【解析】【解答】解： 是 的垂直平分线. ，
 
 
的周长
 
故答案为：19
【分析】由线段的垂直平分线的性质可得 ，从而可得答案.
12.（2013·无锡）如图，△ABC中，AB=AC，DE垂直平分AB，BE⊥AC，AF⊥BC，则∠EFC=________°．

【答案】 45
【考点】线段垂直平分线的性质，等腰三角形的性质
【解析】【解答】解：∵DE垂直平分AB，
∴AE=BE，
∵BE⊥AC，
∴△ABE是等腰直角三角形，
∴∠BAE=∠ABE=45°，
又∵AB=AC，
∴∠ABC= （180°﹣∠BAC）= （180°﹣45°）=67.5°，
∴∠CBE=∠ABC﹣∠ABE=67.5°﹣45°=22.5°，
∵AB=AC，AF⊥BC，
∴BF=CF，
∵EF= BC（直角三角形斜边中线等于斜边的一半），
∴BF=EF=CF，
∴∠BEF=∠CBE=22.5°，
∴∠EFC=∠BEF+∠CBE=22.5°+22.5°=45°．
故答案为：45．

【分析】根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE，然后求出△ABE是等腰直角三角形，根据等腰直角三角形的性质求出∠BAE=∠ABE=45°，再根据等腰三角形两底角相等求出∠ABC，然后求出∠CBE，根据等腰三角形三线合一的性质可得BF=CF，根据直角三角形斜边上的中线等于斜边的一半可得BF=EF，根据等边对等角求出∠BEF=∠CBE，然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．
13.（2018·株洲）如图，在平行四边形ABCD中，连接BD，且BD＝CD，过点A作AM⊥BD于点M，过点D作DN⊥AB于点N，且DN＝ ，在DB的延长线上取一点P，满足∠ABD＝∠MAP＋∠PAB，则AP＝________.

【答案】6
【考点】等腰三角形的判定与性质
【解析】【解答】解：∵BD=CD，AB=CD，
∴BD=BA，
又∵AM⊥BD，DN⊥AB，
∴DN=AM=3 ，
又∵∠ABD=∠MAP+∠PAB，∠ABD=∠P+∠BAP，
∴∠P=∠PAM，
∴△APM是等腰直角三角形，
∴AP= AM=6，
故答案为：6．
【分析】根据平行四边形的性质及BD=CD得出BD=BA，根据等腰三角形两腰上的高相等得出DN=AM=3，根据三角形的外角的定理，及∠ABD=∠MAP+∠PAB得出∠P=∠PAM，从而判断出△APM是等腰直角三角形，根据等腰直角三角形的边之间的关系得出AP的长。
14.（2019·番禺模拟）如图，△ABC为等边三角形，AB=2．若P为△ABC内一动点，且满足∠PAB=∠ACP ， 则线段PB长度的最小值为________．

【答案】
【考点】等边三角形的性质
【解析】【解答】   是等边三角形，
  ， ，
  ，
  ，
  ，
点 的运动轨迹是 ，
当 、 、 共线时， 长度最小，设 交 于 ，如图所示：

此时 ， ，
则 ， ， ，
  ， ，
  .
故答案为： .
【分析】根据等边三角形的性质及三角形的内角和可得出∠APC=120°，可得点 的运动轨迹是 ，当 、 、 共线时， 长度最小，设 交 于 ，如图所示，此时 ， ，由等边三角形的性质，可得 ， ， ，根据解直角三角形求出PD、BD的长，利用PB=BD-PD，即可求出PB的长.
15.（2017·抚顺）如图，等边△A1C1C2的周长为1，作C1D1⊥A1C2于D1 ， 在C1C2的延长线上取点C3 ， 使D1C3=D1C1 ， 连接D1C3 ， 以C2C3为边作等边△A2C2C3；作C2D2⊥A2C3于D2 ， 在C2C3的延长线上取点C4 ， 使D2C4=D2C2 ， 连接D2C4 ， 以C3C4为边作等边△A3C3C4；…且点A1 ， A2 ， A3 ， …都在直线C1C2同侧，如此下去，则△A1C1C2 ， △A2C2C3 ， △A3C3C4 ， …，△AnCnCn+1的周长和为________．（n≥2，且n为整数）

【答案】
【考点】等边三角形的性质
【解析】【解答】∵等边△A1C1C2的周长为1，作C1D1⊥A1C2于D1 ，
∴A1D1=D1C2 ，
∴△A2C2C3的周长= △A1C1C2的周长= ，
∴△A1C1C2 ， △A2C2C3 ， △A3C3C4 ， …，△AnCnCn+1的周长分别为1， ， ，…， ，
∴△A1C1C2 ， △A2C2C3 ， △A3C3C4 ， …，△AnCnCn+1的周长和为1+ + +…+ = ．
故答案为 ．
【分析】由已知周长是等比数列，公比是,套用等比数列求和公式即可.
模拟预测


1.（2020·杭州模拟）如图，△ABC是等边三角形，AD是BC边上的高，点E是AC边的中点，点P是AD上的一个动点，当PC+PE最小时，∠CPE的度数是（　　）

A. 30°                                       B. 45°                                       C. 60°                                       D. 90°
【答案】 C
【考点】等边三角形的性质
【解析】【解答】解：如连接BE，与AD交于点P，此时PE+PC最小，

∵△ABC是等边三角形，AD⊥BC，
∴PC＝PB，
∴PE+PC＝PB+PE＝BE，
即BE就是PE+PC的最小值，
∵△ABC是等边三角形，
∴∠BCE＝60°，
∵BA＝BC，AE＝EC，
∴BE⊥AC，
∴∠BEC＝90°，
∴∠EBC＝30°，
∵PB＝PC，
∴∠PCB＝∠PBC＝30°，
∴∠CPE＝∠PBC+∠PCB＝60°，
故答案为：C.
【分析】连接BE，与AD交于点P，此时PE+PC最小.根据等腰三角形三线合一的性质可得AD垂直平分BC，从而求出PC＝PB，可得PE+PC＝PB+PE＝BE，即BE就是PE+PC的最小值.根据等边三角形的性质及先打的中点可得∠BCE＝60°，BA＝BC，AE＝EC，从而可得BE⊥AC，∠EBC＝30°，利用等边对等角可得∠PCB＝∠PBC＝30°，利用∠CPE＝∠PBC+∠PCB即可求出结论.
2.（2020·西安模拟）如图， 内有一点 ， 平分 ， ， ，若 ， ，则 等于（   ）

A. 1                                         B.                                          C. 2                                         D. 
【答案】 A
【考点】等腰三角形的判定与性质
【解析】【解答】解：延长AD交BC于点E

∵CD平分∠ACB，AE⊥CD，
∴AC=CE.
又∵∠B=∠BAE，
∴AE=BE.
∴AD= AE= BE= (BC−AC).
∵BC=5，AC=3，
∴AD= (5−3)=1.
故答案为：A.
【分析】延长AD交BC于点E，由已知条件判定△AEC为等腰三角形，且AC=CE；由等角对等边判定AE=BE，则易求 .
3.（2019·桥东模拟）在等腰△ABC中，AB=AC，D、E分别是BC，AC的中点，点P是线段AD上的一个动点，当△PCE的周长最小时，P点的位置在△ABC的（   ）

A. 重心                                  B. 内心                                  C. 外心                                  D. 不能确定
【答案】 A
【考点】等腰三角形的性质
【解析】【解答】连接BP，根据题意可知，三角形ABC为等腰三角形
∵D为底边的中点
∴AD⊥BC
∴PB=PC
∴三角形PCE的周长=PE+PC+EC=PE+PB+EC
即点B，P，E三点共线时，距离最短，周长最小
∴BE为三角形的重心。
故答案为：A。
【分析】连接BP，根据等腰三角形的三线合一即可得到AD是线段BC的垂直平分线，根据三角形的周长公式以及两点之间线段最短，即可求得答案。
4.（2017·游仙模拟）如图，在△ABC中，AB=AC，∠A=120°，BC=6cm，AB的垂直平分线交BC于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F，则MN的长为（   ）

A. 4cm                                     B. 3cm                                     C. 2cm                                     D. 1cm
【答案】C
【考点】线段垂直平分线的性质，等边三角形的判定与性质
【解析】【解答】解：
连接AM、AN、过A作AD⊥BC于D，
∵在△ABC中，AB=AC，∠A=120°，BC=6cm，
∴∠B=∠C=30°，BD=CD=3cm，
∴AB= =2 cm=AC，
∵AB的垂直平分线EM，
∴BE= AB= cm
同理CF= cm，
∴BM= =2cm，
同理CN=2cm，
∴MN=BC﹣BM﹣CN=2cm，
故选C．
【分析】连接AM、AN、过A作AD⊥BC于D，求出AB、AC值，求出BE、CF值，求出BM、CN值，代入MN=BC﹣BM﹣CN求出即可．
5.（2019·兰州模拟）如图，坐标平面内一点A(2，－1)，O为原点，P是x轴上的一个动点，如果以点P、O、A为顶点的三角形是等腰三角形，那么符合条件的动点P的个数为   (       )

A. 2                                           B. 3                                           C. 4                                           D. 5
【答案】 C
【考点】等腰三角形的判定
【解析】【分析】根据题意，结合图形，分两种情况讨论：①OA为等腰三角形底边；②OA为等腰三角形一条腰．

【解答】如上图：①OA为等腰三角形底边，符合符合条件的动点P有一个；
②OA为等腰三角形一条腰，符合符合条件的动点P有三个．
综上所述，符合条件的点P的个数共4个．
故选C．
【点评】本题考查了等腰三角形的判定及坐标与图形的性质；利用等腰三角形的判定来解决实际问题，其关键是根据题意，画出符合实际条件的图形，再利用数学知识来求解．
6.（2020·三明模拟）如图，在△ABC中，AB=20cm，AC=12cm，点P从点B出发以每秒3cm的速度向点A运动，点Q从点A同时出发以每秒2cm的速度向点C运动，其中一个动点到达端点时，另一个动点也随之停止运动，当△APQ是等腰三角形时，运动的时间是  （   ）


A. 2.5                                      B. 3秒                                      C. 3.5秒                                      D. 4秒
【答案】 D
【考点】等腰三角形的性质
【解析】
【分析】设运动的时间为x，则AP=20-3x，当APQ是等腰三角形时，AP=AQ，则20-3x=2x，解得x即可．
【解答】设运动的时间为x，
在△ABC中，AB=20cm，AC=12cm，
点P从点B出发以每秒3cm的速度向点A运动，点Q从点A同时出发以每秒2cm的速度向点C运动，
当△APQ是等腰三角形时，AP=AQ，
AP=20-3x，AQ=2x
即20-3x=2x，
解得x=4．
故选D．
【点评】此题主要考查学生对等腰三角形的性质这一知识点的理解和掌握，此题涉及到动点，有一定的拔高难度，属于中档题．
7.（2017·资中模拟）如图，已知等腰△ABC中，AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，下面的结论：①∠APO+∠DCO=30°；②△OPC是等边三角形；③AC=AO+AP；④S△ABC=S四边形AOCP ， 其中正确的个数是（   ）

A. 1                                           B. 2                                           C. 3                                           D. 4
【答案】D
【考点】线段垂直平分线的性质，等腰三角形的性质，等边三角形的判定与性质
【解析】【解答】解：如图1，连接OB，

∵AB=AC，AD⊥BC，
∴BD=CD，∠BAD= ∠BAC= ×120°=60°，
∴OB=OC，∠ABC=90°﹣∠BAD=30°
∵OP=OC，
∴OB=OC=OP，
∴∠APO=∠ABO，∠DCO=∠DBO，
∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°；
故①正确；
∵∠APC+∠DCP+∠PBC=180°，
∴∠APC+∠DCP=150°，
∵∠APO+∠DCO=30°，
∴∠OPC+∠OCP=120°，
∴∠POC=180°﹣（∠OPC+∠OCP）=60°，
∵OP=OC，
∴△OPC是等边三角形；
故②正确；
如图2，在AC上截取AE=PA，

∵∠PAE=180°﹣∠BAC=60°，
∴△APE是等边三角形，
∴∠PEA=∠APE=60°，PE=PA，
∴∠APO+∠OPE=60°，
∵∠OPE+∠CPE=∠CPO=60°，
∴∠APO=∠CPE，
∵OP=CP，
在△OPA和△CPE中，
，
∴△OPA≌△CPE（SAS），
∴AO=CE，
∴AC=AE+CE=AO+AP；
故③正确；
如图3，过点C作CH⊥AB于H，

∵∠PAC=∠DAC=60°，AD⊥BC，
∴CH=CD，
∴S△ABC= AB•CH，
S四边形AOCP=S△ACP+S△AOC= AP•CH+ OA•CD= AP•CH+ OA•CH= CH•（AP+OA）= CH•AC，
∴S△ABC=S四边形AOCP；
故④正确．
故选D．
【分析】①利用等边对等角，即可证得：∠APO=∠ABO，∠DCO=∠DBO，则∠APO+∠DCO=∠ABO+∠DBO=∠ABD，据此即可求解；
②证明∠POC=60°且OP=OC，即可证得△OPC是等边三角形；
③首先证明△OPA≌△CPE，则AO=CE，AC=AE+CE=AO+AP．
④过点C作CH⊥AB于H，根据S四边形AOCP=S△ACP+S△AOC ， 利用三角形的面积公式即可求解．
8.（2020·柘城模拟）如图，等腰 中， ， ，点 是边 上不与点 ， 重合的一个动点，直线 垂直平分 ，垂足为 ，当 是直角三角形时， 的长为________.

【答案】 2或
【考点】线段垂直平分线的性质，等腰三角形的性质
【解析】【解答】解：①当∠AFC=90°时，AF⊥BC，

∵AB=AC，
∴BF= BC=4
∵DE垂直平分BF，
∴BD= BF=2；
②当∠CAF=90°时，过点A作AM⊥BC于点M，

∵AB=AC，
∴BM=CM，
在Rt△AMC与Rt△FAC中，∠AMC=∠FAC=90°，∠C=∠C，
∴△AMC∽△FAC，
∴
∵AC=10，MC= BC=4，
∴
∴BF=BC-FC=
∴BD= BF= .
故答案为2或 .
【分析】分两种情况讨论：①当∠AFC=90°时，AF⊥BC，利用等腰三角形的三线合一性质和垂直平分线的性质可解；②当∠CAF=90°时，过点A作AM⊥BC于点M，证明△AMC∽△FAC，列比例式求出FC，从而得BF，再利用垂直平分线的性质得BD.
9.（2017·黄冈模拟）如图，在△ABC中，∠ACB=90°，AC=6cm，BC=8cm，动点P从点C出发，按C→B→A的路径，以2cm每秒的速度运动，设运动时间为t秒，当t为________时，△ACP是等腰三角形．
【答案】3或6或6.5或5.4
【考点】等腰三角形的判定
【解析】【解答】解：∵AC=6，BC=8， ∴由勾股定理可知：AB=10，
当点P在CB上运动时，
由于∠ACP=90°，
∴只能有AC=CP，如图1，

∴CP=6，
∴t= =3，
当点P在AB上运动时，①AC=AP时，如图2，

∴AP=6，PB=AB﹣CP=10﹣6=4，
∴t= =6，②当AP=CP时，如图3，

此时点P在线段AC的垂直平分线上，
过点P作PD⊥AC于点D，
∴CD= AC=3，PD是△ACB的中位线，
∴PD= BC=4，
∴由勾股定理可知：AP=5，
∴PB=5，
∴t= =6.5；③AC=PC时，如图4，

过点C作CF⊥AB于点F，
∴cos∠A= = ，
∴AF=3.6，
∴AP=2AF=7.2，
∴PB=10﹣7.2=2.8，
∴t= =5.4；
综上所述，当t为3或6或6.5或5.4时，△ACP是等腰三角形．
故答案为：3或6或6.5或5.4．
【分析】由于没有说明哪一条边是腰，故需要分情况讨论．
10.（2017·黄岛模拟）如图放置的△OAB1 ， △B1A1B2 ， △B2A2B3 ， …都是边长为2的等边三角形，点A在x轴上，点O，B1 ， B2 ， B3 ， …都在正比例函数y=kx的图象l上，则点B2017的坐标是________．

【答案】（2017，2017 ）
【考点】等边三角形的性质
【解析】【解答】解：∵△OAB1 ， △B1A1B2 ， △B2A2B3 ， …都是边长为2的等边三角形， ∴OB1=B1B2=B2B3=…=2，且直线l的解析式为y= x，
∴B1（1， ），B2（2，2 ），B3（3，3 ），…，
∴Bn（n， n），
∴B2017（2017，2017 ）．
故答案为：（2017，2017 ）．
【分析】根据等边三角形的性质可得出OB1=B1B2=B2B3=…=2、且直线l的解析式为y= x，进而可得出点B1、B2、B3、…的坐标，根据坐标的变化即可得出变化规律“Bn（n， n）”，依此规律即可得出结论．