考点34 与圆有关的计算—2021年《三步冲刺中考•数学》（全国通用）之第1步小题夯基础（原卷+解析）

这是一份考点34 与圆有关的计算—2021年《三步冲刺中考•数学》（全国通用）之第1步小题夯基础（原卷+解析），共26页。

第一步 小题夯基础


考点34 与圆有关的计算
真题回顾



1.（2020·东营）用一个半径为 面积为 的扇形铁皮，制作一个无底的圆锥(不计损耗)，则圆锥的底面半径为（  ）
A.                                           B.                                           C. 2                                          D. 1
2.（2019·遵义）圆锥的底面半径是5cm，侧面展开图的圆心角是180°，圆锥的高是（    ）
A. 5 cm                                  B. 10cm                                  C. 6cm                                  D. 5cm
3.（2019·湖州）已知圆锥的底面半径为5cm，母线长为13cm，则这个圆锥的侧面积是（   ）
A. 60πcm2                         B. 65πcm2                             C. 120πcm2                             D. 130πcm2
4.（2019·青海）如图，在扇形 中， 为弦， ， ， ，则 的长为（    ）

A.                                       B.                                       C.                                       D. 
5.（2018·莱芜）已知圆锥的三视图如图所示，则这个圆锥的侧面展开图的面积为（   ）

A. 60πcm2                           B. 65πcm2                           C. 120πcm2                           D. 130πcm2
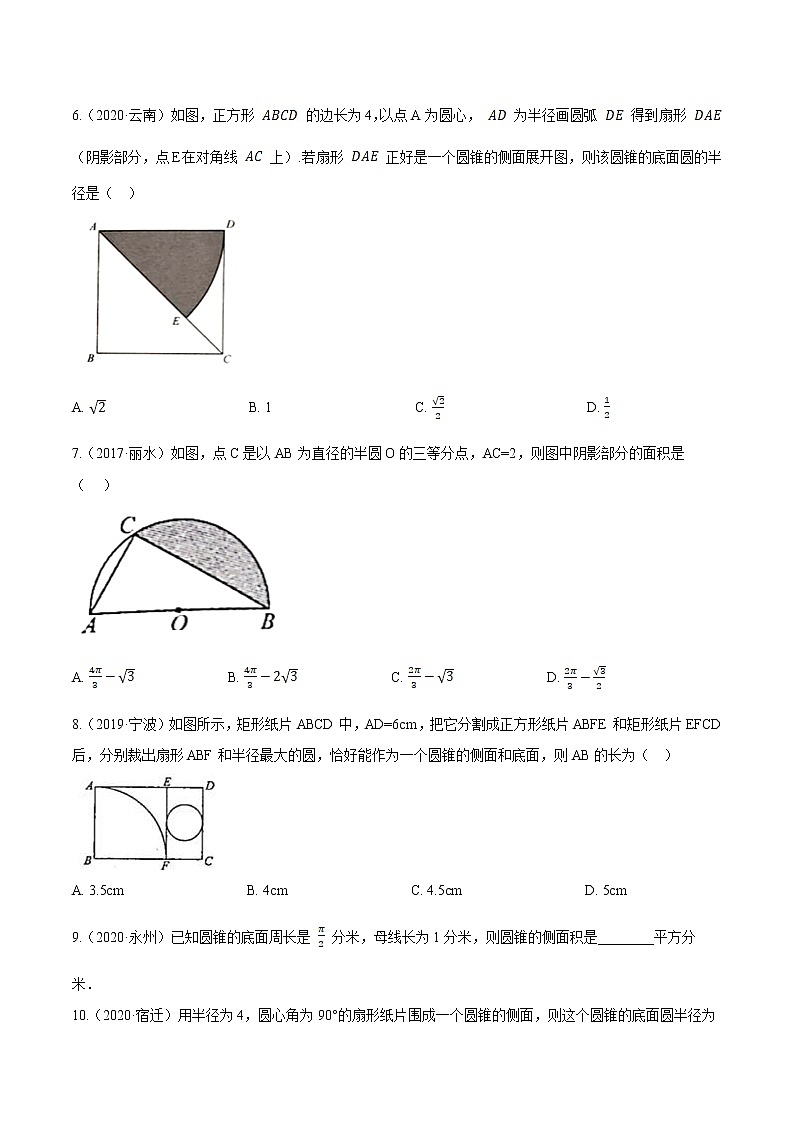
6.（2020·云南）如图，正方形 的边长为4，以点A为圆心， 为半径画圆弧 得到扇形 （阴影部分，点E在对角线 上）.若扇形 正好是一个圆锥的侧面展开图，则该圆锥的底面圆的半径是（   ）

A.                                         B. 1                                        C.                                         D. 
7.（2017·丽水）如图，点C是以AB为直径的半圆O的三等分点，AC=2，则图中阴影部分的面积是（    ）

A.                           B.                           C.                           D. 
8.（2019·宁波）如图所示，矩形纸片ABCD中，AD=6cm，把它分割成正方形纸片ABFE和矩形纸片EFCD后，分别裁出扇形ABF和半径最大的圆，恰好能作为一个圆锥的侧面和底面，则AB的长为（   ）

A. 3.5cm                                   B. 4cm                                   C. 4.5cm                                   D. 5cm
9.（2020·永州）已知圆锥的底面周长是 分米，母线长为1分米，则圆锥的侧面积是________平方分米．
10.（2020·宿迁）用半径为4，圆心角为90°的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为________.
11.（2020·黄石）如图，在 的方格纸中，每个小方格都是边长为1的正方形，其中A、B、C为格点，作 的外接圆，则 的长等于________.

12.（2020·恩施）如图，已知半圆的直径 ，点C在半圆上，以点A为圆心， 为半径画弧交 于点D，连接 .若 ，则图中阴影部分的面积为________.（结果不取近似值）

13.（2020·十堰）如图，圆心角为 的扇形 内，以 为直径作半圆，连接 .若阴影部分的面积为 ，则 ________.

14.（2020·黄冈）如图所示，将一个半径 ，圆心角 的扇形纸板放置在水平面的一条射线 上.在没有滑动的情况下，将扇形 沿射线 翻滚至 再次回到 上时，则半径 的中点P运动的路线长为________ .

15.（2018·百色）如图，把腰长为8的等腰直角三角板OAB的一直角边OA放在直线1上，按顺时针方向在l上转动两次，使得它的斜边转到l上，则直角边OA两次转动所扫过的面积为________．

模拟预测


1.（2020·荆门模拟）已知一扇形的圆心角为 ，半径为5，则以此扇形为侧面的圆锥的底面圆的周长为（   ）
A.                                       B.                                       C.                                       D. 
2.（2020·鞍山模拟）如图，菱形ABCD中，∠B＝70°，AB＝3，以AD为直径的⊙O交CD于点E，则弧DE的长为（   ）

A.  π                                     B.  π                                     C.  π                                     D.  π
3.（2020·镇海模拟）如图，5×3的网格图中，每个小正方形的边长均为1，设经过图中格点A，C，B三点的圆弧与AE交于H，则弧AH的弧长为（   ）

A.  π                              B.  π                              C.  π                              D.  π
4.（2020·绵阳模拟）如图，线段EF的长为4，O是EF的中点，以OF为边长做正方形OABC，连接AE、CF交于点P，将正方形OABC从OA与OF重合的位置开始，绕着点O逆时针旋转90°止，则点P运动的路径长为（   ）

A.                                     B.                                     C. 2π                                    D. 
5.（2020·新乡模拟）如图， ， ，以BC为直径作半圆，圆心为点O；以点C为圆心， 为半径作 ，过点O作AC的平行线交两弧于点D、E，则图中阴影部分的面积是（    ）

A.                    B.                    C.                    D. 
6.（2020·旌阳模拟）已知圆锥的高为 ，母线为 ，且 ，圆锥的侧面展开图为如图所示的扇形．将扇形沿 折叠，使A点恰好落在 上的F点，则弧长 与圆锥的底面周长的比值为（    ）

A.                                          B.                                          C.                                          D. 
7.（2020·阿城模拟）一个扇形的圆心角为 ，面积为 ，则此扇形的半径是________cm.
8.（2020·鹿城模拟）某个圆锥的侧面展开图就一个半径为6cm，圆心角为120 的扇形，则这个圆锥底面圆的半径为________
9.（2020·昆明模拟）如图，已知一块圆心角为270°的扇形铁皮，用它做一个圆锥形的烟囱帽（接缝忽略不计），圆锥底面圆的直径是60cm，则这块扇形铁皮的半径是________cm.

10.（2020·杭州模拟）如图，在半径为 ，圆心角等于45°的扇形AOB内部作一个矩形CDEF，使点C在OA上，点D、E在OB上，点F在弧AB上，且DE＝2CD，则：

（1）弧AB的长是（结果保留π）________；
（2）图中阴影部分的面积为（结果保留π）________.
第一步 小题夯基础


考点34 与圆有关的计算
真题回顾



1.（2020·东营）用一个半径为 面积为 的扇形铁皮，制作一个无底的圆锥(不计损耗)，则圆锥的底面半径为（  ）
A.                                           B.                                           C. 2                                          D. 1
【答案】 D
【考点】圆锥的计算
【解析】【解答】解：根据题意得 •2π•r•3=3π，
解得r=1．
故答案为：D．
【分析】根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形面积公式得到 •2π•r•3=3π，然后解方程即可．
2.（2019·遵义）圆锥的底面半径是5cm，侧面展开图的圆心角是180°，圆锥的高是（    ）
A. 5 cm                                  B. 10cm                                  C. 6cm                                  D. 5cm
【答案】 A
【考点】圆锥的计算
【解析】【解答】解：设圆锥的母线长为R，
根据题意得2π•5 ，
解得R＝10.
即圆锥的母线长为10cm，
∴圆锥的高为： 5 cm。
故答案为：A。
【分析】设圆锥的母线长为R，由弧长计算公式及圆锥的底面圆的周长=侧面扇形的弧长列出方程，求解算出圆锥的母线长，再根据圆锥的母线、底面圆的半径、高三线围成一个直角三角形，利用勾股定理即可算出圆锥的高。
3.（2019·湖州）已知圆锥的底面半径为5cm，母线长为13cm，则这个圆锥的侧面积是（   ）
A. 60πcm2                         B. 65πcm2                             C. 120πcm2                             D. 130πcm2
【答案】 B
【考点】圆锥的计算
【解析】【解答】解：设圆锥母线为R，圆锥底面半径为r，
∵R=13cm，r=5cm，
∴圆锥的侧面积S= ·2 r.R= ×2 ×5×13=65 （cm2）.
故答案为：B.
【分析】根据圆锥侧面展开图为扇形，再由扇形面积计算即可求得答案.
4.（2019·青海）如图，在扇形 中， 为弦， ， ， ，则 的长为（    ）

A.                                       B.                                       C.                                       D. 
【答案】 B
【考点】弧长的计算
【解析】【解答】解：连接 ，

， ，
为等边三角形，
，
，
则 的长 ，
故答案为： .
【分析】连接OC，利用有一个角是60°的等腰三角形，易证△AOC是等边三角形，利用等边三角形的每一个角是60°，求出∠AOC的度数，继而可求出∠BOC的度数；然后利用弧长公式就可求出弧BC的长。
5.（2018·莱芜）已知圆锥的三视图如图所示，则这个圆锥的侧面展开图的面积为（   ）

A. 60πcm2                           B. 65πcm2                           C. 120πcm2                           D. 130πcm2
【答案】 B
【考点】圆锥的计算
【解析】【解答】根据三视图得到圆锥的底面圆的直径为10cm，即底面圆的半径为5cm，圆锥的高为12cm，
所以圆锥的母线长= ，
所以这个圆锥的侧面积= ×2π×5×13=65π（cm2）．
故答案为：B．
【分析】根据三视图得到圆锥的底面圆的直径为10cm，即底面圆的半径为5cm，圆锥的高为12cm，根据勾股定理即可算出圆锥的母线长，再根据圆锥的侧面积等于底面周长与母线长积的一半，即可算出答案。
6.（2020·云南）如图，正方形 的边长为4，以点A为圆心， 为半径画圆弧 得到扇形 （阴影部分，点E在对角线 上）.若扇形 正好是一个圆锥的侧面展开图，则该圆锥的底面圆的半径是（   ）

A.                                         B. 1                                        C.                                         D. 
【答案】 D
【考点】圆锥的计算
【解析】【解答】解：∵正方形 的边长为4
∴
∵ 是正方形 的对角线
∴
∴
∴圆锥底面周长为 ，解得
∴该圆锥的底面圆的半径是 ，
故答案为：D.
【分析】根据题意，扇形ADE中弧DE的长即为圆锥底面圆的周长，即通过计算弧DE的长，再结合圆的周长公式进行计算即可得解.
7.（2017·丽水）如图，点C是以AB为直径的半圆O的三等分点，AC=2，则图中阴影部分的面积是（    ）

A.                           B.                           C.                           D. 
【答案】 A
【考点】扇形面积的计算
【解析】【解答】解：连接OC，∵点C是以AB为直径的半圆O的三等分点，
∴∠ABC=30°，∠BOC=120°，
又∵AB为直径，
∴∠ACB=90°，
则AB=2AC=4，BC= ，
则S阴=S扇形BOC-S△BOC= - = - .
故选A.
【分析】连接OC，S阴=S扇形BOC-S△BOC ， 则需要求出半圆的半径，及圆心角∠BOC；由点C是以AB为直径的半圆O的三等分点，可得∠ABC=30°，∠BOC=120°，从而可解答.
8.（2019·宁波）如图所示，矩形纸片ABCD中，AD=6cm，把它分割成正方形纸片ABFE和矩形纸片EFCD后，分别裁出扇形ABF和半径最大的圆，恰好能作为一个圆锥的侧面和底面，则AB的长为（   ）

A. 3.5cm                                   B. 4cm                                   C. 4.5cm                                   D. 5cm
【答案】 B
【考点】圆锥的计算
【解析】【解答】解：设AB=x，由题意，
得 ，
解得x=4.
故答案为：B。
【分析】设AB=x，根据扇形的弧长计算公式算出弧AF的长，根据该弧长等于直径为（6-x）的圆的周长，列出方程，求解即可。
9.（2020·永州）已知圆锥的底面周长是 分米，母线长为1分米，则圆锥的侧面积是________平方分米．
【答案】
【考点】扇形面积的计算，圆锥的计算
【解析】【解答】根据圆锥的侧面展开图是扇形可知，扇形的弧长等于圆锥底面周长为 分米，扇形的半径等于母线长为1分米，
根据 得， 平方分米．
故答案为 ．
【分析】根据圆锥的侧面展开图就是扇形，求圆锥的侧面积就是求扇形的面积，圆锥的底面周长就是扇形弧长，母线长就是扇形的半径，根据扇形面积公式，即可求解．
10.（2020·宿迁）用半径为4，圆心角为90°的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为________.
【答案】 1
【考点】圆锥的计算
【解析】【解答】解：设这个圆锥的底面圆半径为r，
根据题意得2πr= ，
解得r=1，
所以这个圆锥的底面圆半径为1.
故答案为：1.
【分析】设这个圆锥的底面圆半径为r，利用圆锥的弧长=底面圆的周长，利用弧长公式得到方程并解关于r的方程即可.
11.（2020·黄石）如图，在 的方格纸中，每个小方格都是边长为1的正方形，其中A、B、C为格点，作 的外接圆，则 的长等于________.

【答案】
【考点】弧长的计算
【解析】【解答】解：∵每个小方格都是边长为1的正方形，
∴AB＝2 ，AC＝ ，BC＝ ，
∴AC2＋BC2＝AB2 ，
∴△ACB为等腰直角三角形，
∴∠A＝∠B＝45°，
∴连接OC，则∠COB＝90°，

∵OB＝
∴ 的长为： ＝
故答案为： .
【分析】由AB、BC、AC长可推导出△ACB为等腰直角三角形，连接OC，得出∠BOC＝90°，计算出OB的长就能利用弧长公式求出 的长了.
12.（2020·恩施）如图，已知半圆的直径 ，点C在半圆上，以点A为圆心， 为半径画弧交 于点D，连接 .若 ，则图中阴影部分的面积为________.（结果不取近似值）

【答案】
【考点】扇形面积的计算
【解析】【解答】解：∵AB是直径,
∴∠ACB=90°,∠ABC=60°,
∴BC= ,AC= ,
∴ ,
由以上可知∠CAB=30°,
∴扇形ACD的面积= ,
∴阴影部分的面积为 .
故答案为: .
【分析】根据60°特殊角求出AC和BC,再算出△ABC的面积,根据扇形面积公式求出扇形的面积,再用三角形的面积减去扇形面积即可.
13.（2020·十堰）如图，圆心角为 的扇形 内，以 为直径作半圆，连接 .若阴影部分的面积为 ，则 ________.

【答案】 2
【考点】扇形面积的计算
【解析】【解答】解：将原图区域划分为四部分，阴影部分分别为S1 ， S2；两块空白分别为S3 ， S4 ， 连接DC，如下图所示：

由已知得：三角形ABC为等腰直角三角形，S1+ S2=π-1，
∵BC为直径，
∴∠CDB=90°，即CD⊥AB，
故CD=DB=DA，
∴D点为 中点，由对称性可知 与弦CD围成的面积与S3相等.
设AC=BC=x，
则 ，
其中 ， ，
故： ，
求解得： （舍去）
故答案：2.
【分析】本题可利用扇形面积公式以及三角形面积公式，用大扇形面积减去空白部分面积求得阴影部分面积，继而根据已知列方程求解.
14.（2020·黄冈）如图所示，将一个半径 ，圆心角 的扇形纸板放置在水平面的一条射线 上.在没有滑动的情况下，将扇形 沿射线 翻滚至 再次回到 上时，则半径 的中点P运动的路线长为________ .

【答案】 （）
【考点】弧长的计算
【解析】【解答】解：连接BP，如图，

∵P为AO的中点，AO=10cm，
∴PO=5cm，
由勾股定理得，BP= ，
中点P经过的路线可以分为四段，当弧AB切射线OM于点B时，有OB⊥射线OM，此时P点绕不动点B转过了90°，此时点P经过的路径长为： cm；
第二段：OB⊥射线OM到OA⊥射线OM，P点绕动点转动，而这一过程中弧AB始终是切于射线OM的，所以P与转动点的连线始终⊥射线OM，所以P点过的路线长=AB的弧长，即 ；
第三段：OB⊥射线OM到P点落在射线OM上，P点绕不动点A转过了90°，此时点P经过的路径长为： ；
第四段：OA⊥射线OM到OB与射线OM重合，P点绕不动点O转过了90°，此时点P经过的路径长为： ；
所以，P点经过的路线总长S= .
故答案为： （）
【分析】仔细观察顶点P经过的路线可得，中点P经过的路线可以分为四段，分别求出四段的长，再求出其和即可.
15.（2018·百色）如图，把腰长为8的等腰直角三角板OAB的一直角边OA放在直线1上，按顺时针方向在l上转动两次，使得它的斜边转到l上，则直角边OA两次转动所扫过的面积为________．

【答案】 40π
【考点】扇形面积的计算
【解析】【解答】∵△OAB为腰长为8的等腰直角三角形，∴OA=OB=8，AB=8 ，∴直角边OA两次转动所扫过的面积= π•OA2+ π（AB2﹣OB2）=16π+24π=40π．
故答案为：40π．
【分析】根据题意由直角三角形的性质得出OA=OB=8，AB=8 ， 直角边OA第一次扫过的面积其实质就是圆心角是90°，半径是8的扇形的面积；第二次扫过的面积是就是圆心角是135°的半径分别为8与8 的两个扇形面积差的，根据扇形面积计算方法，算出两次扫过的面积和即可。
模拟预测


1.（2020·荆门模拟）已知一扇形的圆心角为 ，半径为5，则以此扇形为侧面的圆锥的底面圆的周长为（   ）
A.                                       B.                                       C.                                       D. 
【答案】 A
【考点】弧长的计算，圆锥的计算
【解析】【解答】解：扇形的弧长＝ ，
以此扇形为侧面的圆锥的底面圆的周长为 .
故答案为：A.
【分析】利用弧长公式计算出扇形的弧长，以此扇形为侧面的圆锥的底面圆的周长即是扇形的弧长.
2.（2020·鞍山模拟）如图，菱形ABCD中，∠B＝70°，AB＝3，以AD为直径的⊙O交CD于点E，则弧DE的长为（   ）

A.  π                                     B.  π                                     C.  π                                     D.  π
【答案】 A
【考点】弧长的计算
【解析】【解答】连接OE，如图所示：

∵四边形ABCD是菱形，
∴∠D＝∠B＝70°，AD＝AB＝3，
∴OA＝OD＝1.5，
∵OD＝OE，
∴∠OED＝∠D＝70°，
∴∠DOE＝180°﹣2×70°＝40°，
∴ 的长= .
故答案为：:A.
【分析】连接OE，由菱形的性质得出∠D＝∠B＝70°，AD＝AB＝3，得出OA＝OD＝1.5，由等腰三角形的性质和三角形内角和定理求出∠DOE＝40°，再由弧长公式即可得出答案.
3.（2020·镇海模拟）如图，5×3的网格图中，每个小正方形的边长均为1，设经过图中格点A，C，B三点的圆弧与AE交于H，则弧AH的弧长为（   ）

A.  π                              B.  π                              C.  π                              D.  π
【答案】 B
【考点】弧长的计算
【解析】【解答】解：连接EB，BH，AB，

∵BE＝AB＝ ＝ ，AE＝ ＝ ，
∴BE2+AB2＝AE2 ，
∴∠ABE＝90°，
∴△ABE是等腰直角三角形，
∵∠ACB＝90°，
∴AB是圆的直径，
∴∠AHB＝90°，
∴BH⊥AH，
∴∠ABH＝∠BAH＝45°，
∴弧AH所对的圆心角为90°，
∴ 的长＝ ＝ .
故答案为：B.
【分析】连接EB，BH，AB，根据勾股定理得到BE＝AB＝ ＝ ，AE＝ ＝ ，根据勾股定理的逆定理得到△ABE是等腰直角三角形，根据弧长公式即可得到结论.
4.（2020·绵阳模拟）如图，线段EF的长为4，O是EF的中点，以OF为边长做正方形OABC，连接AE、CF交于点P，将正方形OABC从OA与OF重合的位置开始，绕着点O逆时针旋转90°止，则点P运动的路径长为（   ）

A.                                     B.                                     C. 2π                                    D. 
【答案】 B
【考点】弧长的计算
【解析】【解答】解：如图，连接AC．

首先证明∠EPF=135°，推出点P在与K为圆心的圆上，点P的运动轨迹是 ，
在⊙K上取一点M，连接ME、MF、EK、FK，则∠M=180°﹣∠EPF=45°，
推出∠EKF=2∠M=90°，
因为EF=4，
所以KE=KF= ，
根据弧长公式计算可得P运动的路径长= =
故答案为：B．
【分析】连接AC，即可得到∠EPF为135°，根据点P的运动轨迹，在K上取一点M，连接ME、MF、MK、FK，即可得到∠M=180°，∠EPF=45°，推出∠EKF=2∠M=90°，根据弧长公式进行计算即可。
5.（2020·新乡模拟）如图， ， ，以BC为直径作半圆，圆心为点O；以点C为圆心， 为半径作 ，过点O作AC的平行线交两弧于点D、E，则图中阴影部分的面积是（    ）

A.                    B.                    C.                    D. 
【答案】 A
【考点】扇形面积的计算
【解析】【解答】解：如图，连接CE.

∵AC⊥BC，AC＝BC＝8，以BC为直径作半圆，圆心为点O；以点C为圆心，BC为半径作弧AB，
∴∠ACB＝90°，OB＝OC＝OD＝4，BC＝CE＝8.
又∵OE∥AC，
∴∠ACB＝∠COE＝90°.
∴在Rt△OEC中，OC＝4，CE＝8，
∴∠CEO＝30°，∠ECB＝60°，OE＝4 ，
∴S阴影＝S扇形BCE−S扇形BOD−S△OCE
＝
=
故答案为：A.
【分析】如图，连接CE.图中S阴影＝S扇形BCE−S扇形BOD−S△OCE.根据已知条件易求得OB＝OC＝OD＝4，BC＝CE＝8，∠ECB＝60°，OE＝4 ，所以由扇形面积公式、三角形面积公式进行解答即可.
6.（2020·旌阳模拟）已知圆锥的高为 ，母线为 ，且 ，圆锥的侧面展开图为如图所示的扇形．将扇形沿 折叠，使A点恰好落在 上的F点，则弧长 与圆锥的底面周长的比值为（    ）

A.                                          B.                                          C.                                          D. 
【答案】 B
【考点】圆锥的计算
【解析】【解答】连接AF，如图，

设OB=5a，AB=18a，∠BAC=n°
∴ ，
解得n=100
即∠BAC=100°
∵将扇形沿BE折叠，使A点恰好落在 上F点，
∴BA=BF
而AB=AF
∴△ABF为等边三角形
∴∠BAF=60°
∴∠FAC=40°
∴ 的长度=
∴弧长CF与圆锥的底面周长的比值=
故答案为：B
【分析】连接AF，如图，设OB=5a，AB=18a，∠BAC=n°，利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长得到 ，解得n得到∠BAC=100°，再根据折叠的性质得到BA=BF，则可判断△ABF为等边三角形，于是可计算出∠FAC=40°，然后根据弧长公式计算弧长CF与圆锥的底面周长的比值．
7.（2020·阿城模拟）一个扇形的圆心角为 ，面积为 ，则此扇形的半径是________cm.
【答案】 3
【考点】扇形面积的计算
【解析】【解答】解：根据题意得
·π·r2=3π
解得r=3（负值舍去）.
故此扇形的半径为3cm.
【分析】根据扇形的面积公式S扇形=列方程求解即可.
8.（2020·鹿城模拟）某个圆锥的侧面展开图就一个半径为6cm，圆心角为120 的扇形，则这个圆锥底面圆的半径为________
【答案】 2
【考点】圆锥的计算
【解析】【解答】解：∵ 某个圆锥的侧面展开图就一个半径为6cm，圆心角为120 的扇形
∴此扇形的弧长为
∴
解之：r=2.
故答案为：2.
【分析】根据圆锥的侧面展开图的扇形的弧长等于底面圆的周长，建立方程求出结果。
9.（2020·昆明模拟）如图，已知一块圆心角为270°的扇形铁皮，用它做一个圆锥形的烟囱帽（接缝忽略不计），圆锥底面圆的直径是60cm，则这块扇形铁皮的半径是________cm.

【答案】 40
【考点】圆锥的计算
【解析】【解答】解：∵圆锥的底面直径为60cm，
∴圆锥的底面周长为60πcm，
∴扇形的弧长为60πcm，
设扇形的半径为r，
则 =60π，
解得：r=40cm，
故答案为:40cm.
【分析】首先根据圆锥的底面直径求得圆锥的底面周长，然后根据底面周长等于展开扇形的弧长求得铁皮的半径即可.
10.（2020·杭州模拟）如图，在半径为 ，圆心角等于45°的扇形AOB内部作一个矩形CDEF，使点C在OA上，点D、E在OB上，点F在弧AB上，且DE＝2CD，则：

（1）弧AB的长是（结果保留π）________；
（2）图中阴影部分的面积为（结果保留π）________.
【答案】 （1）
（2）
【考点】弧长的计算，扇形面积的计算
【解析】【解答】解：（1）∵n＝45°，r＝ ，
∴l＝ ；
（ 2 ）连接OF，

设CD＝x，则DE＝2x
∵∠O＝45°，则OD＝x，
在直角三角形OEF中，由勾股定理得OE2+EF2＝OF2 ，
即（3x）2+x2＝ ，
解得x＝±1（舍去负数），
∴OD＝1，
S阴影＝S扇形AOB﹣S△OCD﹣S矩形CDFE
＝ .
【分析】（1）利用弧长公式计算即可；
（2）连接OF，设CD＝x，则DE＝2x，OD=x，在直角三角形OEF中，由勾股定理得OE2+EF2＝OF2 ， 从而可得（3x）2+x2＝ ，求出x的值，即得OD=1，利用S阴影＝S扇形AOB﹣S△OCD﹣S矩形CDFE即可求出结论.